- 309.00 KB
- 2021-05-29 发布
2016-2017学年青海师大二附中高二(上)第一次月考数学试卷
一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列说法中正确的是( )
A.棱柱的侧面可以是三角形
B.正方体和长方体都是特殊的四棱柱
C.所有的几何体的表面都能展成平面图形
D.棱柱的各条棱都相等
2.某几何体的三视图,如图所示,则这个几何体是( )
A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱
3.棱长都是1的三棱锥的表面积为( )
A. B. C. D.
4.体积为78的圆台,一个底面积是另一个底面积的9倍,那么截得这个圆台的圆锥的体积是( )
A.54 B.54π C.81 D.81π
5.圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为( )
A.7 B.6 C.5 D.3
6.某几何体的三视图如图所示,则该几何体的体积为( )
A.16+8π B.8+8π C.16+16π D.8+16π
7.在正方体ABCD﹣A1B1C1D1中,若E为A1C1中点,则直线CE垂直于( )
A.AC B.BD C.A1D D.A1A
8.下列命题中,错误的是( )
A.一个平面与两个平行平面相交,交线平行
B.平行于同一个平面的两个平面平行
C.平行于同一条直线的两个平面平行
D.一条直线与两个平行平面中的一个相交,则必与另一个相交
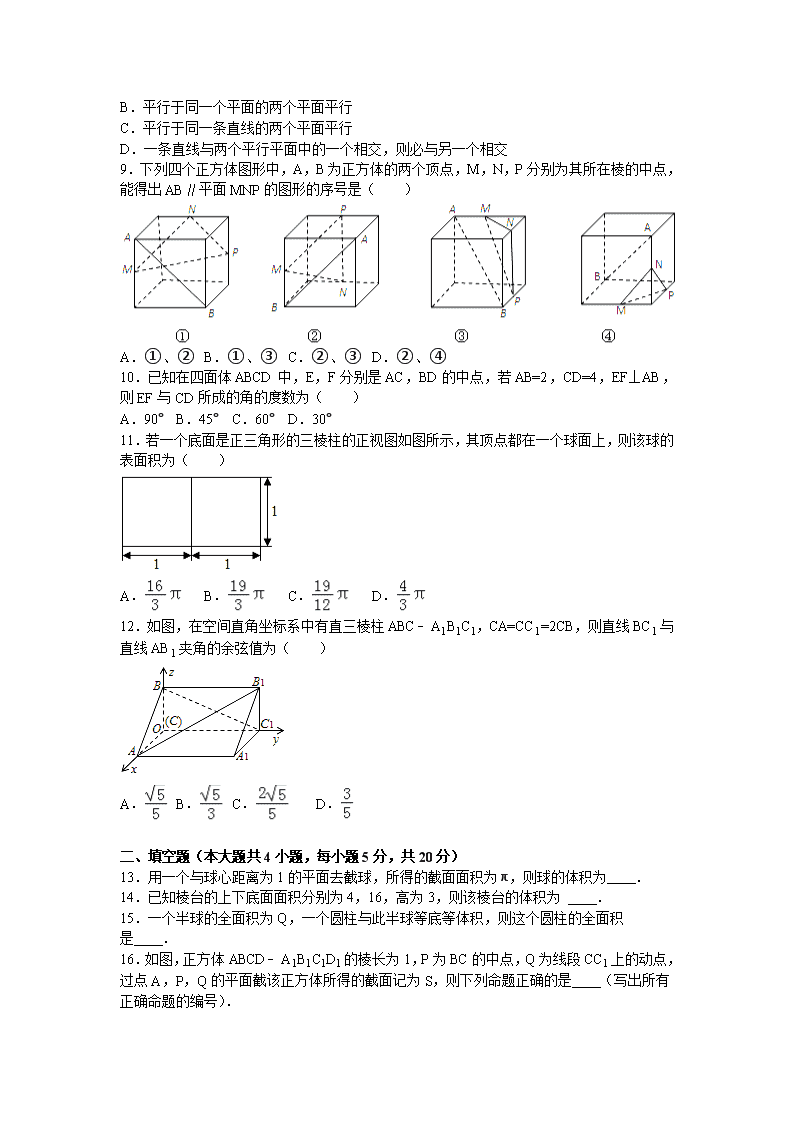
9.下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是( )
A.①、② B.①、③ C.②、③ D.②、④
10.已知在四面体ABCD中,E,F分别是AC,BD的中点,若AB=2,CD=4,EF⊥AB,则EF与CD所成的角的度数为( )
A.90° B.45° C.60° D.30°
11.若一个底面是正三角形的三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为( )
A. B. C. D.
12.如图,在空间直角坐标系中有直三棱柱ABC﹣A1B1C1,CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
13.用一个与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为 .
14.已知棱台的上下底面面积分别为4,16,高为3,则该棱台的体积为 .
15.一个半球的全面积为Q,一个圆柱与此半球等底等体积,则这个圆柱的全面积是 .
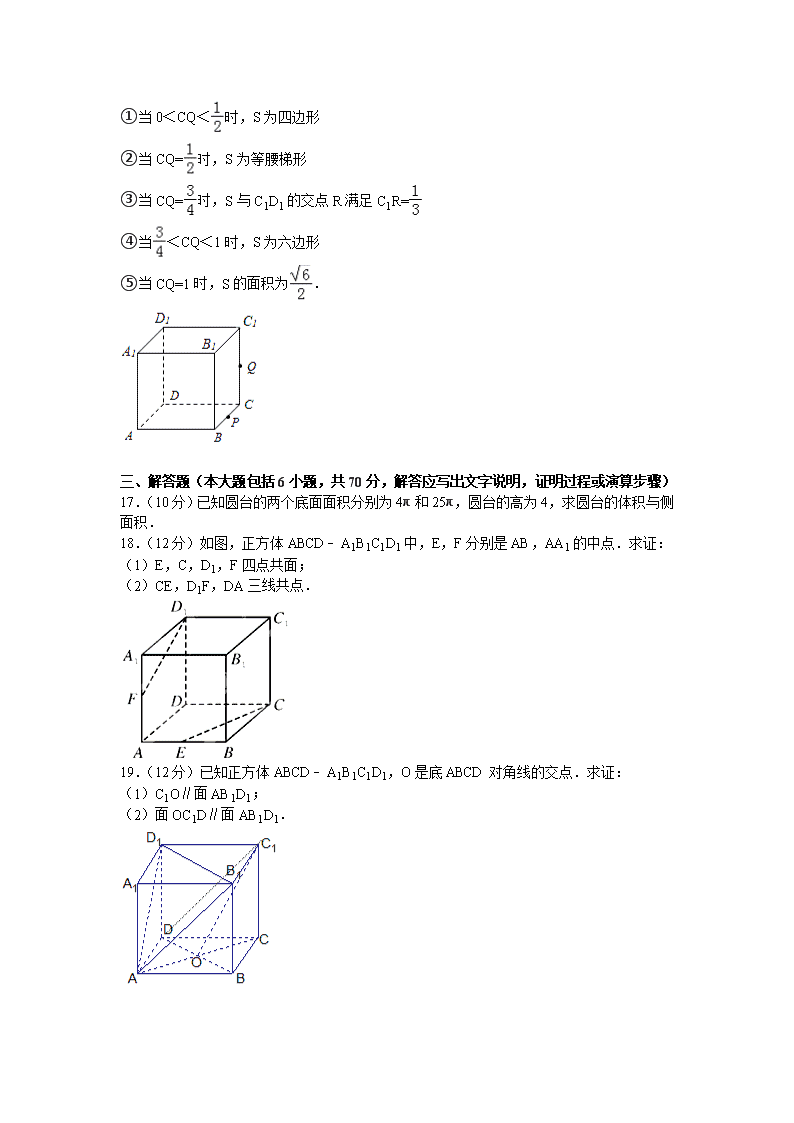
16.如图,正方体ABCD﹣A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是 (写出所有正确命题的编号).
①当0<CQ<时,S为四边形
②当CQ=时,S为等腰梯形
③当CQ=时,S与C1D1的交点R满足C1R=
④当<CQ<1时,S为六边形
⑤当CQ=1时,S的面积为.
三、解答题(本大题包括6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(10分)已知圆台的两个底面面积分别为4π和25π,圆台的高为4,求圆台的体积与侧面积.
18.(12分)如图,正方体ABCD﹣A1B1C1D1中,E,F分别是AB,AA1的中点.求证:
(1)E,C,D1,F四点共面;
(2)CE,D1F,DA三线共点.
19.(12分)已知正方体ABCD﹣A1B1C1D1,O是底ABCD对角线的交点.求证:
(1)C1O∥面AB1D1;
(2)面OC1D∥面AB1D1.
20.(12分)如图,在直三棱柱ABC﹣A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D为AB的中点.
(Ⅰ)求证AC1∥平面CDB1
(Ⅱ)求异面直线AC1与B1C所成角的余弦值.
21.(12分)在正方体ABCD﹣A1B1C1D1中,G是C1D1的中点,H是A1B1的中点
(1)求异面直线AH与BC1所成角的余弦值;
(2)求证:BC1∥平面B1DG.
22.(12分)如图,正方体ABCD﹣A′B′C′D′的棱长为a,连接A′C′,A′D,A′B,BD,BC′,C′D,得到一个三棱锥.求:
(1)三棱锥A′﹣BC′D的体积.
(2)若球O1使得其与三棱锥A′﹣BC′D的六条棱都相切,三棱锥A′﹣BC′D外接球为O2,内切球为O3,求球O1,O2,O3半径的比值.
2016-2017学年青海师大二附中高二(上)第一次月考数学试卷
参考答案与试题解析
一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2016秋•城东区校级月考)下列说法中正确的是( )
A.棱柱的侧面可以是三角形
B.正方体和长方体都是特殊的四棱柱
C.所有的几何体的表面都能展成平面图形
D.棱柱的各条棱都相等
【考点】棱柱的结构特征.
【专题】阅读型.
【分析】从棱柱的定义出发判断A、B、D的正误,找出反例否定C,即可推出结果.
【解答】解:棱柱的侧面都是四边形,A不正确;
正方体和长方体都是特殊的四棱柱,正确;
所有的几何体的表面都能展成平面图形,球不能展开为平面图形,C不正确;
棱柱的各条棱都相等,应该为侧棱相等,所以D不正确;
故选B
【点评】本题考查棱柱的结构特征,考查基本知识的熟练情况,是基础题.
2.(2015秋•岳阳校级期末)某几何体的三视图,如图所示,则这个几何体是( )
A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱
【考点】简单空间图形的三视图.
【专题】空间位置关系与距离.
【分析】根据几何体的三视图,得出该几何体是什么图形.
【解答】解:根据该几何体的三视图,得出该几何体是平放的三棱柱,如图所示;
故选:B.
【点评】本题考查了空间几何体的三视图的应用问题,解题时应根据几何体的三视图,得出几何体表示什么图形,是基础题.
3.(2014秋•元宝山区期末)棱长都是1的三棱锥的表面积为( )
A. B. C. D.
【考点】棱柱、棱锥、棱台的侧面积和表面积.
【专题】计算题.
【分析】棱长都是1的三棱锥,四个面是全等的正三角形,求出一个面积即可求得结果.
【解答】解:因为四个面是全等的正三角形,
则.
故选A
【点评】本题考查棱锥的面积,是基础题.
4.(2016秋•城东区校级月考)体积为78的圆台,一个底面积是另一个底面积的9倍,那么截得这个圆台的圆锥的体积是( )
A.54 B.54π C.81 D.81π
【考点】旋转体(圆柱、圆锥、圆台).
【专题】转化思想;空间位置关系与距离.
【分析】设截得这个圆台的圆锥的体积是V.设两个底面半径分别为:r,R,则=,解得.再利用=,即可得出.
【解答】解:设截得这个圆台的圆锥的体积是V.
设两个底面半径分别为:r,R,则=,解得=.
∴==,
解得V=81.
故选:C.
【点评】本题考查了圆台的体积计算公式及其性质、相似三角形的性质、圆的面积,考查了推理能力与计算能力,属于中档题.
5.(2013•宣武区校级模拟)圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为( )
A.7 B.6 C.5 D.3
【考点】旋转体(圆柱、圆锥、圆台).
【专题】计算题.
【分析】设出上底面半径为r,利用圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,求出上底面半径,即可.
【解答】解:设上底面半径为r,因为圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,所以S侧面积=π(r+3r)l=84π,r=7
故选A
【点评】本题是基础题,考查 圆台的侧面积公式,考查计算能力,送分题.
6.(2016•衡水模拟)某几何体的三视图如图所示,则该几何体的体积为( )
A.16+8π B.8+8π C.16+16π D.8+16π
【考点】由三视图求面积、体积.
【专题】空间位置关系与距离.
【分析】根据几何体的三视图,得出该几何体是下面为半圆柱,上面为长方体的组合体,由此求出它的体积.
【解答】解:根据几何体的三视图,得;
该几何体是下面为半圆柱,上面为长方体的组合体,
半圆柱的底面半径为2,高为4,
∴半圆柱的体积为:×π•22×4=8π;
长方体的长宽高分别为4,2,2,
∴长方体的体积为4×2×2=16,
∴该几何体的体积为V=16+8π.
故选:A.
【点评】本题考查了空间几何体的三视图的应用问题,解题时应根据几何体的三视图得出该几何体的结构特征,是基础题目.
7.(2012•北京模拟)在正方体ABCD﹣A1B1C1D1中,若E为A1C1中点,则直线CE垂直于( )
A.AC B.BD C.A1D D.A1A
【考点】向量语言表述线线的垂直、平行关系.
【专题】向量法.
【分析】建立空间直角坐标系,设正方体棱长为1,求出向量的坐标,以及、、 的坐标,可以发现 •=0,因此,⊥,即CE⊥BD.
【解答】解:以A为原点,AB、AD、AA1所在直线分别为x,y,z轴建空间直角坐标系,设正方体棱长为1,
则A(0,0,0),C(1,1,0),B(1,0,0),
D(0,1,0),A1(0,0,1),E(,,1),
∴=(﹣,﹣,1),
=(1,1,0),=(﹣1,1,0),
=(0,1,﹣1),=(0,0,﹣1),
显然•=﹣+0=0,
∴⊥,即CE⊥BD.
故选:B.
【点评】本题考查利用空间直角坐标系求向量的坐标,再利用2个向量的数量级等于0,证明两个向量垂直,属于中档题.
8.(2016秋•城东区校级月考)下列命题中,错误的是( )
A.一个平面与两个平行平面相交,交线平行
B.平行于同一个平面的两个平面平行
C.平行于同一条直线的两个平面平行
D.一条直线与两个平行平面中的一个相交,则必与另一个相交
【考点】四种命题.
【专题】空间位置关系与距离.
【分析】根据空间中的直线与直线、直线与平面以及平面与平面的平行关系,对每一个命题进行判断即可.
【解答】解:对于A,一个平面与两个平面相交,它们的交线平行,是正确的;
对于B,平行于同一个平面的两个平面互相平行,是正确的;
对于C,平行于同一条直线的两个平面不一定平行,是错误的,
如竖直的旗杆与所有竖直的墙面是平行的,但所有竖直的墙面并不一定平行;
对于D,一条直线与两个平行平面中的一个相交,则必与另一个相交,是正确的.
故选:C.
【点评】本题考查了空间中的平行关系的应用问题,解题时应明确空间中的线线、线面以及面面之间的平行关系,是基础题.
9.(2012春•黄州区校级期末)下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是( )
A.①、② B.①、③ C.②、③ D.②、④
【考点】直线与平面平行的判定.
【专题】空间位置关系与距离.
【分析】分别利用线面平行的判定定理,在平面MNP中能否寻找一条直线和AB平行即可.
【解答】解:在①中NP平行所在正方体的那个侧面的对角线,从而平行AB,所以AB∥平面MNP;
在③中设过点B且垂直于上底面的棱与上底面交点为C,
则由NP∥CB,MN∥AC可知平面MNP∥平行平面ABC,
即AB∥平面MNP.
故选B.
【点评】本题主要考查线面平行的判定,利用线面平行的判定,只要直线AB平行于平面MNP内的一条直线即可.
10.(2016春•牡丹江校级期末)已知在四面体ABCD中,E,F分别是AC,BD的中点,若AB=2,CD=4,EF⊥AB,则EF与CD所成的角的度数为( )
A.90° B.45° C.60° D.30°
【考点】异面直线及其所成的角.
【专题】空间角.
【分析】设G为AD的中点,连接GF,GE,利用三角形中位线定理,可证出EF⊥GF且∠FEG或其补角即为EF与CD所成角.最后在Rt△EFG中,利用正弦的定义算出∠GEF=30°,即得EF与CD所成的角的度数.
【解答】解:设G为AD的中点,连接GF,GE,
则GF,GE分别为△ABD,△ACD的中线.
由此可得,GF∥AB且GF=AB=1,
GE∥CD,且GE=CD=2,
∴∠FEG或其补角即为EF与CD所成角.
又∵EF⊥AB,GF∥AB,∴EF⊥GF
因此,Rt△EFG中,GF=1,GE=2,
由正弦的定义,得sin∠GEF==,可得∠GEF=30°.
∴EF与CD所成的角的度数为30°
故选:D
【点评】本题给出空间四边形相对的棱长,在已知对角线的中点连线与一条棱垂直的情况下求异面直线所成的角,着重考查了是异面直线所成的定义及其求法等知识,属于中档题.本题利用三角形中位线定理,平行线的性质是解决问题的关键.
11.(2014•赣州二模)若一个底面是正三角形的三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为( )
A. B. C. D.
【考点】由三视图求面积、体积.
【专题】计算题.
【分析】根据由已知底面是正三角形的三棱柱的正视图,我们可得该三棱柱的底面棱长为2,高为1,进而求出底面外接圆半径r,球心到底面的球心距d,球半径R,代入球的表面积公式.即可求出球的表面积.
【解答】解:由已知底面是正三角形的三棱柱的正视图
我们可得该三棱柱的底面棱长为2,高为1
则底面外接圆半径r=,球心到底面的球心距d=
则球半径R2==
则该球的表面积S=4πR2=
故选B
【点评】本题考查的知识点是由三视图求表面积,其中根据截面圆半径、球心距、球半径满足勾股定理计算球的半径,是解答本题的关键.
12.(2012•陕西)如图,在空间直角坐标系中有直三棱柱ABC﹣A1B1C1,CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为( )
A. B. C. D.
【考点】异面直线及其所成的角.
【专题】计算题.
【分析】根据题意可设CB=1,CA=CC1=2,分别以CA、CC1、CB为x轴、y轴和z轴建立如图坐标系,得到A、B、B1、C1四个点的坐标,从而得到向量与的坐标,根据异面直线所成的角的定义,结合空间两个向量数量积的坐标公式,可以算出直线BC1与直线AB1夹角的余弦值.
【解答】解:分别以CA、CC1、CB为x轴、y轴和z轴建立如图坐标系,
∵CA=CC1=2CB,∴可设CB=1,CA=CC1=2
∴A(2,0,0),B(0,0,1),B1(0,2,1),C1(0,2,0)
∴=(0,2,﹣1),=(﹣2,2,1)
可得•=0×(﹣2)+2×2+(﹣1)×1=3,且=,=3,
向量与所成的角(或其补角)就是直线BC1与直线AB1夹角,
设直线BC1与直线AB1夹角为θ,则cosθ==
故选A
【点评】本题给出一个特殊的直三棱柱,求位于两个侧面的面对角线所成角的余弦之值,着重考查了空间向量的坐标运算和异面直线及其所成的角的概论,属于基础题.
二、填空题(本大题共4小题,每小题5分,共20分)
13.(2012•上海二模)用一个与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为 π .
【考点】球的体积和表面积.
【专题】计算题.
【分析】求出小圆的半径,利用球心到该截面的距离为1 cm,小圆的半径,通过勾股定理求出球的半径,即可求出球的体积.
【解答】解:用一平面去截球所得截面的面积为π,所以小圆的半径为1
已知球心到该截面的距离为1,所以球的半径为r==
所以球的体积为:πr3=π
故答案为:π
【点评】本题考查球的小圆的半径,球心到该截面的距离,球的半径之间的关系,考查计算能力,是基础题.
14.(2013秋•聊城期末)已知棱台的上下底面面积分别为4,16,高为3,则该棱台的体积为 28 .
【考点】棱柱、棱锥、棱台的体积.
【专题】计算题.
【分析】直接利用棱台的体积公式,求出棱台的体积.
【解答】解:
故答案为:28.
【点评】本题考查棱台的体积,考查计算能力,是基础题.
15.(2016秋•城东区校级月考)一个半球的全面积为Q,一个圆柱与此半球等底等体积,则这个圆柱的全面积是 Q .
【考点】棱柱、棱锥、棱台的侧面积和表面积;球的体积和表面积.
【专题】计算题.
【分析】由半球的全面积求出半径,再根据一个圆柱与此半球等底等体积,可求出圆柱的高,代入圆柱的全面积进行运算.
【解答】解:半球的全面积 ,
故答案为 Q.
【点评】本题考查半球的表面积、体积的求法,圆柱的体积、全面积的求法.
16.(2013•安徽)如图,正方体ABCD﹣A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是 ①②③⑤ (写出所有正确命题的编号).
①当0<CQ<时,S为四边形
②当CQ=时,S为等腰梯形
③当CQ=时,S与C1D1的交点R满足C1R=
④当<CQ<1时,S为六边形
⑤当CQ=1时,S的面积为.
【考点】命题的真假判断与应用.
【专题】空间位置关系与距离;简易逻辑.
【分析】由题意作出满足条件的图形,由线面位置关系找出截面可判断选项的正误.
【解答】解:如图
当CQ=时,即Q为CC1中点,此时可得PQ∥AD1,AP=QD1==,
故可得截面APQD1为等腰梯形,故②正确;
由上图当点Q向C移动时,满足0<CQ<,只需在DD1上取点M满足AM∥PQ,
即可得截面为四边形APQM,故①正确;
③当CQ=时,如图,
延长DD1至N,使D1N=,连接AN交A1D1于S,连接NQ交C1D1于R,连接SR,
可证AN∥PQ,由△NRD1∽△QRC1,可得C1R:D1R=C1Q:D1N=1:2,故可得C1R=,故正确;
④由③可知当<CQ<1时,只需点Q上移即可,此时的截面形状仍然上图所示的APQRS,显然为五边形,故错误;
⑤当CQ=1时,Q与C1重合,取A1D1的中点F,连接AF,可证PC1∥AF,且PC1=AF,
可知截面为APC1F为菱形,故其面积为AC1•PF==,故正确.
故答案为:①②③⑤.
【点评】本题考查命题真假的判断与应用,涉及正方体的截面问题,属中档题.
三、解答题(本大题包括6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(10分)(2016秋•城东区校级月考)已知圆台的两个底面面积分别为4π和25π,圆台的高为4,求圆台的体积与侧面积.
【考点】棱柱、棱锥、棱台的体积;旋转体(圆柱、圆锥、圆台);棱柱、棱锥、棱台的侧面积和表面积.
【专题】对应思想;综合法;立体几何.
【分析】求出圆台的上下底面半径和母线长,代入侧面积各体积公式计算即可.
【解答】解:圆台的体积V=(4π+25π+)•4=42π.
圆台的上下底面半径分别为r=2,R=5,
∴圆台的母线长为l==5,
∴圆台的侧面积S侧=πrl+πRl=10π+25π=35π.
【点评】本题考查了旋转体的结构特征,体积与侧面积计算,属于中档题.
18.(12分)(2015秋•蒙城县校级期末)如图,正方体ABCD﹣A1B1C1D1中,E,F分别是AB,AA1的中点.求证:
(1)E,C,D1,F四点共面;
(2)CE,D1F,DA三线共点.
【考点】平面的基本性质及推论.
【专题】计算题;空间位置关系与距离.
【分析】(1)由三角形中位线定理和平行公式,得到EF∥D1C,再由两条平行线确定一个平面,得到E,C,D1,F四点共面.
(2)分别延长D1F,DA,交于点P,由P∈DA,DA⊂面ABCD,知P∈面ABCD.再由三角形中位线定理证明CE,D1F,DA三线共点于P.
【解答】证明:(1)连接EF,A1B,D1C,
∵E,F分别是AB,AA1的中点,
∴EF∥A1B,A1B∥D1C,
∴EF∥D1C,
∴由两条平行线确定一个平面,得到E,C,D1,F四点共面.
(2)分别延长D1F,DA,交于点P,
∵P∈DA,DA⊂面ABCD,
∴P∈面ABCD.
∵F是AA1的中点,FA∥D1D,
∴A是DP的中点,
连接CP,∵AB∥DC,
∴CP∩AB=E,
∴CE,D1F,DA三线共点于P.
【点评】本题考查四点共面和三点共线的证明,解题时要认真审题,仔细解答,注意平行公理和三角形中位线定理的合理运用.
19.(12分)(2016秋•镜湖区校级期中)已知正方体ABCD﹣A1B1C1D1,O是底ABCD对角线的交点.求证:
(1)C1O∥面AB1D1;
(2)面OC1D∥面AB1D1.
【考点】平面与平面平行的判定;直线与平面平行的判定.
【专题】作图题;证明题;转化思想;空间位置关系与距离.
【分析】(1)线面平行,只需要证明线线平行.连接A1C1交于O1.连接AO1只需要证明AO1∥C1O即可.
(2)面面平行,只需要证明一个平面内条的两条相交直线与平面平行即可,B1D1∥BD,AO1∥C1O,
BD∩C1O=O,那么可证得面OC1D∥面AB1D1.
【解答】解:(1)由题意:几何体ABCD﹣A1B1C1D1是正方体,O是底ABCD对角线的交点,
∴B1D1∥BD,
连接A1C1交于O1,连接AO1,
C1O1
∴C1O1AO是平行四边形.
∴AO1∥C1O.
∵AO1⊂面AB1D1;
∴C1O∥面AB1D1;
得证.
(2).∵B1D1∥BD,即OD∥B1D1,
OD⊂面OC1D,
∴OD∥面AB1D1.
由(1)可得C1O∥面AB1D1;
OD∩C1O=O,
所以:面OC1D∥面AB1D1.
【点评】本题考查了线面平行和面面平行的证明.线面平行转化为线线平行;面面平行转化为线面平行.属于基础题.
20.(12分)(2013秋•肇庆期末)如图,在直三棱柱ABC﹣A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D为AB的中点.
(Ⅰ)求证AC1∥平面CDB1
(Ⅱ)求异面直线AC1与B1C所成角的余弦值.
【考点】直线与平面平行的判定;异面直线及其所成的角.
【专题】计算题;空间角.
【分析】(I)由OD是△ABC1的中位线,得OD∥AC1,再由线面平行的判定定理证明.
(II)根据异面直线所成角的定义,判断∠COD为异面直线所成的角,利用余弦定理求解.
【解答】解:(I)证明:记BC1与CB1交于点O,连OD
∵OD是△ABC1的中位线,∴OD∥AC1
∵AC1⊄面CDB1OD⊂面CDB1
∴AC1∥平面CDB1;
(II)由(I)知OD∥AC1
∴∠COD为异面直线AC1与B1C所成的角,
∵在Rt△ACC1中,AC=3,CC1=4∴AC1=5∴OD=,
在正方形CBB1C1中,B1C=4,∴OC=2,
∵AC=3,BC=4,AB=5,∴AC⊥BC,∴CD==,
在△COD中,cos∠COD==.
【点评】本题考查了线面平行的证明,考查了求异面直线所成的角,考查学生的空间想象能力与运算能力.
21.(12分)(2016秋•城东区校级月考)在正方体ABCD﹣A1B1C1D1中,G是C1D1的中点,H是A1B1的中点
(1)求异面直线AH与BC1所成角的余弦值;
(2)求证:BC1∥平面B1DG.
【考点】异面直线及其所成的角;直线与平面平行的判定.
【专题】空间位置关系与距离;空间角.
【分析】(1)连结AD1,HD1,说明∠D1AH为异面直线AH与BC1所所成的角,在△AD1H中,求解cos∠D1AH的值即可.
(2)证明:连结BD1交B1D于点O,连结OG,证明OG∥BC1,然后证明BC1∥平面B1DG
【解答】解:(1)连结AD1,HD1,
∵AB∥C1D1 AB=C1D1
∴四边形ABC1D1为平行四边形,
∴AD1∥BC1,
∴∠D1AH为异面直线AH与BC1所所成的角,….….(2分)
设正方体棱长为1,
在△AD1H中,AD1=,AH=D1H=,
∴cos∠D1AH== …..….
∴异面直线AH与BC1所成角的余弦值为 ….(6分)
(2)证明:连结BD1交B1D于点O,
连结OG,易知O为BD1的中点,
在△BC1D1中,OG为中位线,∴OG∥BC1
又OG⊂平面B1DG且SC1⊄平面B1DG,
∴BC1∥平面B1DG ….(12分)
【点评】本题考查直线与平面平行的判定定理以及异面直线所成角的求法,考查计算能力.
22.(12分)(2016秋•城东区校级月考)如图,正方体ABCD﹣A′B′C′D′的棱长为a,连接A′C′,A′D,A′B,BD,BC′,C′D,得到一个三棱锥.求:
(1)三棱锥A′﹣BC′D的体积.
(2)若球O1使得其与三棱锥A′﹣BC′D的六条棱都相切,三棱锥A′﹣BC′D外接球为O2,内切球为O3,求球O1,O2,O3半径的比值.
【考点】棱柱、棱锥、棱台的体积;球内接多面体.
【专题】综合题;转化思想;演绎法;空间位置关系与距离.
【分析】(1)利用割补法,求三棱锥A′﹣BC′D的体积.
(2)分别求出球O1,O2,O3半径,即可求球O1,O2,O3半径的比值.
【解答】解:(1)三棱锥A′﹣BC′D的体积=a3﹣4×=;
(2)设三棱锥A′﹣BC′D的六条棱长为1个单位,则棱锥的高为,O2,O3半径为,,O2与O3半径比为3:1,
三棱锥对棱的距离为=,所以球O1半径为,
∴球O1,O2,O3半径的比值为:3:1.
【点评】本题考查体积的计算,考查学生的计算能力,正确计算是关键.