2020学年度九年级数学上册 21.2.4解一元二次方程-因式分解法 5页

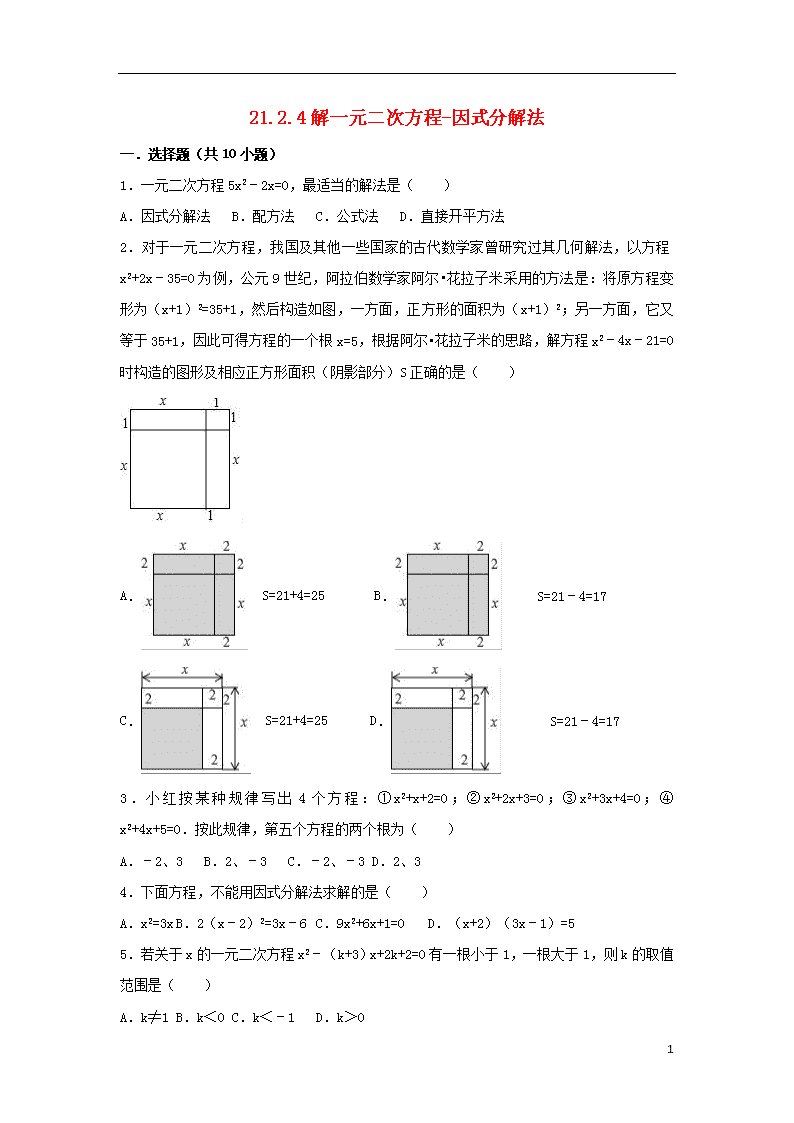
‎21.2.4‎解一元二次方程-因式分解法 一．选择题（共10小题）‎ ‎1．一元二次方程5x2﹣2x=0，最适当的解法是（　　）‎ A．因式分解法 B．配方法 C．公式法 D．直接开平方法 ‎2．对于一元二次方程，我国及其他一些国家的古代数学家曾研究过其几何解法，以方程x2+2x﹣35=0为例，公元9世纪，阿拉伯数学家阿尔•花拉子米采用的方法是：将原方程变形为（x+1）2=35+1，然后构造如图，一方面，正方形的面积为（x+1）2；另一方面，它又等于35+1，因此可得方程的一个根x=5，根据阿尔•花拉子米的思路，解方程x2﹣4x﹣21=0时构造的图形及相应正方形面积（阴影部分）S正确的是（　　）‎ A． S=21+4=25 B． S=21﹣4=17‎ C． S=21+4=25 D． S=21﹣4=17‎ ‎3．小红按某种规律写出4个方程：①x2+x+2=0；②x2+2x+3=0；③x2+3x+4=0；④x2+4x+5=0．按此规律，第五个方程的两个根为（　　）‎ A．﹣2、3 B．2、﹣‎3 ‎C．﹣2、﹣3 D．2、3‎ ‎4．下面方程，不能用因式分解法求解的是（　　）‎ A．x2=3x B．2（x﹣2）2=3x﹣‎6 ‎C．9x2+6x+1=0 D．（x+2）（3x﹣1）=5‎ ‎5．若关于x的一元二次方程x2﹣（k+3）x+2k+2=0有一根小于1，一根大于1，则k的取值范围是（　　）‎ A．k≠1 B．k＜‎0 ‎C．k＜﹣1 D．k＞0‎ 5‎ ‎6．方程（x﹣）2+（x﹣）（x﹣）=0的较小的根为（　　）‎ A．﹣ B． C． D．‎ ‎7．已知方程（x+m）（x﹣4）=0和方程x2﹣2x﹣8=0的两根分别相等，则m等于（　　）‎ A．1 B．﹣‎1 ‎C．2 D．﹣2‎ ‎8．一个等腰三角形的两条边长分别是方程x2﹣7x+10=0的两根，则该等腰三角形的周长是（　　）‎ A．12 B．‎9 ‎C．13 D．12或9‎ ‎9．已知三角形的两边长为4和5，第三边的长是方程x2﹣5x+6=0的一个根，则这个三角形的周长是（　　）‎ A．11 B．‎12 ‎C．11或12 D．15‎ ‎10．已知关于x的方程x2﹣px+q=0的两个根是x1=1，x2=﹣2．则二次三项式x2﹣px+q可以分解为（　　）‎ A．（x﹣1）（x+2） B．（x﹣1）（x﹣2） C．（x+1）（x﹣2） D．（x+1）（x+2）‎ ‎　‎ 二．填空题（共5小题）‎ ‎11．已知：a2+b2=1，a+b=，且b＜0，那么a：b=　 　．‎ ‎12．若6x2+7xy﹣5y2=0（y≠0），则=　 　．‎ ‎13．观察下面的表格，探究其中的规律并填空：‎ 一元二次方程 方程的两个根 二次三项式分解因式 x2﹣x﹣2=0‎ x1=﹣1，x2=2‎ x2﹣x﹣2=（x+1）（x﹣2）‎ x2+3x﹣4=0‎ x1=1，x2=﹣4‎ x2+3x﹣4=（x﹣1）（x+4）‎ ‎3x2+x﹣2=0‎ x1=，x2=﹣1‎ ‎3x2+x﹣2=‎ ‎4x2+9x+2=0‎ x1=﹣，x2=﹣2‎ ‎4x2+9x+2=4（x　 　）（x　 　）‎ ‎2x2﹣7x+3=0‎ x1=　 　，x2=　 　‎ ‎2x2﹣7x+3=　 　‎ ax2+bx+c=0‎ x1=m，x2=n ax2+bx+c=　 　‎ ‎14．对于实数a，b，定义运算“※”如下：a※b=a2﹣ab，例如，5※3=52﹣5×3=10．若（x+1）※（x﹣2）=6，则x的值为　 　．‎ 5‎ ‎15．等腰三角形的腰和底边的长是方程x2﹣20x+91=0的两个根，则此三角形的周长为　 　．‎ ‎　‎ 三．解答题（共3小题）‎ ‎16．用适当的方法解方程：x2﹣5x﹣14=0．‎ ‎17．解方程：‎ ‎（1）（x﹣5）2=16（直接开平方法） ‎ ‎（2）x2+8x﹣9=0（配方法）‎ ‎（3）2x2﹣4x﹣5=0（公式法）‎ ‎（4）2x2+10x=0 （因式分解法）‎ ‎18．x2+ax+b分解因式的结果是（x﹣1）（x+2），则方程x2+ax+b=0的二根分别是什么？‎ ‎　‎ 5‎ 参考答案 ‎　‎ 一．选择题（共10小题）‎ ‎1．A．2．C．3．C．4．D．5．B．6．C．7．C．8．A．9．C．10．A．‎ ‎　‎ 二．填空题（共5小题）‎ ‎11．﹣．‎ ‎12．，﹣．‎ ‎13．‎ 一元二次方程 方程的两个根 二次三项式分解因式 x2﹣x﹣2=0‎ x1=﹣1，x2=2‎ x2﹣x﹣2=（x+1）（x﹣2）‎ x2+3x﹣4=0‎ x1=1，x2=﹣4‎ x2+3x﹣4=（x﹣1）（x+4）‎ ‎3x2+x﹣2=0‎ x1=，x2=﹣1‎ ‎3x2+x﹣2=‎ ‎4x2+9x+2=0‎ x1=﹣，x2=﹣2‎ ‎4x2+9x+2=4（x+）（x+2）‎ ‎2x2﹣7x+3=0‎ x1=，x2=3‎ ‎2x2﹣7x+3=2（x﹣）（x﹣3）‎ ax2+bx+c=0‎ x1=m，x2=n ax2+bx+c=a（x﹣m）（x﹣n）‎ ‎14．1．‎ ‎15．33或27．‎ ‎　‎ 三．解答题（共3小题）‎ ‎16．解：x2﹣5x﹣14=0‎ ‎（x﹣7）（x+2）=0‎ ‎∴x﹣7=0，x+2=0，‎ 解得，x1=7，x2=﹣2．‎ ‎　‎ ‎17．解：（1）x﹣5=±4，‎ 所以x1=1，x2=9；‎ 5‎ ‎（2）x2+8x=9，‎ x2+8x+16=25，‎ ‎（x+4）2=25，‎ x+4=±5，‎ 所以x1=1，x2=﹣9；‎ ‎（3）△=（﹣4）2﹣4×2×（﹣5）=56，‎ x=，‎ 所以x1=，x2=；‎ ‎（4）2x（x+5）=0，‎ ‎2x=0或x+5=0，‎ 所以x1=0，x2=﹣5．‎ ‎　‎ ‎18．解：∵x2+ax+b=（x﹣1）（x+2），‎ ‎∴x2+ax+b=0可化为：（x﹣1）（x+2）=0，‎ ‎∴x1=l，x2=﹣2．‎ 故两个根分别是：1，﹣2．‎ ‎　‎ 5‎