- 760.50 KB
- 2021-05-28 发布
大庆实验中学2018-2019学年度下学期开学考试
高二 数学(文)试题
第Ⅰ卷(选择题 共60分)
一.选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,则( )
A. B. C. D.
2.若复数满足,则的虚部为( )
A. B. C. D.
3.下列函数中,既是偶函数又在区间上单调递减的是( )
A. B. C. D.
4.命题“”的否定是( )
A. B.
C. D.
5.一组数据从小到大的顺序排列为,其中,已知该组数据的中位数是众数的倍,则该组数据的平均数为( )
A. B. C. D.
6.设是空间两条直线,是空间两个平面,则下列命题中不正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
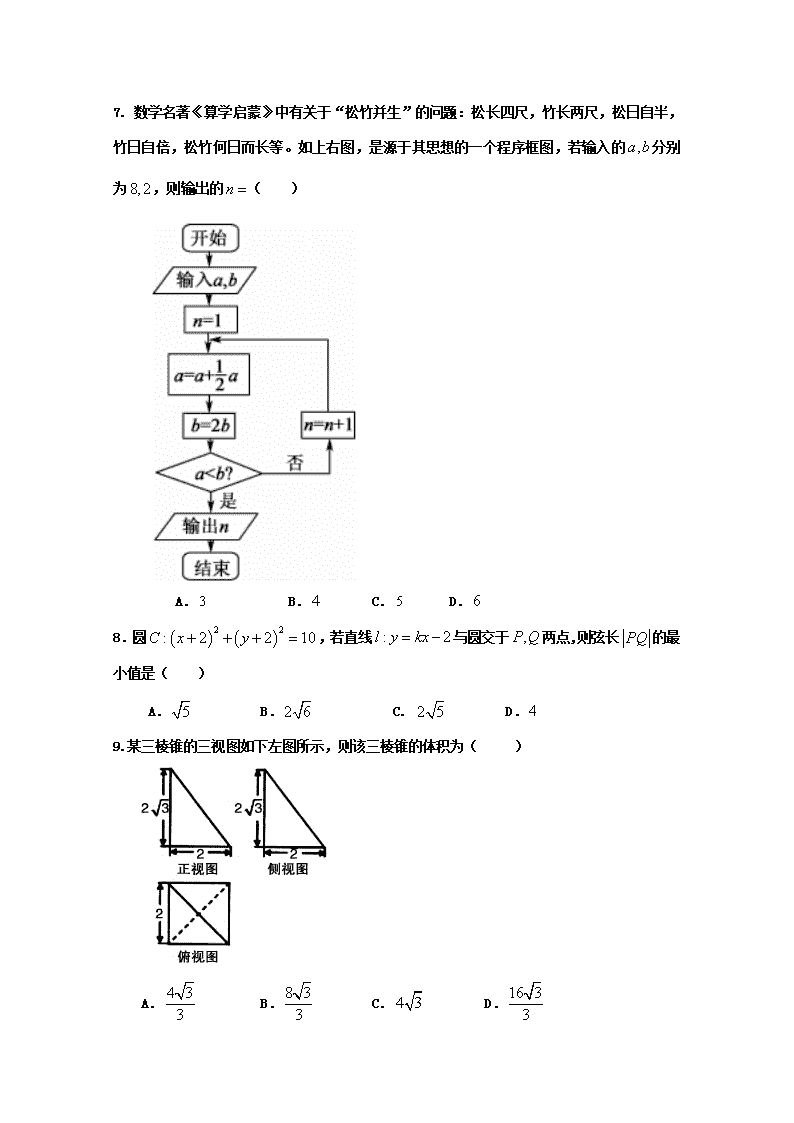
7. 数学名著《算学启蒙》中有关于“松竹并生”的问题:松长四尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等。如上右图,是源于其思想的一个程序框图,若输入的分别为,则输出的( )
A. B. C. D.
8.圆,若直线与圆交于两点,则弦长的最小值是( )
A. B. C. D.
9.某三棱锥的三视图如下左图所示,则该三棱锥的体积为( )
A. B. C. D.
10. 下列说法正确的是( )
A.是的充分不必要条件
B.命题的否定是
C.命题的逆命题为真命题
D.命题为真命题
11、某图书出版公司到实验中学开展奉献爱心图书捐赠活动,某班级获得了某一品牌的图书共四本,其中数学、英语、物理、化学各一本,现将这4本书随机发给该班的甲、乙、丙、丁四个人,每人一本,并请这四个人在看自己得到的赠书之前进行预测,结果如下:
甲说:乙或丙得到物理书;
乙说:甲或丙得到英语书;
丙说:数学书被甲得到;
丁说:甲得到物理书。
最终结果显示:甲、乙、丙、丁四个人的预测均不正确,那么甲、乙、丙、丁四个人得到的书分别为( )
A.化学、英语、数学、物理 B.英语、化学、数学、物理
C. 化学、英语、物理、数学 D.数学、英语、化学、物理
12. 过抛物线的焦点作斜率大于的直线交抛物线于两点(在的上方),且与准线交于点,若,则( )
A. B. C. D.
第Ⅱ卷(非选择题 共90分)
二.填空题:本题共4小题,每小题5分,共20分.
13.已知为虚数单位,则复数的模为 .
14.某校高一年级有个学生,高二年级有个学生,高三年级有个学生,采用分层抽样抽一个容量为的样本,高一年级被抽取人,高二年级被抽取人,则此学校共有学生 人.
15.在实验中学文科数学组微信群的一次抢红包活动中,所发红包的总金额为元,被随机分配为共个红包,由甲和乙等位教师抢,每人只能抢一次,则甲和乙两人抢到的金额之和不低于元的概率是 (用分数表示)
16.设分别为双曲线的左、右焦点,点是双曲线左支上一点,是线段的中点,且,,则双曲线的离心率为 .
三.解答题:本题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分10分)
设为等差数列的前项和,已知.
(1)求数列的通项公式; (2)求,并求的最小值.
18.(本小题满分12分)
已知函数.
(1)求的最小正周期及单调递增区间; (2)当时,求的值域.
19.(本小题满分12分)
设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份
2012
2013
2014
2015
2016
2017
时间代号
1
2
3
4
5
6
储蓄存款(千亿元)
3.5
5
6
7
8
9.5
(1)求关于的回归方程,(请用最简分数作答);
(2)请用所学知识分析2012年到2017年城乡居民人民币储蓄存款的变化情况,
并预测该地区2019年的人民币储蓄存款.
附公式: , .
20.(本小题满分12分)
年北京冬奥会的申办成功与“亿人上冰雪”口号的提出,将冰雪这个冷项目迅速炒“热”,北京某综合大学计划在一年级开设冰球课程,为了解学生对冰球运动的兴趣,随机从该校一年级学生中抽取了人进行调查,其中女生中对冰球运动有兴趣的占,而男生有人表示对冰球运动没有兴趣.
(1)完成列联表,并回答能否有的把握认为“对冰球是否有兴趣与性别有关”?
有兴趣
没兴趣
合计
男
女
合计
(2)已知在被调查的女生中有名数学系的学生,其中名对冰球有兴趣,现在从这名学生中随机抽取人,求至少有人对冰球有兴趣的概率.
附:临界值表、公式
0.15
0.10
0.050
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
21.(本小题满分12分)
在直角坐标系中,以坐标原点为极点,轴的正半轴为极轴,建立极坐标系,
直线的参数方程为,圆的极坐标方程为.
(1)求直线的普通方程与圆的直角坐标方程;
(2)设曲线与直线交于两点,若点的直角坐标为,求的值.
22.(本小题满分12分)
如图,椭圆经过点,离心率,直线的方程为.
(1)求椭圆的方程;
(2)设过椭圆右焦点的直线与直线相交于点,记直线的斜率分别为,问:是否存在常数,使得?若存在,求的值;若不存在,请说明理由.
大庆实验中学2018-2019学年度下学期开学考试
高二 数学(文) 参考答案
1
2
3
4
5
6
7
8
9
10
11
12
【解析】
(1)设数列的公差为,由题意得,由得
所以的通项公式为
(2)由(1)得,所以当时,取得最小值,最小值为.
【解析】(1)由
的最小正周期
令,解得
故的单调递增区间
(2),,
,则的值域是.
【解析】
(1),
(2)2012年到2017年储蓄存款逐年增长,每年约增长2019年预测存款为千亿元.
【解析】(1)根据已知数据得到如下列联表
有兴趣
没有兴趣
合计
男
45
10
55
女
30
15
45
合计
75
25
100
由列联表中的数据可得
所以有90%的把握认为“对冰球是否有兴趣与性别有关”.
(2)记5人中对冰球有兴趣的3人为A、B、C,对冰球没有兴趣的2人为x,y,
则从这5人中随机抽取3人的基本事件为:(Axy),(Bxy),(Cxy),(ABx),
(ABy),(BCx),(BCy),(ACx),(ACy),(ABC),共10种情况,
至少2人对冰球有兴趣的基本事件为:(ABC),(ABx),(ABy),(BCx),(BCy)
(ACx),(ACy)共7种, 设至少2人对冰球有兴趣为事件D,
【解析】解析:(1)直线的普通方程为: ,
,所以.
所以曲线的直角坐标方程为(或写成)..
(2)点P(2,1)在直线上,且在圆C内,把代入,得,设两个实根为,则,即异号.
所以.
【解析】
(1)由在椭圆上,得,
又,得,由①②,得,,,故椭圆
的方程为
(2)显然直线斜率一定存在,设直线的方程为
由,∴,,
∴
又将代入得,
∴,∴故存在常数符合题意.