中考数学总复习专题课件：圆与圆的位置关系（二） 8页

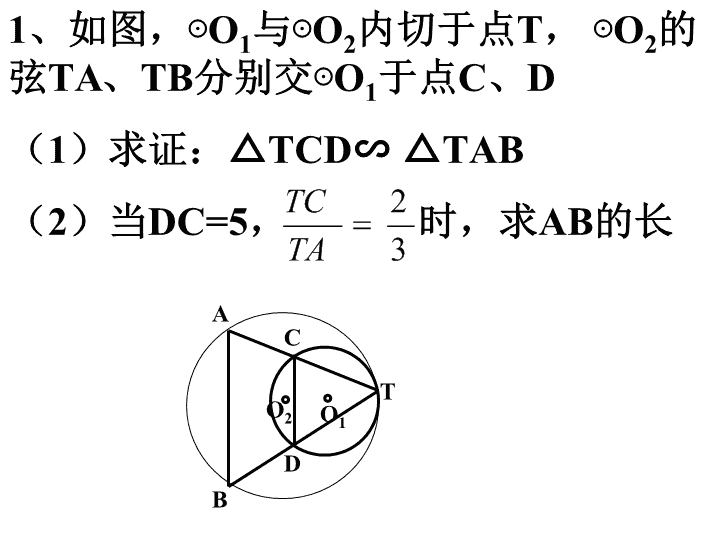
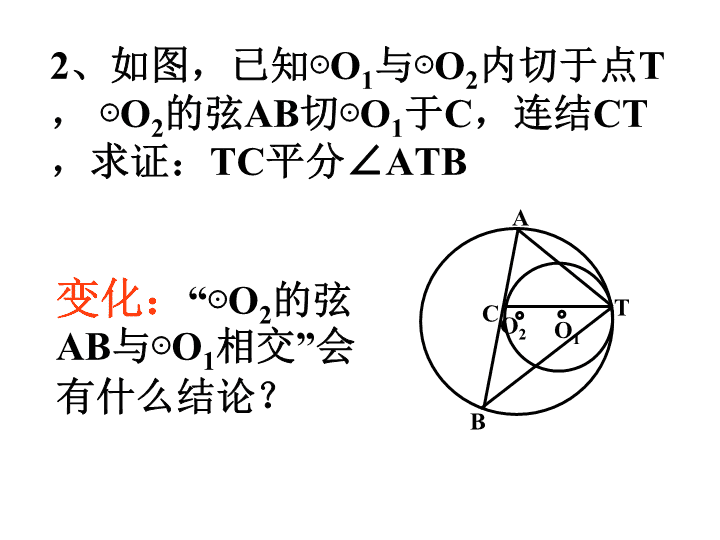
1、如图，⊙ O 1 与⊙ O 2 内切于点 T， ⊙ O 2 的弦 TA、TB 分别交⊙ O 1 于点 C、D （1） 求证：△ TCD∽ △ TAB （2） 当 DC=5， 时，求 AB 的长 O 1 O 2 T A B C D 2、如图，已知⊙ O 1 与⊙ O 2 内切于点 T， ⊙ O 2 的弦 AB 切⊙ O 1 于 C， 连结 CT， 求证： TC 平分∠ ATB C O 1 O 2 T A B 变化： “⊙ O 2 的弦 AB 与⊙ O 1 相交”会有什么结论？ 3、如图， ⊙ O 1 与⊙ O 2 内切于点 A，O 2 在⊙ O 1 上， B 是 O 2 A 上一点， BD⊥OA 交⊙ O 2 于 D， 交⊙ O 1 于 C， 连结 AD 交⊙ O 1 于 E， 则（1） E 是 AD 上一个怎样的点？试证明，（2） AD 与 AC 是怎样的倍数关系？写出关系式，并证明。 O 2 O 1 A D E B C 4、如图，已知⊙ O 1 与⊙ O 2 外切于 M 点， AC 是两圆的外公切线， A、C 为切点，连 AM 并延长交⊙ O 2 于 D （1） 求证： CM 2 =AM·MD D A C M O 1 O 2 4、如图，已知⊙ O 1 与⊙ O 2 外切于 M 点， AC 是两圆的外公切线， A、C 为切点，连 AM 并延长交⊙ O 2 于 D （2） 如图，若移动点 A，AC 保持与相切⊙ O 2 于 C，AC 交⊙ O 1 于 B， 则 CM 2 =______( 请在横线上填写图中的两条线段的乘积）并证明之。 D A C M O 1 O 2 B 4、如图，已知⊙ O 1 与⊙ O 2 外切于 M 点， AC 是两圆的外公切线， A、C 为切点，连 AM 并延长交⊙ O 2 于 D。 （3）如图，将圆的外公切线变为两圆的割线，交点分别为 A、B、C、E， 则 MC·ME=______( 请在横线上填写图中的某两条线段的乘积）并证明之。 D A C M O 1 O 2 B E 变式： 如图， ⊙ O 1 与⊙ O 2 外切于 P，AB 过点 P， 分别交⊙ O 1 和⊙ O 2 于 A、B，BH 切⊙ O 2 于 B， 交⊙ O 1 于 C、H。 （1） 求证：△ BCP∽ △ HAP （2）若 AP：PB=3：2， 且 C 为 HB 的中点，求 AH：BC A C P O 1 O 2 B H