- 400.00 KB
- 2021-05-28 发布
2016-2017学年江西省赣州市崇义中学高二(上)第一次月考数学试卷(理科)
一、选择题(本题共12小题,每小题5分,共60分)
1.如图所示,下列符号表示错误的是( )
A.l∈α B.P∉l C.l⊊α D.P∈α
2.用一个平面去截四棱锥,不可能得到( )
A.棱锥 B.棱柱 C.棱台 D.四面体
3.水平放置的△ABC的直观图如图,其中B′O′=C′O′=1,A′O′=,那么原△ABC是一个( )
A.等边三角形
B.直角三角形
C.三边中只有两边相等的等腰三角形
D.三边互不相等的三角形
4.已知<<0,则下列结论不正确的是( )
A.a2<b2 B.ab<b2 C. +>2 D.|a|+|b|>|a+b|
5.已知正方体的棱长为1,且其顶点都在一个球面上,则该球的表面积为( )
A.π B.2π C.3π D.4π
6.设有直线m、n和平面α、β,下列四个命题中,正确的是( )
A.若m∥α,n∥α,则m∥n B.若m⊂α,n⊂α,m∥β,n∥β,则α∥β
C.若α⊥β,m⊂α,则m⊥β D.若α⊥β,m⊥β,m⊄α,则m∥α
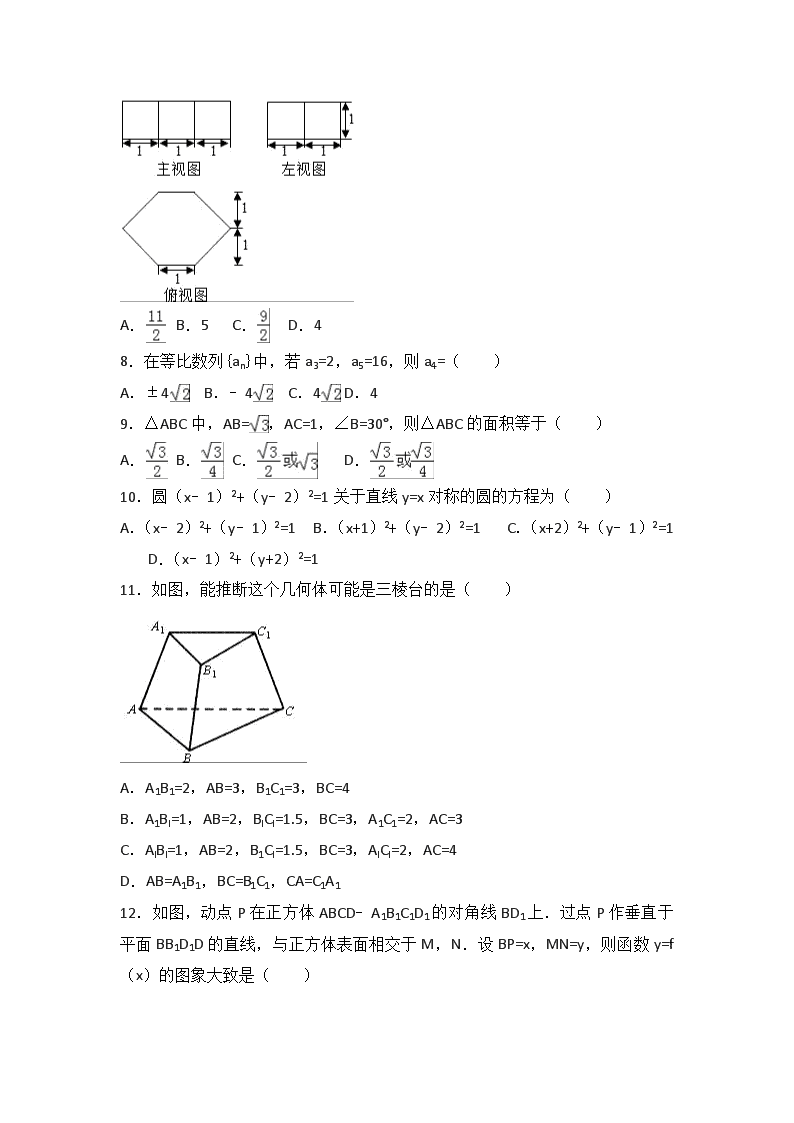
7.若一个几何体的三视图如图所示,则此几何体的体积为( )
A. B.5 C. D.4
8.在等比数列{an}中,若a3=2,a5=16,则a4=( )
A.±4 B.﹣4 C.4 D.4
9.△ABC中,AB=,AC=1,∠B=30°,则△ABC的面积等于( )
A. B. C. D.
10.圆(x﹣1)2+(y﹣2)2=1关于直线y=x对称的圆的方程为( )
A.(x﹣2)2+(y﹣1)2=1 B.(x+1)2+(y﹣2)2=1 C.(x+2)2+(y﹣1)2=1 D.(x﹣1)2+(y+2)2=1
11.如图,能推断这个几何体可能是三棱台的是( )
A.A1B1=2,AB=3,B1C1=3,BC=4
B.A1Bl=1,AB=2,BlCl=1.5,BC=3,A1C1=2,AC=3
C.AlBl=1,AB=2,B1Cl=1.5,BC=3,AlCl=2,AC=4
D.AB=A1B1,BC=B1C1,CA=C1A1
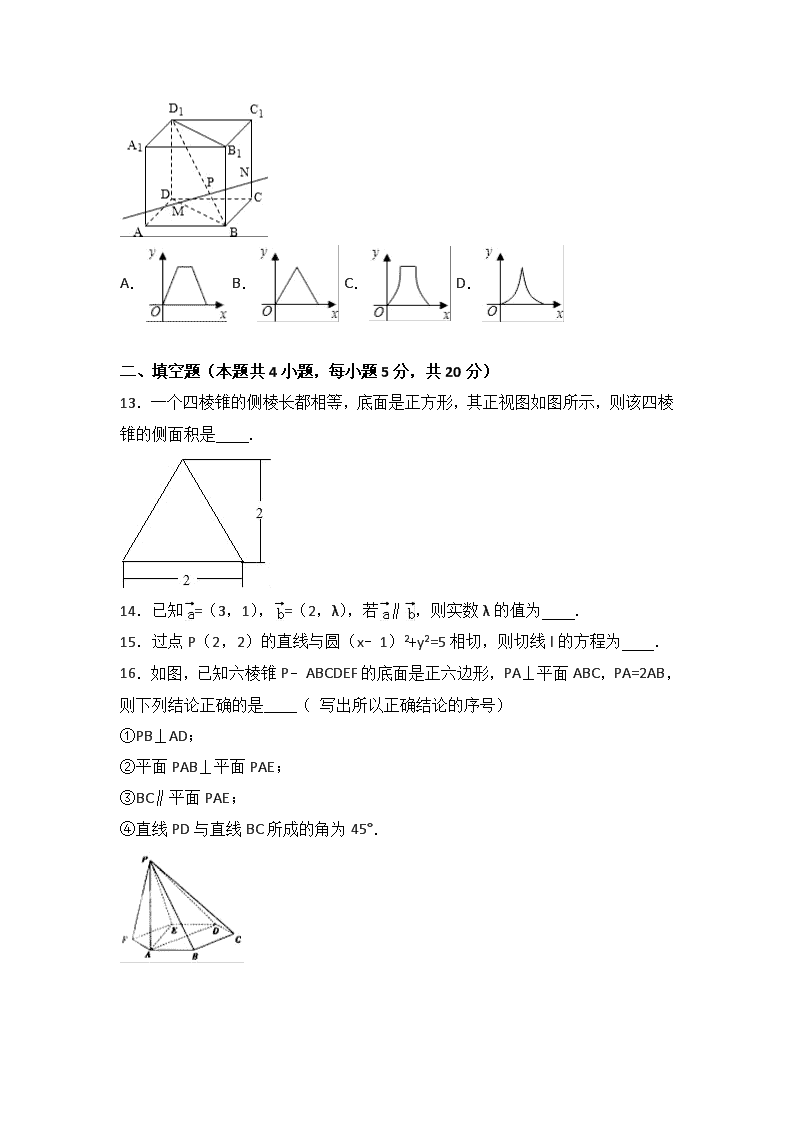
12.如图,动点P在正方体ABCD﹣A1B1C1D1的对角线BD1上.过点P作垂直于平面BB1D1D的直线,与正方体表面相交于M,N.设BP=x,MN=y,则函数y=f(x)的图象大致是( )
A. B. C. D.
二、填空题(本题共4小题,每小题5分,共20分)
13.一个四棱锥的侧棱长都相等,底面是正方形,其正视图如图所示,则该四棱锥的侧面积是 .
14.已知=(3,1),=(2,λ),若∥,则实数λ的值为 .
15.过点P(2,2)的直线与圆(x﹣1)2+y2=5相切,则切线l的方程为 .
16.如图,已知六棱锥P﹣ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是 ( 写出所以正确结论的序号)
①PB⊥AD;
②平面PAB⊥平面PAE;
③BC∥平面PAE;
④直线PD与直线BC所成的角为45°.
三、解答题(本题共6小题,共70分)
17.已知三角形的三个顶点是A(4,0),B(6,6),C(0,2).
(1)求AB边上的高所在直线的方程;
(2)求AC边上的中线所在直线的方程.
18.已知等差数列{an},其中a1+a2+a3=﹣3,a1•a2•a3=8.
(1)求等差数列{an}的通项公式;
(2)若a2,a3,a1成等比数列,则求{an+7}的前n项和.
19.如图,已知一个圆锥的底面半径与高均为2,且在这个圆锥中有一个高为x的圆柱.
(1)用x表示此圆柱的侧面积表达式;
(2)当此圆柱的侧面积最大时,求此圆柱的体积.
20.如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证:
(Ⅰ)PA∥平面BDE;
(Ⅱ)平面PAC⊥平面BDE.
21. 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
(1)求证:AC⊥平面BDE;
(2)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥
平面BEF,并证明你的结论.
22.已知圆M:x2+y2﹣2y=24,直线l:x+y=11,l上一点A的横坐标为a,过点A作圆M的两条切线l1,l2,切点分别为B,C.
(1)当a=0时,求直线l1,l2的方程;
(2)当直线 l1,l2互相垂直时,求a的值;
(3)是否存在点A,使得•=﹣2?若存在,求出点A的坐标,若不存在,请说明理由.
2016-2017学年江西省赣州市崇义中学高二(上)第一次月考数学试卷(理科)
参考答案与试题解析
一、选择题(本题共12小题,每小题5分,共60分)
1.如图所示,下列符号表示错误的是( )
A.l∈α B.P∉l C.l⊊α D.P∈α
【考点】空间中直线与平面之间的位置关系.
【分析】根据空间点,线,平面之间的位置关系进行判断即可.
【解答】解:A.直线l在平面内,用符号表示为l⊊α,∴A错误.
B.点P不在直线l上,用符号表示为P∉l,∴B正确.
C.直线l在平面内,用符号表示为l⊊α,∴C正确.
D.点P在平面内,用符号表示为P∈α,∴D正确.
故选:A.
2.用一个平面去截四棱锥,不可能得到( )
A.棱锥 B.棱柱 C.棱台 D.四面体
【考点】棱锥的结构特征.
【分析】根据棱柱的定义进行判断.
【解答】解:∵棱柱的上下底面是相同的,
∴用一个平面去截四棱锥,不可能得到棱柱.
故选:B.
3.水平放置的△ABC的直观图如图,其中B′O′=C′O′=1,A′O′=,那么原△ABC是一个( )
A.等边三角形
B.直角三角形
C.三边中只有两边相等的等腰三角形
D.三边互不相等的三角形
【考点】平面图形的直观图.
【分析】由图形和A′O′=通过直观图的画法知在原图形中三角形的底边BC=B'C',AO⊥BC,且AO=,故三角形为正三角形.
【解答】解:由图形知,在原△ABC中,AO⊥BC,
∵A′O′=
∴AO=
∵B′O′=C′O′=1∴BC=2
∴AB=AC=2
∴△ABC为正三角形.
故选A
4.已知<<0,则下列结论不正确的是( )
A.a2<b2 B.ab<b2 C. +>2 D.|a|+|b|>|a+b|
【考点】不等式的基本性质.
【分析】由于<<0,可得b<a<0,因此b2>a2,ab<b2, =2,|a|+|b|=|a+b|,即可判断出.
【解答】解:∵<<0,
∴b<a<0,
∴b2>a2,ab<b2, =2,|a|+|b|=|a+b|,
因此只有D不正确.
故选:D.
5.已知正方体的棱长为1,且其顶点都在一个球面上,则该球的表面积为( )
A.π B.2π C.3π D.4π
【考点】球的体积和表面积.
【分析】设出正方体的棱长,求出正方体的体对角线的长,就是球的直径,求出球的表面积即可.
【解答】解:设正方体的棱长为:1,正方体的体对角线的长为:,就是球的直径,
∴球的表面积为:S2=4π()2=3π.
故选:C.
6.设有直线m、n和平面α、β,下列四个命题中,正确的是( )
A.若m∥α,n∥α,则m∥n B.若m⊂α,n⊂α,m∥β,n∥β,则α∥β
C.若α⊥β,m⊂α,则m⊥β D.若α⊥β,m⊥β,m⊄α,则m∥α
【考点】空间中直线与平面之间的位置关系.
【分析】由面面平行的判定定理和线面平行的定理判断A、B、D;由面面垂直的性质定理判断C.
【解答】解:A不对,由面面平行的判定定理知,m与n可能相交,也可能是异面直线;B不对,由面面平行的判定定理知少相交条件;
C不对,由面面垂直的性质定理知,m必须垂直交线;
故选:D.
7.若一个几何体的三视图如图所示,则此几何体的体积为( )
A. B.5 C. D.4
【考点】由三视图求面积、体积.
【分析】先根据三视图判断此几何体为直六棱柱,再分别计算棱柱的底面积和高,最后由棱柱的体积计算公式求得结果
【解答】解:由图可知,此几何体为直六棱柱,底面六边形可看做两个全等的等腰梯形,上底边为1,下底边为3,高为1,
∴棱柱的底面积为2×=4,
棱柱的高为1
∴此几何体的体积为V=4×1=4
故选D
8.在等比数列{an}中,若a3=2,a5=16,则a4=( )
A.±4 B.﹣4 C.4 D.4
【考点】等比数列的通项公式.
【分析】由题意可得a42=a3•a5,代值计算可得.
【解答】解:由等比数列的性质可得a42=a3•a5,
∴a42=2×16=32,
∴a4=±4
故选:A.
9.△ABC中,AB=,AC=1,∠B=30°,则△ABC的面积等于( )
A. B. C. D.
【考点】解三角形.
【分析】由AB,AC及cosB的值,利用余弦定理即可列出关于BC的方程,求出方程的解即可得到BC的长,然后利用三角形的面积公式,由AB,BC以及sinB的值即可求出△ABC的面积.
【解答】解:由AB=,AC=1,cosB=cos30°=,
根据余弦定理得:AC2=AB2+BC2﹣2AB•BCcosB,即1=3+BC2﹣3BC,
即(BC﹣1)(BC﹣2)=0,解得:BC=1或BC=2,
当BC=1时,△ABC的面积S=AB•BCsinB=××1×=;
当BC=2时,△ABC的面积S=AB•BCsinB=××2×=,
所以△ABC的面积等于或.
故选D
10.圆(x﹣1)2+(y﹣2)2=1关于直线y=x对称的圆的方程为( )
A.(x﹣2)2+(y﹣1)2=1 B.(x+1)2+(y﹣2)2=1 C.(x+2)2+(y﹣1)2=1 D.(x﹣1)2+(y+2)2=1
【考点】圆的标准方程.
【分析】根据平面直角坐标系内点P关于直线y=x对称的点对称点P'的坐标公式,可得圆心坐标,即可得出圆的方程.
【解答】解:∵点P(x,y)关于直线y=x对称的点为P'(y,x),
∴(1,2)关于直线y=x对称的点为(2,1),
∴圆(x﹣1)2+(y﹣2)2=1关于直线y=x对称的圆的方程为(x﹣2)2+(y﹣1)2=1.
故选:A.
11.如图,能推断这个几何体可能是三棱台的是( )
A.A1B1=2,AB=3,B1C1=3,BC=4
B.A1Bl=1,AB=2,BlCl=1.5,BC=3,A1C1=2,AC=3
C.AlBl=1,AB=2,B1Cl=1.5,BC=3,AlCl=2,AC=4
D.AB=A1B1,BC=B1C1,CA=C1A1
【考点】棱台的结构特征.
【分析】推断满足下面四个条件的几何体能否成为三棱台,从两个底面上对应边的比值是否相等,比值相等是组成棱台的必要条件,但这个条件不成立,一定不是棱台.
【解答】解:根据棱台是由棱锥截成的,
A、,故A不正确;
B、,故B不正确;
C、,故C正确,
D、满足这个条件的是一个三棱柱,不是三棱台,
故选C.
12.如图,动点P在正方体ABCD﹣A1B1C1D1的对角线BD1上.过点P作垂直于平面BB1D1D的直线,与正方体表面相交于M,N.设BP=x,MN=y,则函数y=f(x)的图象大致是( )
A. B. C. D.
【考点】空间中直线与直线之间的位置关系.
【分析】只有当P移动到正方体中心O时,MN有唯一的最大值,则淘汰选项A、C;P点移动时,x与y的关系应该是线性的,则淘汰选项D.
【解答】解:设正方体的棱长为1,显然,当P移动到对角线BD1的中点O时,函数取得唯一最大值,所以排除A、C;
当P在BO上时,分别过M、N、P作底面的垂线,垂足分别为M1、N1、P1,
则y=MN=M1N1=2BP1=2•xcos∠D1BD=2•是一次函数,所以排除D.
故选B.
二、填空题(本题共4小题,每小题5分,共20分)
13.一个四棱锥的侧棱长都相等,底面是正方形,其正视图如图所示,则该四棱锥的侧面积是 4 .
【考点】简单空间图形的三视图.
【分析】由题意可知原四棱锥为正四棱锥,由四棱锥的主视图得到四棱锥的底面边长和高,则其侧面积和体积可求
【解答】解:因为四棱锥的侧棱长都相等,底面是正方形,所以该四棱锥为正四棱锥,
其主视图为原图形中的三角形PEF,如图,
由该四棱锥的主视图可知四棱锥的底面边长AB=2,
高PO=2,
则四棱锥的斜高PE==.
所以该四棱锥侧面积S=4××2×=4,
故答案是4.
14.已知=(3,1),=(2,λ),若∥,则实数λ的值为 .
【考点】平行向量与共线向量.
【分析】根据平面向量的共线定理,列出方程解方程即可.
【解答】解: =(3,1),=(2,λ),
若∥,则3λ﹣2×1=0,
解得λ=.
故答案为:.
15.过点P(2,2)的直线与圆(x﹣1)2+y2=5相切,则切线l的方程为 x+2y﹣6=0 .
【考点】圆的切线方程.
【分析】设出切线方程,求出圆的圆心与半径,利用圆心到直线的距离等于半径,求出k,写出切线方程即可.
【解答】解:设切线方程为y﹣2=k(x﹣2),即kx﹣y﹣2k+2=0,
∵圆心(1,0)到切线l的距离等于半径,
∴=,解得k=﹣,
∴切线方程为y﹣2=﹣(x﹣2),即x+2y﹣6=0,
故答案为x+2y﹣6=0.
16.如图,已知六棱锥P﹣ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是 ④ ( 写出所以正确结论的序号)
①PB⊥AD;
②平面PAB⊥平面PAE;
③BC∥平面PAE;
④直线PD与直线BC所成的角为45°.
【考点】异面直线及其所成的角;直线与平面平行的判定;平面与平面垂直的判定.
【分析】在①中,AD与PB在平面的射影AB不垂直;在②中,平面PAB⊥平面PAE;在③中,BC∥平面PAD;在④中,在Rt△PAD中,PA=AD=2AB,从而∠PDA=45°.
【解答】解:在①中,∵AD与PB在平面的射影AB不垂直,∴①不成立;
在②中,∵平面PAB⊥平面PAE,∴平面PAB⊥平面PBC也不成立,即②不成立;
在③中,∵BC∥AD,BC⊄平面PAD,AD⊂平面PAD,∴BC∥平面PAD,
∴直线BC∥平面PAE也不成立,故③不成立;
在④中,在Rt△PAD中,PA=AD=2AB,∴∠PDA=45°,故④正确.
故答案为:④.
三、解答题(本题共6小题,共70分)
17.已知三角形的三个顶点是A(4,0),B(6,6),C(0,2).
(1)求AB边上的高所在直线的方程;
(2)求AC边上的中线所在直线的方程.
【考点】直线的一般式方程与直线的垂直关系.
【分析】(1)由=3,知AB边上的高所在直线的斜率k=﹣,由此利用点斜式方程级求出AB边上的高所在直线的方程.
(2)由AC边的中点为(2,1),利用两点式方程级求出AC边上的中线所在直线的方程.
【解答】解:(1)∵A(4,0),B(6,6),C(0,2),
∴=3,∴AB边上的高所在直线的斜率k=﹣,
∴AB边上的高所在直线的方程为y﹣2=﹣,
整理,得x+3y﹣6=0.
(2)∵AC边的中点为(2,1),
∴AC边上的中线所在的直线方程为,
整理,得5x﹣4y﹣6=0.
18.已知等差数列{an},其中a1+a2+a3=﹣3,a1•a2•a3=8.
(1)求等差数列{an}的通项公式;
(2)若a2,a3,a1成等比数列,则求{an+7}的前n项和.
【考点】数列的求和.
【分析】(1)设等差数列{an}的公差为d,运用等差数列的通项公式和性质,求得首项和公差,即可得到所求通项公式;
(2)运用等比数列中项性质可得a3=2,a1=﹣4,a2=﹣1,进而得到an+7=3n,运用等差数列的求和公式即可得到所求和.
【解答】解:(1)设等差数列{an}的公差为d,
由a1+a2+a3=﹣3,a1•a2•a3=8.
可得3a1+3d=﹣3,即a2=﹣1,
a1+a3=﹣2,a1•a3=﹣8.
解得a1=﹣4,a3=2或a1=2,a3=﹣4,
则d=3或﹣3,
则an=﹣4+3(n﹣1)=3n﹣7;或an=2﹣3(n﹣1)=5﹣3n;
(2)a2,a3,a1成等比数列,
可得a32=a1a2,
又a1•a2•a3=8,可得a3=2,a1=﹣4,a2=﹣1,
则an+7=3n,
可得{an+7}的前n项和为n(3+3n)=(n2+n).
19.如图,已知一个圆锥的底面半径与高均为2,且在这个圆锥中有一个高为x的圆柱.
(1)用x表示此圆柱的侧面积表达式;
(2)当此圆柱的侧面积最大时,求此圆柱的体积.
【考点】旋转体(圆柱、圆锥、圆台).
【分析】(1)设圆柱的底面半径为r,根据相似比求出r与x的关系,代入侧面积公式即可;
(2)利用二次函数的性质求出侧面积最大时x的值,代入体积公式即可.
【解答】解:(1)设圆柱的半径为r,则,∴r=2﹣x,0<x<2.
∴S圆柱侧=2πrx=2π(2﹣x)x=﹣2πx2+4πx.(0<x<2).
(2),
∴当x=1时,S圆柱侧取最大值2π,
此时,r=1,所以.
20.如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证:
(Ⅰ)PA∥平面BDE;
(Ⅱ)平面PAC⊥平面BDE.
【考点】平面与平面垂直的判定;直线与平面平行的判定.
【分析】(I)根据线面平行的判定定理证出即可;(II)根据面面垂直的判定定理证明即可.
【解答】证明:(I)∵O是AC的中点,E是PC的中点,
∴OE∥AP,又∵OE⊂平面BDE,PA
⊄平面BDE.
∴PA∥平面BDE.
(II)∵PO⊥底面ABCD,PO⊥BD,
又∵AC⊥BD,且AC∩PO=O
∴BD⊥平面PAC,而BD⊂平面BDE,
∴平面PAC⊥平面BDE
21. 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
(1)求证:AC⊥平面BDE;
(2)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
【考点】直线与平面垂直的判定;直线与平面平行的判定.
【分析】(1)根据DE⊥平面ABCD,由线面垂直的判定定理可知DE⊥AC,由ABCD是正方形可知AC⊥BD,而DE∩BD=D,满足线面垂直的判定所需条件,从而证得结论;
(2)当M是BD的一个三等分点,即3BM=BD时,AM∥平面BEF.取BE上的三等分点N,使3BN=BE,连接MN,NF,则DE∥MN,且DE=3MN,而AF∥DE,且DE=3AF,则四边形AMNF是平行四边形,从而AM∥FN,AM⊄平面BEF,FN⊂平面BEF,满足线面平行的判定定理,从而证得结论.
【解答】(1)证明:因为DE⊥平面ABCD,
所以DE⊥AC.…
因为ABCD是正方形,
所以AC⊥BD,因为DE∩BD=D…
从而AC⊥平面BDE.…
(2)当M是BD的一个三等分点,即3BM=BD时,AM∥平面BEF. …
取BE上的三等分点N,使3BN=BE,连接MN,NF,则DE∥MN,且DE=3MN,
因为AF∥DE,且DE=3AF,所以AF∥MN,且AF=MN,
故四边形AMNF是平行四边形. …
所以AM∥FN,
因为AM⊄平面BEF,FN⊂平面BEF,…
所以AM∥平面BEF. …
22.已知圆M:x2+y2﹣2y=24,直线l:x+y=11,l上一点A的横坐标为a,过点A作圆M的两条切线l1,l2,切点分别为B,C.
(1)当a=0时,求直线l1,l2的方程;
(2)当直线 l1,l2互相垂直时,求a的值;
(3)是否存在点A,使得•=﹣2?若存在,求出点A的坐标,若不存在,请说明理由.
【考点】直线和圆的方程的应用.
【分析】(1)利用圆心到直线的距离等于半径,求出直线的斜率,即可求直线l1,l2的方程;
(2)当直线 l1,l2互相垂直时,四边形MCAB为正方形,即可求a的值;
(3)设,可得,利用圆心M到直线l的距离是,即可得出结论.
【解答】解:(1))圆M:x2+(y﹣1)2=25,圆心M(0,1),半径r=5,A(0,11),设切线的方程为y=kx+11,圆心距,
∴,
∴所求直线l1,l2的方程为;
(2)当l1⊥l2时,四边形MCAB为正方形,
∴
设A(a,11﹣a),M(0,1),则,
∴a2﹣10a+25=0,∴a=5;
(3)设,则
,
又,故,
又圆心M到直线l的距离是,
∴AM2≥50,
∴,故点A不存在.
2017年4月19日