- 903.50 KB
- 2021-05-28 发布
第二十二章 二次函数
22.3 实际问题与二次函数
第1课时 几何图形的最大面积
写出下列抛物线的开口方向、对称轴和顶点坐标,并写出其最值.
(1)y=x2-4x-5; (配方法) (2)y=-x2-3x+4.(公式法)
解:(1)开口方向:向上;对称轴:x=2;顶点坐标:
(2,-9);最小值:-9;
(2)开口方向:向下;对称轴:x= ;顶点坐标:
( , );最大值: .
3- 23- 2
25
4
25
4
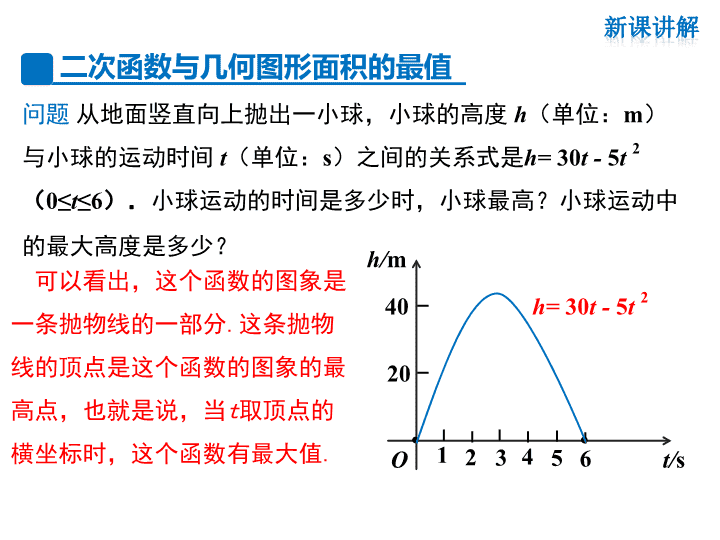
问题 从地面竖直向上抛出一小球,小球的高度 h(单位:m)
与小球的运动时间 t(单位:s)之间的关系式是h= 30t - 5t 2
(0≤t≤6).小球运动的时间是多少时,小球最高?小球运动中
的最大高度是多少?
t/s
h/m
O 1 2 3 4 5 6
20
40 h= 30t - 5t 2
可以看出,这个函数的图象是
一条抛物线的一部分.这条抛物
线的顶点是这个函数的图象的最
高点,也就是说,当t取顶点的
横坐标时,这个函数有最大值.
二次函数与几何图形面积的最值
由于抛物线 y = ax 2 + bx + c 的顶点是最低(高)点,
当 时,二次函数 y = ax 2 + bx + c 有最小(大)值
2
bx a
24
4
ac by a
.
如何求出二次函数 y = ax 2 + bx + c 的最小(大)值?
小球运动的时间是 3s 时,小球最高.小
球运动中的最大高度是 45 m.
30 32 2 5
bt a
( ) ,
2 24 30 454 4 5
ac bh a
( ) .
t/s
h/m
O 1 2 3 4 5 6
20
40 h= 30t - 5t 2
问题1 矩形面积公式是什么?
问题2 如何用l表示另一边?
问题3 面积S的函数关系式是什么?
用总长为60m的篱笆围成矩形场地,矩形面积S随矩形
一边长l的变化而变化.当l是多少米时,场地的面积S最大?
例题
解:矩形场地的周长是60m,一边
唱为lm,所以另一边长为( -
l )m.场地的面积
S=l(30-l),
即 S=-l2+30l (0
相关文档
- 人教部编版小学二年级语文下册课堂2021-05-28 16:32:4518页
- 统编版二年级语文上册-(课堂教学课2021-05-28 15:35:0717页
- 最新部编版八年级上册道德与法治课2021-05-28 15:02:18442页
- 统编版二年级语文上册-(课堂教学课2021-05-28 14:49:4513页
- 人教部编版九年级下册语文课堂教学2021-05-28 14:41:5812页
- 部编版 小学一年级下册语文(课堂教2021-05-28 14:31:1915页
- 人教部编版小学二年级语文下册课堂2021-05-28 14:19:0226页
- 部编版 小学一年级下册语文(课堂教2021-05-28 14:15:3023页
- 部编版 小学一年级下册语文(课堂教2021-05-28 14:12:4831页
- 部编版 小学一年级下册语文(课堂教2021-05-28 13:57:549页