北师大版数学九年级上册同步练习课件-期末复习2一元二次方程 26页

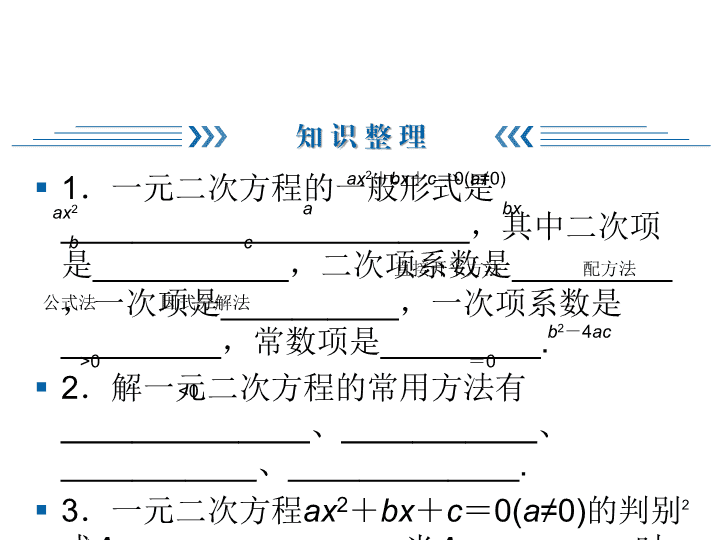
期末复习 期末复习2　一元二次方程 § 1．一元二次方程的一般形式是 _______________________，其中二次项 是___________，二次项系数是_________， 一次项是__________，一次项系数是 _________，常数项是_________. § 2．解一元二次方程的常用方法有 ______________、___________、 ___________、_____________. § 3．一元二次方程ax2＋bx＋c＝0(a≠0)的判别 式Δ＝______________.当Δ__________时， 方程有两个不相等的实数根；当 Δ__________时，方程有两个相等的实数根； 当Δ__________时，方程没有实数根． 2 ax2＋bx＋c＝0(a≠0)　 ax2 a bx b c 直接开平方法 配方法 公式法 因式分解法 b2－4ac　 >0　 ＝0 <0 § 4．一元二次方程ax2＋bx＋c＝0(a≠0)的求根公式是___________________. § 5．若x1、x2是方程ax2＋bx＋c＝0(a≠0)的两根，则x1＋x2＝__________，x1x2＝_________. § 6．利用一元二次方程解决实际问题时，求得的结果一定要使 _______________. 3 实际问题有意义 § ★集训1　一元二次方程的解法 § 1．解方程：(x－5)2＝16. § 解：方程两边开平方，得x－5＝±4.所以x1 ＝1，x2＝9. § 2．用配方法解方程：x2－4x＋1＝0. 4 § 3．解方程：2x(x＋4)＝1. § 4．用适当的方法解方程：4x－6＝(3－2x)x. 5 § ★集训2　一元二次方程的根与系数的关系的 运用 § 5．【山东烟台中考】若x1、x2是方程x2－ 2mx＋m2－m－1＝0的两个根，且x1＋x2＝1 －x1x2，则m的值为(　　) § A．－1或2 B．1或－2 § C．－2 D．1 6 D 　 47 　 § 7．【湖北十堰中考】已知关于x的方程x2＋ (2k－1)x＋k2－1＝0有两个实数根x1、x2. § (1)求实数k的取值范围； § (2)若x1、x2满足x＋x＝16＋x1x2，求实数k的 值． 7 8 9 10 § ★集训3　一元二次方程的实际应用 § 9．今年“十一”长假某湿地公园迎来旅游高 峰，第一天的游客人数是1.2万人，第三天的 游客人数为2.3万人．假设每天游客增加的百 分率相同且设为x，则根据题意可列方程为(　 　) § A．2.3(1＋x)2＝1.2 § B．1.2(1＋x)2＝2.3 § C．1.2(1－x)2＝2.3 § D．1.2＋1.2(1＋x)＋1.2(1＋x)2＝2.3 § 10．一次会议上，每两个参加会议的人都互 相握手一次，有人统计一共握手66次，则这 次会议到会人数是__________人． 11 B 　 12　 § 11．某商店从厂家以每件18元购进一批商品 出售，若每件售价为a元，则可售出(320－ 10a)件，但物价部门限定每件商品加价不能 超过进价的25%，若商店要想获得400元利 润，则售价应定为每件多少元？需售出这种 商品多少件？ § 解：设每件商品的售价定为a元．根据题意， 得(a－18)(320－10a)＝400.整理，得a2－ 50a＋616＝0.解得a1＝22，a2＝28.∵18×(1 ＋25%)＝22.5，而28＞22.5，∴a＝22，卖 出商品的件数为320－10×22＝100.即每件 商品的售价应定为22元，需要卖出这种商品 100件． 12 § 12．李明准备进行如下操作实验，把一根长40 cm的铁丝剪成两 段，并把每段首尾相连各围成一个正方形． § (1)要使这两个正方形的面积之和等于58 cm2，李明应该怎么剪这 根铁丝？ § (2)李明认为这两个正方形的面积之和不可能等于48 cm2，你认为 他的说法正确吗？请说明理由． 13 14 § 一、选择题(每小题4分，共32分) § 1．某市2015年平均房价为每平方米8000元，2017年平均房价降 到每平方米7000元．设这两年平均房价年平均降低率为x，根据 题意，下面所列方程正确的是 § (　　) § A．8000(1＋x)2＝7000 B．8000(1－x)2＝7000 § C．7000(1－x)2＝8000 D．7000(1＋x)2＝8000 § 2．若关于x的一元二次方程kx2＋2x－1＝0有实数根，则实数k的 取值范围是 § (　　) § A．k≥－1 B．k＞－1 § C．k≥－1且k≠0 D．k＞－1且k≠0 15 B 　 C 　 16 A 　 D 　 17 B 　 C 　 § 7．某商品的进价为每件20元．当售价为每 件30元时，每天可卖出100件，现需降价处 理，且经市场调查：每降价1元，每天可多卖 出10件．现在要使每天利润为750元，每件 商品应降价(　　) § A．2元 B．2.5元 § C．3元 D．5元 18 D 　 19 B 　 20 x2－12x＋14＝0　 －12　 x1＝3，x2＝－1　 －3　 －1或－3　 § 三、解答题(共48分) § 13．(9分)解下列方程： § (1)x2＋4x－5＝0；(2)x(x－4)＝2－8x；(3)x －3＝4(x－3)2. 21 22 § (1)嘉淇的解法从第_________步开始出现错 误； § 事实上，当b2－4ac>0时， § 方程ax2＋bx＋c＝0(a≠0)的求根公式是 ________________________； § (2)用配方法解方程：x2－2x－24＝0. § 解：将x2－2x＝24配方，得x2－2x＋1＝24 ＋1，即(x－1)2＝25.开方，得x－1＝±5.解 得x1＝6，x2＝－4. 23 四　 § 15．(9分)新年到了，班上数学兴趣小组的同 学互赠新年贺卡，每两个同学都相互赠送一 张，小明统计出全组共送了210张贺年卡， 那么数学兴趣小组的人数是多少？ § 解：设数学兴趣小组的人数为x.根据题意， 得x(x－1)＝210，解得x＝15或x＝－14(不合 题意，应舍去)．故数学兴趣小组的人数为15. 24 § 16．(11分)关于x的一元二次方程x2＋(2k＋ 1)x＋k2＋1＝0有两个不相等的实根x1、x2. § (1)求实数k的取值范围； § (2)若方程两实根x1、x2满足x1＋x2＝－x1x2， 求k的值． 25 § 17．(11分)某商场以每件280元的价格购进一 批商品，当每件商品售价为360元时，每月 可售出60件，为了扩大销售，商场决定采取 适当降价的方式促销，经调查发现，如果每 件商品降价1元，那么商场每月就可以多售出 5件． § (1)降价前商场每月销售该商品的利润是多少 元？ § (2)要使商场每月销售这种商品的利润达到 7200元，且更有利于减少库存，则每件商品 应降价多少元？ § 解：(1)由题意，得60×(360－280)＝ 4800(元)．即降价前商场每月销售该商品的 利润是4800元． § (2)设每件商品应降价x元．根据题意，得 (360－x－280)(5x＋60)＝7200.解得 x1＝8， x2＝60.要更有利于减少库存，则x＝60.即要 使商场每月销售这种商品的利润达到7200元， 且更有利于减少库存，则每件商品应降价60 元． 26