高一数学必修5课件-1余弦定理（二） 16页

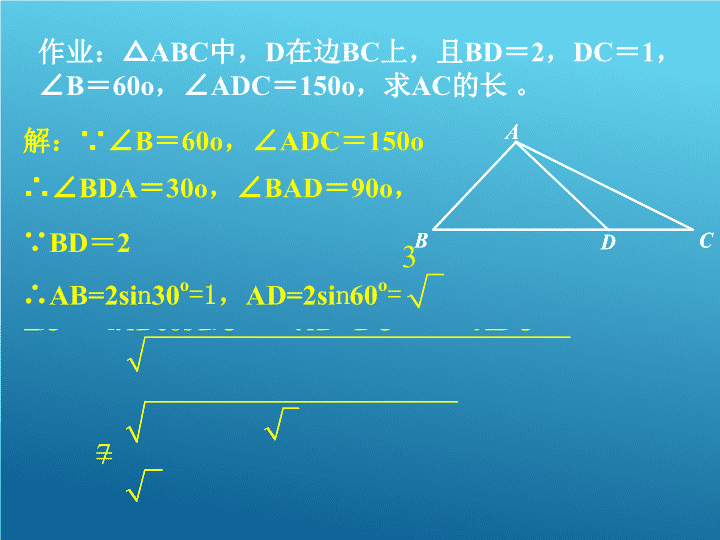
A B CD A B CD 作业：△ABC中，D在边BC上，且BD＝2，DC＝1， ∠B＝60o，∠ADC＝150o，求AC的长 。 解：∵∠B＝60o，∠ADC＝150o ∴∠BDA＝30o，∠BAD＝90o， ∵BD＝2 ∴AB=2sin30o=1，AD=2sin60o= 3 2 2 2 cosAC AD DC AD DC ADC       3 1 2 3 1 cos150       7 一、复习回顾 1、余弦定理： 2a  2 2 2 cosb c bc A  2b  2 2 2 cosa c ac B  2c  2 2 2 cosa b ab C  2、余弦定理的推论： 2 2 2 2 2 2 2 2 2 2 2 2 cos ,cos , cos . b c a a c bA Bbc ac a b cC ab        2 2 3 2 0 2cos( ) 1 ABC A B C a b c a b x x A B c       拓展：已知在 中，角 、 、 所对边长分 别为 、 、 ，其中 、 是方程 的两个根，并且 ，试求 的值。 2 2 21 ABC a b bc c A    在 中例 ， ，则、 若 0120 二、例题分析 2 2 3 2 0a b x x  解： 、 是方程 的两个根 2 3, 2a b ab    ∵2cos(A+B)=1， 1cos 2C   2 2 2 2 22 cosc a b ab C a b ab       10c  2 2( ) (2 3) 2 10a b ab      2 2 3 2 0 2cos( ) 1 ABC A B C a b c a b x x A B c       已知在 中，角 、 、 所对边长分 别为 、 、 ，其中 、 是方 拓展： 程 的两个根，并且 ，试求 的值。 0 0 0 0 5 7 8 ( ) 90 120 135 150A B C D 边长为 ，，的三角形的最大角与最小角 的和是 、 、 、 、 变式、 sin :sin :sin 7 : 8 :132 ABC A B C C    在 中，若 ， 则 例 、 B 120 二、例题分析 0 0 0 0 5 7 8 ( ) 90 120 135 150A B C D 边长为 ，，的三角形的最大角与最小角 的和是 、 、 、 、 例2、 B 二、例题分析 变式、已知a=7、b=8、c=3，则此三角形的形状是（ ） A、钝角三角形 B、直角三角形 C、锐角三角形 D、无法确定 A 0 0 0 0 5 7 8 ( ) 90 120 135 150A B C D 边长为 ，，的三角形的最大角与最小角 的和是 、 、 、 、 例2、 B 二、例题分析 判断三角形是锐角、直角或钝角三角形的方法： 判断最大角的余弦值的符号！ 推广：在△ABC中 （1）若A为直角，则a² ____ b²+c² （2）若A为钝角，则a² ____ b²+c² （3）若A为锐角，则a² ____ b²+c² = > < 解：依题意可得 2 2 1 5 4 9 0 4 9 0 x x x           则 5 13x 解得 ( 5 13)x 的取值范围是 ， 变式：若该三角形是钝角三角形呢？ (1, 5,) ( 13,5) 拓展：若一锐角三角形三条边的长度分别为2、3、x， 试求x的取值范围. 例3、在△ABC中，已知a=bcosC，试判断△ABC的形状。 a=2RsinA b=2RsinB c=2RsinC “边化角” 2 2 2 2 2 2 2 2 2 cos 2 cos 2 cos 2 b c aA bc a c bB ac a b cC ab       “角化边” 在三角形问题中的“边角互化”思想： 二、例题分析 “角化边” sin 2 sin 2 sin 2 aA R bB R cC R    解：(1)由正弦定理可得 cos sin cos 2 2sin sin B b B C a c A C      2sin cos sin cos cos sin 0A B C B C B  即 2sin cos sin( ) 0A B B C    sin( ) sin( ) sinB C A A    2 4 2 1 13 4 cos cos ( ) ( ) ABC a b c A B C B b C a c B b a c a        在 中， 、 、 分别是角 、 、 的对边， 且 求角 的大小； 若 ， 例 ，求 、 的值。 2sin cos sin 0A B A   sin 0 1cos 1202 ABC A B B       在△ 中， ，即 2 4 2 1 13 4 cos cos ( ) ( ) ABC a b c A B C B b C a c B b a c a        在 中， 、 、 分别是角 、 、 的对边， 且 求角 的大小； 若 ， 例 ，求 、 的值。 4 4a c c a   (2) ，故 13, 120b B  又 2 2 2 213 2 cos120a c ac a c ac       2 2( 4) (4 )a a a a     解得 a=1或a=3 2 4 2 1 13 4 cos cos ( ) ( ) ABC a b c A B C B b C a c B b a c a        在 中， 、 、 分别是角 、 、 的对边， 且 求角 的大小； 若 ， 例 ，求 、 的值。 2 4 3 0a a  整理得 02 2 452 2 sinsin sinsin a AB B Bc C     ， ，即 ， 2lg lg lgsin lgABC a c B B     练习 在 中，如果 ， 且 为锐角，试判断此三角 、 形的形状。 2lg lg lgsin lga c B   分析：由 ，得 sin( ) sin sin cos sinB C B C B C    cos sin sin cos cos sinB C B C B C   cos sin sin cos cos sinB C B C B C   cos sin sin cos cos sinB C B C B C   0sin cosB C  。 0cosC  。 090C ABC  即 ，故 为等腰直角三角形。 分析：设△ABC的三个角所对边长分别是a、b、c， 且A≥B≥C， （1）若△ABC是锐角或直角三角形 ∵正弦函数y=sinx在 上是增函数 ∴ 故由正弦定理可得a≥b≥c （2）若△ABC是钝角三角形，则∠A为钝角 ∴π -A< ，且π -A=B+C>B≥C ∴ 即 ∴由正弦定理可得a>b≥c 思考：你能用正弦定理来解释为什么在三角形中越大 的角所对的边就越大吗？ sin sin sinA B C  0 2[ , ] 2  sin( ) sin sinA B C    sin sin sinA B C  3 1 2( ) ABC a b c  在钝角 中， ， ，则最大边 的 取值范围 2 2 2 2 3 5 2 6 3 6 6 3 3 ( ) ( )tan ( ) ABC A B C a b c a c b B ac B A B C D          在 中，角 、 、 的对边分别为 、 、 ， 若 ，则角 的值为 、 、 、 或 、 或 (1)在△ABC中，a2>b2+c2，则角A是（ ） A、钝角 B、直角 C、锐角 D、无法确定 A 5 3c  D 三、针对性练习