- 1.25 MB
- 2024-04-29 发布
绝密★启用前
定远民族中学2017-2018学年度上学期期末考试卷
高二(文科)数学
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、选择题
1.一个棱长都为a的直三棱柱的六个顶点全部在同一个球面上,则该球的表面积为( )
A. B.
C. D.
2.给岀四个命题:
(1)若一个角的两边分别平行于另一个角的两边,则这两个角相等;
(2)为两个不同平面,直线,直线,且,,则a∥b;
(3为两个不同平面,直线,,则;
(4)为两个不同平面,直线,,则.
其中正确的是( )
A.(1)B.(2)C.(3)D.(4)
3.α、β表示平面,a、b表示直线,则a∥α的一个充分条件是( )
A.α⊥β,且a⊥β
B.α∩β=b,且a∥b
C.a∥b,且b∥α
D.α∥β,且a⊂β
4.如图,在直三棱柱中, ,过的中点作平面的垂线,交平面于,则点到平面的距离为( )
A. B. C. D.
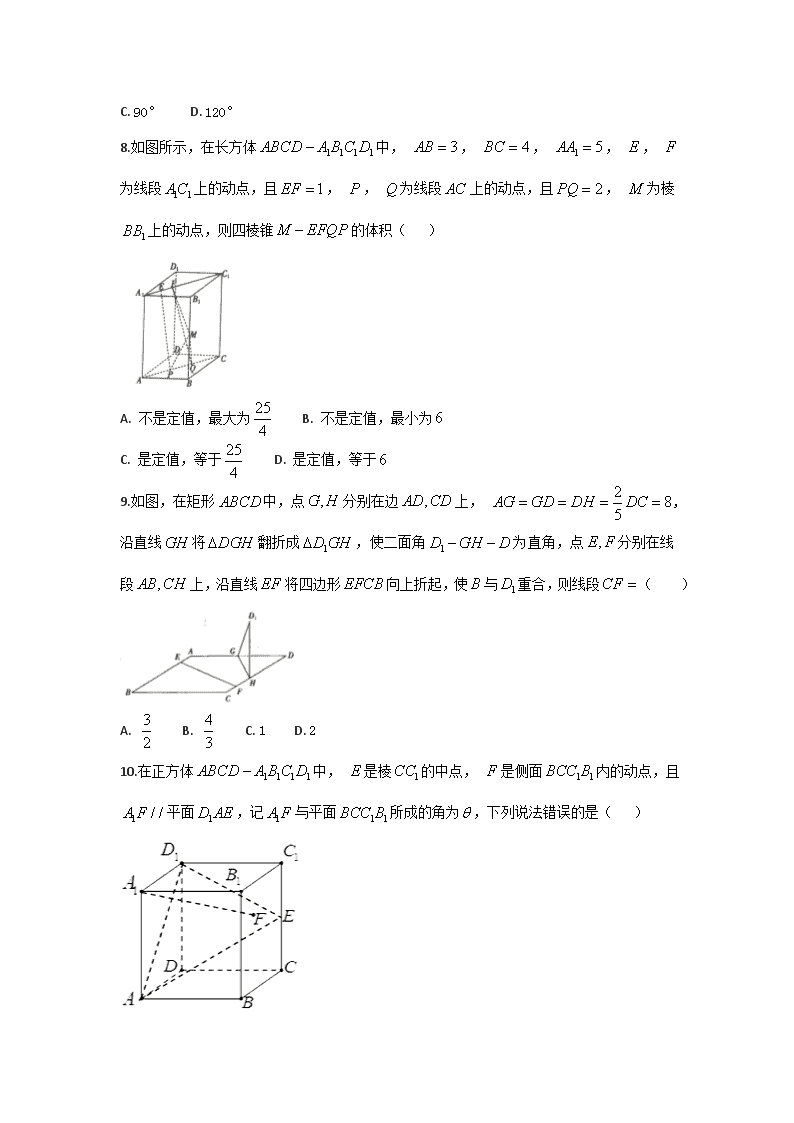
5.如图是一个几何体的三视图,则该几何体任意两个顶点间距离的最大值是 ( )
A. B. C. 4 D. 5
6.在空间四边形ABCD中,E,F分别为AB,AD上的点,且AE∶EB=AF∶FD=1∶4,又H,G分别为BC,CD的中点,则 ( )
A. BD∥平面EFG,且四边形EFGH是平行四边形
B. EF∥平面BCD,且四边形EFGH是梯形
C. HG∥平面ABD,且四边形EFGH是平行四边形
D. EH∥平面ADC,且四边形EFGH是梯形
7.如图,面,B为AC的中点, ,且P到直线BD的距离为则的最大值为( )
A. 30° B. 60°
C. 90° D. 120°
8.如图所示,在长方体中, , , , , 为线段上的动点,且, , 为线段上的动点,且, 为棱上的动点,则四棱锥的体积( )
A. 不是定值,最大为 B. 不是定值,最小为
C. 是定值,等于 D. 是定值,等于
9.如图,在矩形中,点分别在边上, ,沿直线将翻折成,使二面角为直角,点分别在线段上,沿直线将四边形向上折起,使与重合,则线段( )
A. B. C. 1 D. 2
10.在正方体中, 是棱的中点, 是侧面内的动点,且平面,记与平面所成的角为,下列说法错误的是( )
A. 点的轨迹是一条线段 B. 与不可能平行
C. 与是异面直线 D.
11.在正三棱柱中,若,则点到平面的距离为( )
A. B. C. D.
12.如图, 是用斜二测画法画出的直观图,其中, , , 轴,则的面积为( )
A. B. C. D.
第II卷(非选择题)
二、填空题
13.如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥DQ,则a的值等于 .
14.如图为某几何体的三视图,则其体积为__________.
15.已知在直角梯形中, , , ,将直角梯形沿折成三棱锥,当三棱锥的体积最大时,其外接球的体积为__________.
16.如图,在透明塑料制成的长方体容器内灌进一些水,将容器底面一边
固定于地面上,再将容器倾斜,随着倾斜角度的不同,有下列四个说法:
①水的部分始终呈棱柱状;
②水面四边形的面积不改变;
③棱始终与水面平行;
④当时, 是定值.
其中正确说法是__________.
三、解答题
17.在正方体ABCD﹣A1B1C1D1中,P、Q、R分别在棱AB、BB1、CC1上,且PD、QR相交于点O.求证:O、B、C三点共线.
18.在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,且△ABC为正三角形,点D是BC的中点,BC=BB1 .
(1)求证:A1C∥平面AB1
D;
(2)M为棱CC1的中点,试证明:MB⊥AB1 .
19.在三棱柱中,侧棱底面,,,。
(Ⅰ)若为线段上一点,且,求证:平面;
(Ⅱ)若分别是线段的中点,设平面将三棱柱分割成左、右两部分,记它们的体积分别为和,求。
20.如图,四棱锥中,底面是矩形, 底面, , ,点是的中点,点在边上移动.
(1)点为的中点时,试判断与平面的位置关系,并说明理由;
(2)证明:无论点在边的何处,都有.
21.如图,四棱锥的底面为平行四边形,平面平面,
,,点是线段上靠近点的三等分点.
(Ⅰ)求证: ;
(Ⅱ)若是边长为的等边三角形,求直线与平面所成角的正弦值.
22.在四棱锥中,底面是直角梯形, , , ,平面平面.
(Ⅰ)求证: 平面.
(Ⅱ)求平面和平面所成二面角(小于)的大小.
(Ⅲ)在棱上是否存在点使得平面?若存在,求的值;若不存在,请说明理由.
参考答案
1.A2.C3.D4.C5.B6.B7.B8.D9.A10.B11.B12.C
13.2
14.
15.
16.①③④
17.证明:∵QR∩PD=O,∴O∈QR且O∈PD,
∴O∈面BCC1B1且O∈面ABCD,
又面ABCD∩面BCC1B1=BC
∴O∈BC,
∴O、B、C三点共线.
18.证明:(1)连接A1B交AB1于E,
由题意知E是A1B中点,
∵点D是BC的中点,∴在△A1CB中ED是三角形的中位线,
∴ED∥A1C,
∵ED⊂平面AB1D,A1C不包含于平面AB1D,
∴A1C∥平面AB1D.
(2)∵BC=BB1 , ∴A1B1BA是菱形,∴AB1⊥A1B,
连结EM,AM,B1M,BM,A1M,
∵E是AB1中点,M是CC1中点,
∴EM⊥平面A1B1BA,∴A1C⊥EM,
∴A1C⊥平面A1
BM,
∵MB⊂平面A1BM,∴MB⊥AB1 .
19.
(Ⅰ)证明:如图所示,在平面中,过点作,与相交于点。因为,所以,所以,, ,四点在同一平面内。平面平面。由,得。,所以。,,所以,,所以,所以,即。又由底面,得。
又且平面,平面。所以平面。
(Ⅱ)解:如下图所示,当,分别是,中点时,直线与棱相交于的中点。连接,。则三角形就是平面截三棱柱的截面。
截面右侧为四棱锥。所以。又三棱柱的体积。
所以。
20.
证明:(1)当点为的中点时, 与平面平行,
在中, 、分别为、的中点, .
又平面,而平面, 平面.
(2)证明: 平面, 平面,
.又, ,
, 平面,
平面,又平面, .
又,点是的中点, .
又, 、平面,
平面.
平面, .
21.(Ⅰ)作于……①,连接,
∵平面平面,且 ,∴面.
∵,∴,∴,
又∵,∴……②
又,由①②,得面,又面,∴.
(Ⅱ)∵是边长为的等边三角形,
∴如图建立空间坐标系,
设面的法向量为,
,令,得
,
,设与面所成角为
∴直线与平面所成角的正弦值.
22.
(Ⅰ)∵,
∴,
∵面面,面面, 面,
∴面.
(Ⅱ)取的中点,连接,
∵,∴,
∵面面,面 , 面,
∴面,以为原点, 所在的直线为轴,在平面内过且垂直于的直线为轴, 所在的直线为轴建立空间直角坐标系,如图所示,
不妨设,由,
∴, , .
∴, .
设平面的法向量为,
∵,
∴,
令,则, .
∴.
取平面的一个法向量,
∴.
∴面和面的二面角(锐角)的大小为.
(Ⅲ)在棱上存在一点使得面,此时.
理由如下: 为的中点,
取的中点,连接, , ,
则, ,
∵,
∴,
∵,
∴四边形是平行四边形.
∴,
∵, ,
∴面面,
∵面,
∴面.