2011初三数学二模题-延庆 8页

初中数学能力测试（九）‎ 第Ⅰ卷 (选择题 32分)‎ 一、选择题：（共8个小题，每小题4分, 共32分）‎ 在下列每小题给出的四个选项中，只有一个是符合题目要求的，请在答题纸上将所选项涂黑。‎ ‎1．的倒数是 ‎ A． B． C． D． ‎ ‎2．大量事实证明，治理垃圾污染刻不容缓．据统计，全球每分钟约有吨污水排入江河湖海，这个排污量用科学记数法表示是 ‎ A．吨 B．吨 C．吨 D．吨 ‎3．若两圆的半径分别是和，圆心距为，则这两圆的位置关系是 ‎ A．内切 B．相交 C．外切 D．外离 ‎4．不等式组 的解集是 ‎ A．－＜x≤2 B．－3＜x≤‎2 C．x≥2 D．x＜－3‎ ‎5．为了解居民节约用水的情况，增强居民的节水意识，下表是某个单元的住户当月用水量的调查结果：‎ 住户（户）‎ ‎2‎ ‎4‎ ‎5‎ ‎1‎ 月用水量（方/户）‎ ‎2‎ ‎4‎ ‎6‎ ‎10‎ ‎ ‎ 则关于这12户居民月用水量(单位:方)，下列说法错误的是 ‎ ‎ A．中位数是 B．众数是 C．极差是 D．平均数是 ‎ 第6题图 C A B O E D ‎6．如图，是⊙的直径，弦于点,,‎ ‎ ⊙的半径为，则弦的长为 ‎ A． B． ‎ ‎ C． D． ‎7．从～这九个自然数中作任取一个，是的倍数的概率是 A． B． C． D．‎ ‎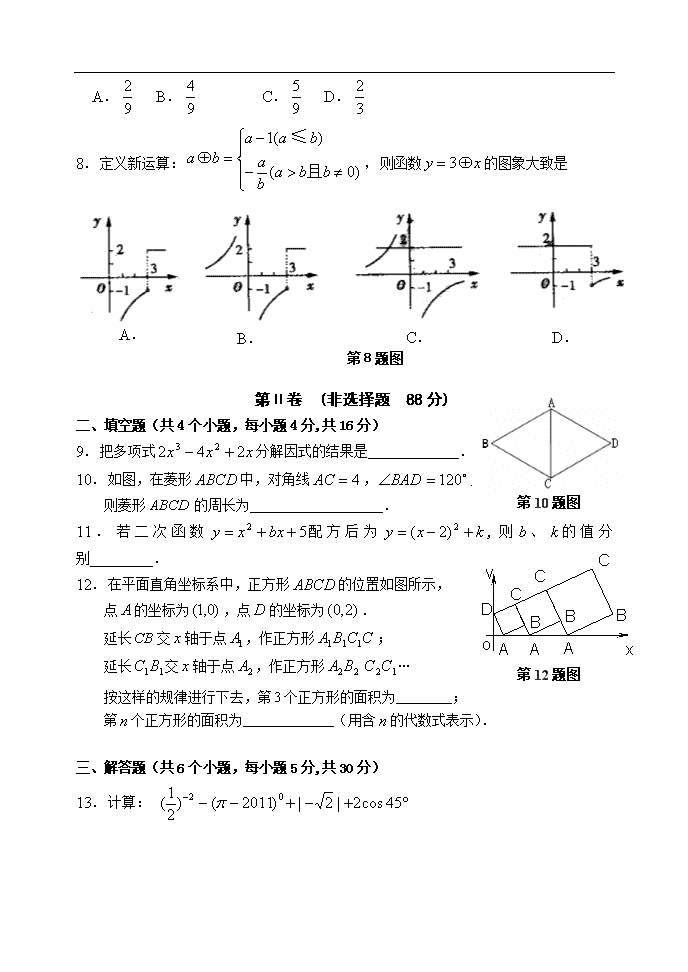8．定义新运算：，则函数的图象大致是 D．‎ 第8题图 C．‎ B．‎ A．‎ 第10题图 第Ⅱ卷 (非选择题 88分)‎ 二、填空题（共4个小题，每小题4分,共16分）‎ ‎9．把多项式分解因式的结果是 ．‎ ‎10．如图，在菱形中，对角线，，‎ ‎ 则菱形的周长为 ． ‎ y o x A A1‎ A2‎ B1‎ B B2‎ C2‎ C1‎ C D 第12题图 ‎11．若二次函数配方后为,则、的值分别 ．‎ ‎12．在平面直角坐标系中，正方形的位置如图所示，‎ 点的坐标为，点的坐标为．‎ 延长交轴于点，作正方形；‎ 延长交轴于点，作正方形…‎ 按这样的规律进行下去，第个正方形的面积为________；‎ ‎ 第个正方形的面积为_____________（用含的代数式表示）． ‎ 三、解答题（共6个小题，每小题5分,共30分）‎ ‎13．计算： ‎ ‎14．解方程：+ =1‎ ‎15．如图，中，，点在上，于点,‎ 第15题图 ‎，‎ 求证:‎ ‎16．先化简：，并从，，中选一个合适的数作为的值代入求值．‎ 第17题图 ‎17．已知：如图，一次函数与反比例函数的图象在第一象限的交点为．‎ ‎ （1）求与的值；‎ ‎ （2）设一次函数的图像与轴交于点，‎ 连接，求的度数．‎ ‎ ‎ 第17题图 ‎18．列方程或方程组解应用题：‎ 为了有效的使用电力资源，电业局对峰谷用电进行试点：每天--，用电 价格是在原电价的基础上每千瓦时上浮元（称“峰电”价），--次日，用电价格是在原电价的基础上每千瓦时下浮元（称“谷电”）。小林家在月份使用“峰电”,使用“谷电”，按分段电价付电费元，‎ ‎（1）问小林家该月支付的峰电、谷电价每千瓦时各是多少元？‎ ‎（2）如不使用分段电价结算，月份小林家将多支付电费多少元？‎ ‎ ‎ 四、解答题（共4个小题，第19，20题各5分，第21题6分，第22题4分，共20分）‎ ‎19．如图，在梯形中，，，，，‎ ‎ ，是腰上一个动点（不含点），作交于点（图）‎ ‎（1）求的长与梯形的面积；‎ 第19题图2‎ 第19题图1‎ ‎（2）当时，求的长；（图）‎ ‎20．如图，为的直径，劣弧 ，，‎ 第20题图 连接并延长交于．‎ 求证：（1）是的切线；‎ ‎（2）若的半径为,,求．‎ ‎21．四中的一个数学兴趣小组在本校学生中开展主题为“垃圾分类知多少”的专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，划分等级后的数据整理如下表：‎ 等级 非常了解 比较了解 基本了解 不太了解 频数 频率 ‎（1）本次问卷调查取样的样本容量为_______，‎ 表中的值为_______；值为_______．‎ ‎ （2）根据表中的数据计算等级为“非常了解”的频数 在扇形统计图所对应的扇形的圆心角的度数，‎ 并补全扇形统计图；‎ ‎ （3）若该校有学生人，请根据调查结果估计这些 学生中“比较了解”垃圾分类知识的人数约为多少？‎ ‎22．阅读材料：‎ ‎ （1）操作发现:‎ ‎ 如图，矩形中，是的中点，将△沿折叠后得到，且点 在矩形内部．小明将延长交于点，‎ ‎ 认为，你同意吗？说明理由．‎ ‎（2）问题解决:‎ ‎ 保持（1）中的条件不变，若，求的值；‎ ‎（3）类比探求:‎ ‎ 保持（1）中条件不变，若，求的值．‎ 五、解答题（共3个小题， 23小题7分，24小题8分，25小题7分，共22分）‎ ‎23．已知关于函数 ‎（1）若此函数的图像与坐标轴只有个交点，求的值.‎ ‎（2）求证：关于的一元二次方程必有一个根是.‎ ‎24．已知抛物线（）与轴相交于点，顶点为.直线分别与轴，轴相交于两点，并且与直线相交于点.‎ ‎ （1）填空：试用含的代数式分别表示点与的坐标，则 ； ‎ ‎ （2）如图1，将沿轴翻折，若点的对应点′恰好落在抛物线上，‎ ‎′与轴交于点，连结，求的值和四边形的面积；‎ ‎（3）在抛物线（）上是否存在一点，使得以为顶点的四边形是平行四边形？若存在，求出点的坐标；若不存在，试说明理由.‎ 第24题图1‎ x y B C O D A M N N′‎ x y B C O A M N 备用图 ‎25．如图（1），（2）所示，矩形的边长，，点在上，‎ ‎.动点分别从点同时出发，沿射线、线段向点的方向运动（点可运动到的延长线上），当动点运动到点时，两点同时停止运动．连结，‎ 当不在同一条直线时，可得，过三边的中点作．设动点的速度都是个单位／秒，运动的时间为秒．试解答下列问题：‎ ‎（1）说明∽；‎ ‎（2）设（即从到运动的时间段）．试问为何值时，为直角三角形？当在何范围时，不为直角三角形？‎ ‎（3）问当为何值时，线段最短？求此时的值．‎ 第25题图2‎ 第25题图1‎