- 165.50 KB
- 2024-02-23 发布
7.4 认识三角形(2)
【学习目标】1. 知道三角形高、中线、角平分线的定义;2.会画出任意三角形高、中线、角平分线.
【预习研问】
A 1.过点A做BC的垂线,垂足为D
A 2.在三角形中,从 向 作垂线, 和 之间的线段叫做三角形的高线,简称 。
A 3.在三角形中, 与 相交,这个角的
与 之间的线段叫做三角形的角平分线。
A 4.在三角形中,连接 和 的线段叫做三角形的中线。
A 5.已知:如图△ABC.试作△ABC的:①高AD;②角平分线BE;③中线CH.
A
C
B
A 6.下列说法正确的是 ( )
A.三角形的角平分线、中线、高都在三角形的内部
B.直角三角形只有一条高
C.三角形的三条高至少有一条在三角形内
D.钝角三角形的三条高均在三角形外
A 7.如图,AD、CE分别是△ABC的中线和高.若∠B=35°,BC=12cm,
则BD= cm, ∠BCE= .
2
F
D
C
B
A
1
E
B 8.如图,D是△ABC的边BC上一点,过点D作DE∥AC交AB于E点,
作DF∥AB交AC于F点,若∠1=∠2,则AD是△ABC的角平分线吗?
为什么?
个人或小组的预习未解决问题:
【课内解问】
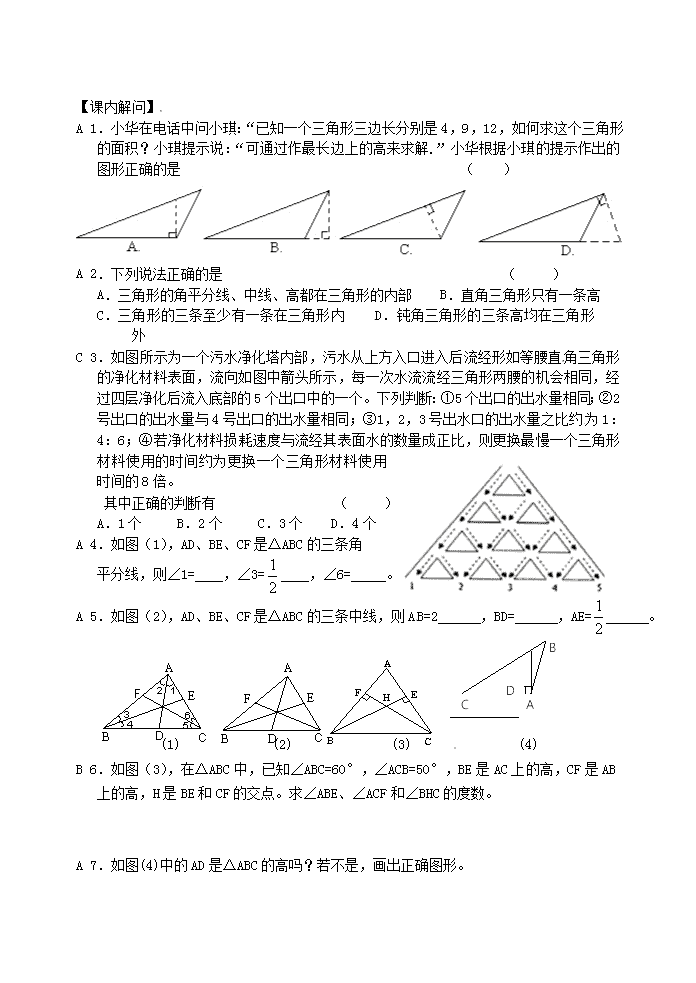
A 1.小华在电话中问小琪:“已知一个三角形三边长分别是4,9,12,如何求这个三角形的面积?小琪提示说:“可通过作最长边上的高来求解.”小华根据小琪的提示作出的图形正确的是 ( )
A 2.下列说法正确的是 ( )
A.三角形的角平分线、中线、高都在三角形的内部 B.直角三角形只有一条高
C.三角形的三条至少有一条在三角形内 D.钝角三角形的三条高均在三角形外
C 3.如图所示为一个污水净化塔内部,污水从上方入口进入后流经形如等腰直角三角形的净化材料表面,流向如图中箭头所示,每一次水流流经三角形两腰的机会相同,经过四层净化后流入底部的5个出口中的一个。下列判断:①5个出口的出水量相同;②2号出口的出水量与4号出口的出水量相同;③1,2,3号出水口的出水量之比约为1:4:6;④若净化材料损耗速度与流经其表面水的数量成正比,则更换最慢一个三角形材料使用的时间约为更换一个三角形材料使用时间的8倍。
其中正确的判断有 ( )
A.1个 B.2个 C.3个 D.4个
A 4.如图(1),AD、BE、CF是△ABC的三条角
平分线,则∠1= ,∠3= ,∠6= 。
D
A 5.如图(2),AD、BE、CF是△ABC的三条中线,则AB=2 ,BD= ,AE= 。
B
C
A
(1) (2) (3) (4)
B 6.如图(3),在△ABC中,已知∠ABC=60°,∠ACB=50°,BE是AC上的高,CF是AB上的高,H是BE和CF的交点。求∠ABE、∠ACF和∠BHC的度数。
A 7.如图(4)中的AD是△ABC的高吗?若不是,画出正确图形。
【课后答问】
A 1.三角形的角平分线是 ( )
A.直线 B.射线 C.线段 D.以上都不对
A 2.等边三角形三边上的中线,高,角平分线共有 ( )
A.3条 B.5条 C.7条 D.9条
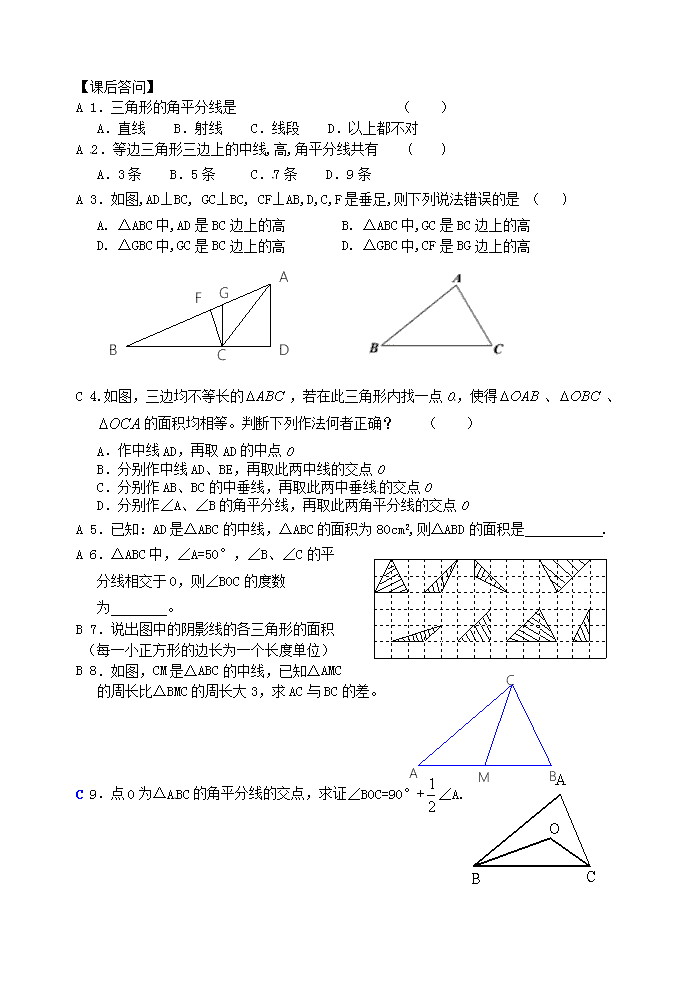
A 3.如图,AD⊥BC, GC⊥BC, CF⊥AB,D,C,F是垂足,则下列说法错误的是 ( )
A. △ABC中,AD是BC边上的高 B. △ABC中,GC是BC边上的高
D. △GBC中,GC是BC边上的高 D. △GBC中,CF是BG边上的高
A
B
D
C
F
G
C 4.如图,三边均不等长的,若在此三角形内找一点O,使得、、的面积均相等。判断下列作法何者正确? ( )
A.作中线AD,再取AD的中点O
B.分别作中线AD、BE,再取此两中线的交点O
C.分别作AB、BC的中垂线,再取此两中垂线的交点O
D.分别作∠A、∠B的角平分线,再取此两角平分线的交点O
A 5.已知:AD是△ABC的中线,△ABC的面积为80cm2,则△ABD的面积是 .
A 6.△ABC中,∠A=50°,∠B、∠C的平
分线相交于O,则∠BOC的度数
为 。
B 7.说出图中的阴影线的各三角形的面积
(每一小正方形的边长为一个长度单位)
B
C
M
A
B 8.如图,CM是△ABC的中线,已知△AMC
的周长比△BMC的周长大3,求AC与BC的差。
C 9.点O为△ABC的角平分线的交点,求证∠BOC=90°+∠A.