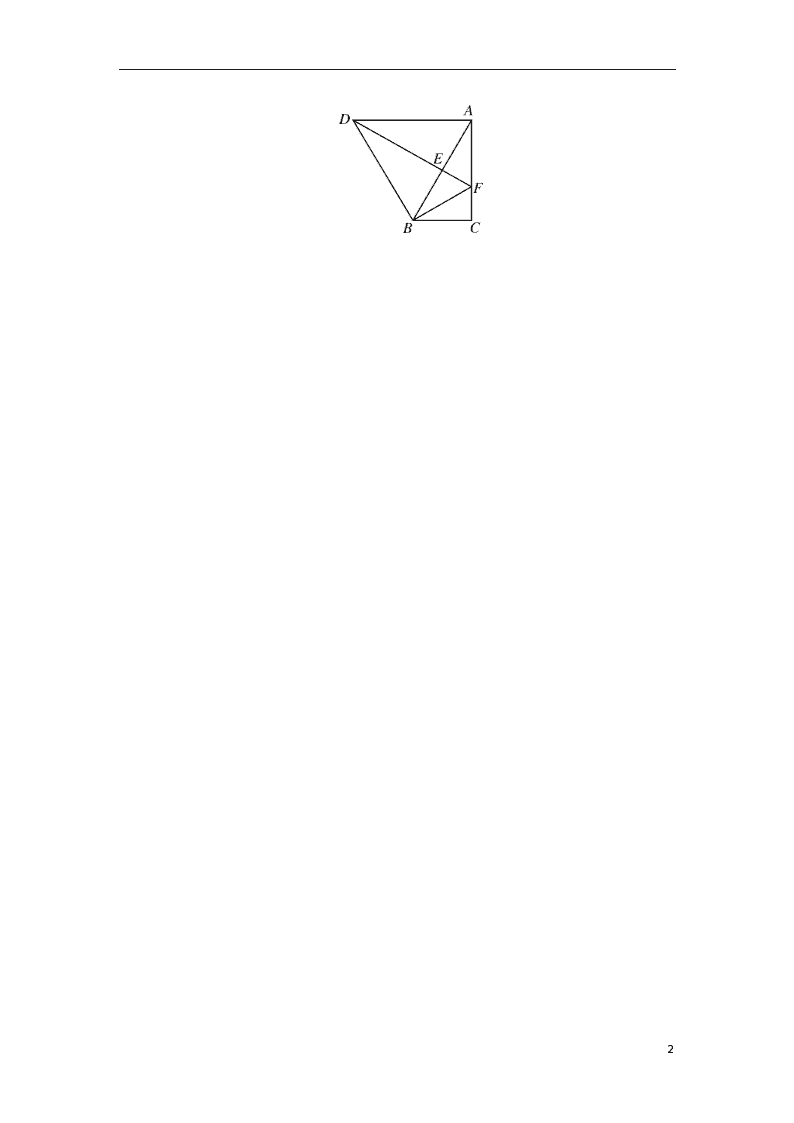2020九年级数学上册 第23章 旋转章末复习随堂检测 （新版）新人教版 3页

‎23 章末复习 ‎1．在▱ABCD中，∠A＝70°，将▱ABCD绕顶点B顺时针旋转到▱A1BC1D1，当C1D1首次经过顶点C时，旋转角∠ABA1＝__________．‎ ‎2．在等边△ABC中，AB＝10，D是BC的中点，将△ABD绕点A旋转后得到△ACE，则线段DE的长度为__________．‎ ‎3.如下图，P是矩形ABCD下方一点，将△PCD绕P点顺时针旋转60°后恰好D点与A点重合，得到△PEA，连接EB，问△ABE是什么特殊三角形？请说明理由．‎ ‎4、．如下图，等腰△OBD中，OD＝BD，△OBD绕点O逆时针旋转一定角度后得到△OAC，此时正好B、D、C在同一直线上,且点D是BC的中点.‎ ‎5.如下图，将△ABC绕点B逆时针旋转α得到△DBE，DE的延长线与AC相交于点F，连接DA、BF， ∠ABC＝α＝60°，BF＝AF.(1)求证：DA∥BC；(2)猜想线段DF、AF的数量关系，并证明你的猜想．‎ 3‎ 3‎ ‎参考答案 ‎1、40°‎ ‎2、‎ ‎3、【解析】△ABE是等边三角形．‎ 由旋转性质得△PAE≌△PDC,所以PA＝PD，AE＝DC＝AB，再由∠DPA＝60°得△PAD是等边三角形，从而得∠PDC＝∠PAE＝∠PAB＝30°，所以∠EAB＝60°，得证．‎ ‎【答案】解：△ABE是等边三角形，理由如下：‎ ‎ 由旋转，得△PAE≌△PDC，∴CD＝AE，PD＝PA，∠PDC＝∠PAE，∵∠DPA＝60°，∴△PAD是等边三角形，∴∠PDA＝∠PAD＝60°，又CD＝AB，∠CDA＝∠DAB＝90°，∴∠PDC＝∠PAB＝∠PAE＝30°，∴AE＝CD＝AB，∠EAB＝∠PAB＋∠PAE＝60°，∴△ABE是等边三角形．‎ ‎4、（1）由旋转得△OAC≌△OBD，∴OC＝OD又CD＝BD＝OD，∴OC＝OD＝CD，∴△OCD是等边三角形，∴∠COD＝60°，∴旋转角为60°‎ ‎（2）∵△OAC≌△OBD，△OCD是等边三角形， ∴AC＝BD＝CD，∠OCA＝∠ODB＝180°－60°＝120°， ∴∠ACD＝∠OCA－∠OCD＝60° ∴△ACD是等边三角形，‎ ‎ ∴OD＝OC＝AC＝AD， ∴四边形ODAC是菱形．‎ ‎5、（1）由旋转得∠DBE＝∠ABC＝60°，BD＝AB， ∴△ABD是等边三角形，∴∠DAB＝60°，‎ ‎ ∴∠DAB＝∠ABC，∴DA∥BC；‎ ‎（2）DF＝2AF，证明如下：在DF上截取DG＝AF， 连接BG，则△DBG≌△ABF，∴BG＝BF， ∠DBG＝∠ABF，∴∠GBF＝∠DBE＝60°， ∴△BGF是等边三角形，∴GF＝BF＝AF，‎ ‎ ∴DF＝DG＋FG＝2AF．‎ 3‎