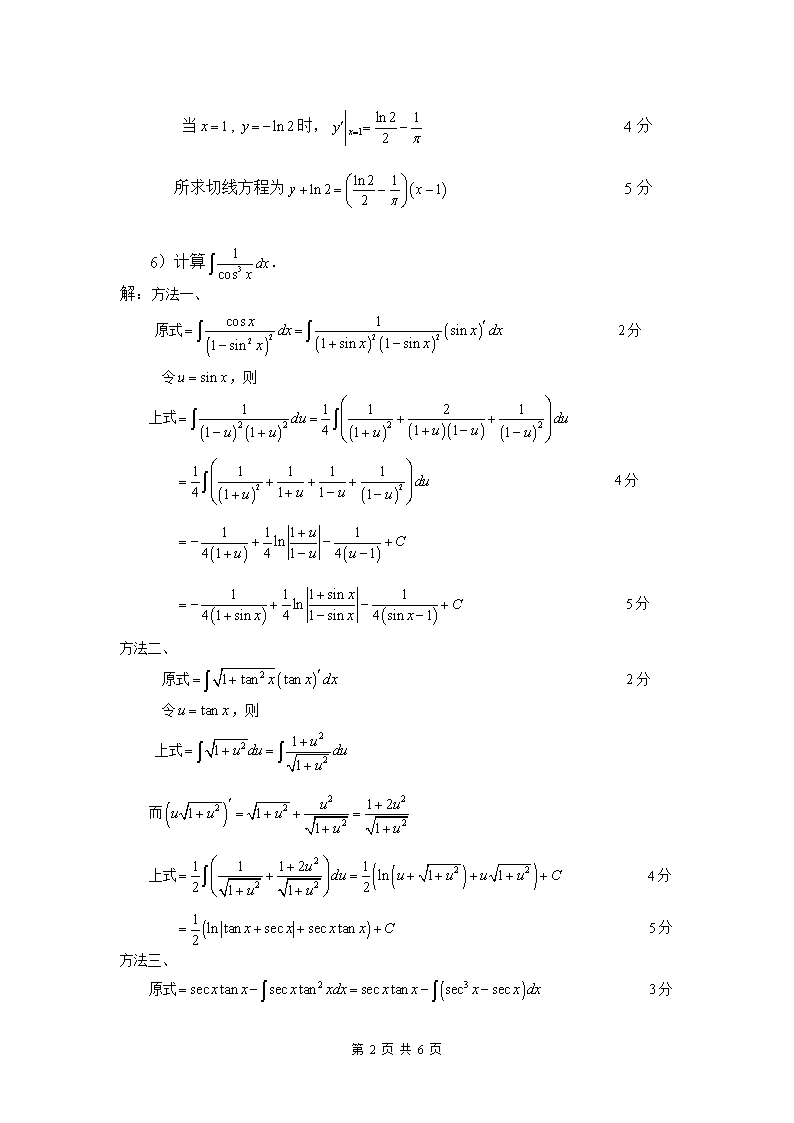- 367.00 KB
- 2021-04-12 发布
学校 姓名 考场 座位号
( 密 封 线 内 不 答 题 )
…………………………………密………………………………………………………封……………………………………………线……………………………………
第二届广东省大学生数学竞赛(经管类)
一、 计算题(每小题5分,共40分)
1).
解:原式 2分
3分
因为
所以 5分
2)设函数,求.
解:因为 3分
所以 5分
3)计算.
解:用换元法,设
原式 3分
5分
4)已知时,与是同阶无穷小,求.
解:因为 3分
所以 5分
5)设曲线由方程确定,求曲线在点处的切线方程.
解:方程两边关于求导得
3分
第 6 页 共 6 页
当时, 4分
所求切线方程为 5分
6)计算.
解:方法一、
原式 2分
令,则
上式
4分
5分
方法二、
原式 2分
令,则
上式
而
上式 4分
5分
方法三、
原式 3分
第 6 页 共 6 页
整理可得
原式
5分
7)设曲线与曲线在处相切,求.
解:由已知可得
2分
4分
5分
8)求级数的收敛域.
解:因为 2分
所以此级数收敛半径为
当时, 发散
当时,收敛 4分
所求收敛域为。 5分
二、(本题13分)证明不等式
第 6 页 共 6 页
证明:
考虑函数 4分
因为,考虑函数
当时,,且,所以当时,,又因为
所以当时,,由此可得当时,是减函数。 9分
数列是递增数列,由于时,,且
所以。 13分
三、(本题10分)设函数在上可导,在上连续,且,证明:至少存在一点使得
证明:考虑函数, 6分
由已知可得在上可导,在上连续,且,利用罗尔中值定理,至少存在一点使得
10分
第 6 页 共 6 页
四、(本题12分)设在是连续的,
1)证明:;
2)若,证明:.
证明:1)设为任意实数,因为,所以
3分
这就说明关于的一元二次方程的判别式小于或等于零,即有
5分
2)利用1)中结论证明
9分
所以
12分
五、(本题10分)讨论级数的敛散性.
解:因为 4分
8分
而收敛,所以收敛。 10分
第 6 页 共 6 页
六、(本题15分)已知函数,
1)证明:;
2)证明:;
3)若数列满足,证明
存在,并求.
解:1)因为,所以
3分
2)容易看出,所以利用拉格朗日中值定理有
6分
3)容易看出,且若,则有,所以这样
定义的数列是有意义的。利用1)和2)的结果我们有
12分
由夹逼准则得。 15分
第 6 页 共 6 页
相关文档
- 2021高考数学一轮复习第2章函数第22021-04-12 16:18:3710页
- 专题5-4 热点题型三 三角函数的2021-04-12 16:12:3210页
- 2019九年级数学上册 第二十二章 222021-04-12 16:11:492页
- 高中数学分章节训练试题:6基本初等2021-04-12 16:11:123页
- 初中数学中考总复习课件PPT:第12课2021-04-12 15:38:4738页
- 高考数学一轮复习核心素养测评十四2021-04-12 15:35:268页
- 【推荐】专题15+同角三角函数的基2021-04-12 15:14:346页
- 2019届高考数学(理)二轮复习专题透析2021-04-12 15:03:0210页
- 高等数学下册 chap2(导数与微分)2-2021-04-12 14:56:4834页
- 2019届二轮复习函数与方程思想学案2021-04-12 14:44:3611页