第5章 一次函数（知识点汇总·浙教8上） 4页

第 5 章 一次函数 一、常量和变量的概念 在一个变化过程中，可以取不同数值的量叫做变量，而数值保持不变的量叫做常量. 二、函数 1.函数的概念 在某一变化过程中，有两个量，例如 x 和 y ，对于 x 的每一个值， y 都有唯一的值与之对应，其中 x 是自变量， y 是 因变量，此时也称 y 是 x 的函数；函数不是数，它是指在一个变化过程中两个变量之间的关系，函数本质就是变量 间的对应关系。 判断 y 是 x 的函数，要抓住三个点： （1）在同一个变化过程中； （2）有两个变量； （3）一个变量的数值随另一个变量的数值的变化而变化； （4）本质上是一种对应关系，即对于每一个给定的 x 值，y 有一个唯一确定的值与之对应，否则 y 就不是 x 的函数．例 如 2y x 就不是函数，因为当 4x  时， 2y   ，即 y 有两个值与 x 对应． 对于每一个给定的 y 值， x 可以有一个 值与之对应，也可以有多个值与之对应．例如在函数 2( 3)y x  中， 2x  时， 1y  ； 4x  时， 1y  ． 2.在研究函数问题时，自变量的取值范围应注意以下两点： （1）自变量的取值要符合实际问题. 在实际问题中，自变量的取值范围应该符合实际意义，通常往往取非负数，整数之类． （2）自变量的取值要使函数表达式自身有意义. ①表达式是整式时，自变量取全体实数； ②表达式是分式时，自变量的取值要使分母不为 0； ③表达式是偶次根式时，自变量的取值必须使被开方数为非负数.表达式是奇次根式时，自变量取全体实数； ④表达式是零次幂或负整数次幂时，自变量的取值必须使底数不为零的实数． ⑤表达式是复合式时，自变量的取值是使各式成立的公共解. 3、函数的表示方法：①列表法；②解析法；③图像法 4、函数图像画法：①列表；②描点；③连线 三、一次函数 1、一次函数的概念 一般地，形如 y kx b  （ k ， b 是常数， 0k  ）的函数，叫做一次函数，特别的，当 0b  时，即 y kx ，是正比 例函数． ⑴一次函数的解析式的形式是 y kx b  ，要判断一个函数是否是一次函数，就是判断是否能化成以上形式． ⑵当 0b  ， 0k  时， y kx 仍是一次函数． ⑶当 0b  ， 0k  时，它不是一次函数． ⑷正比例函数是一次函数的特例，一次函数包括正比例函数． “正比例函数”与“成正比例”的区别： 正比例函数一定是 y=kx 这种形式，而成正比例则意义要广泛得多，它反映了两个量之间的固定正比例关系，如 a+3 与 b-2 成正比例，则可表示为：a+3=k（b-2）（k≠0） 2、一次函数的图象 ⑴一次函数 y kx b  （ 0k  ， k ， b 为常数）的图象是一条直线． ⑵由于两点确定一条直线，所以在平面直角坐标系内画一次函数的图象时，只要先描出两个点，再连成直线即可． ①如果这个函数是正比例函数，通常取  0 0， ， 1 k， 两点； ②如果这个函数是一般的一次函数（ 0b  ），通常取  0 b， ， 0b k     ， ，即直线与两坐标轴的交点． ⑶由函数图象的意义知，满足函数关系式 y kx b  的点 x y， 在其对应的图象上，这个图象就是一条直线l ，反之， 直线 l 上的点的坐标  x y， 满足 y kx b  ，也就是说，直线 l 与 y kx b  是一一对应的，所以通常把一次函数 y kx b  的图象叫做直线l ： y kx b  ，有时直接称为直线 y kx b  ． 注意：若两个不同的一次函数的一次项的系数相同，则这它们的图象平行。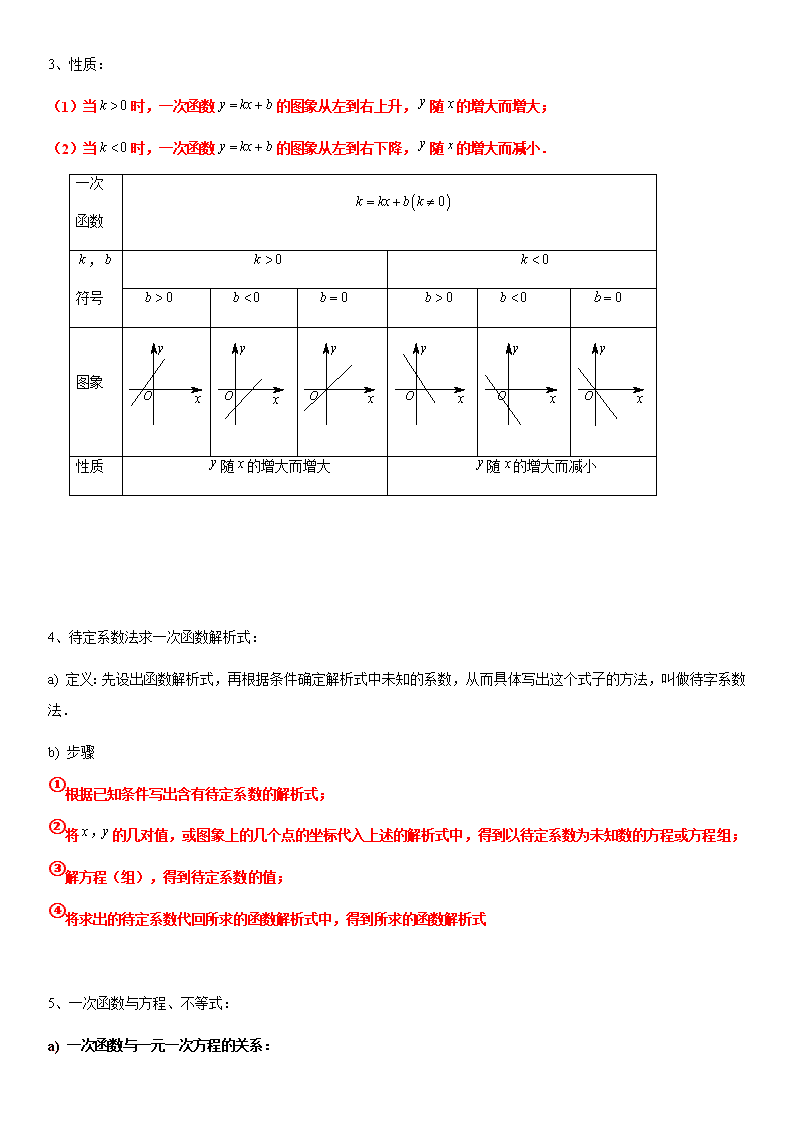 3、性质： （1）当 0k  时，一次函数 y kx b  的图象从左到右上升， y 随 x 的增大而增大； （2）当 0k  时，一次函数 y kx b  的图象从左到右下降， y 随 x 的增大而减小． 一次 函数  0k kx b k   k ，b 符号 0k  0k  0b  0b  0b  0b  0b  0b  图象 性质 y 随 x 的增大而增大 y 随 x 的增大而减小 4、待定系数法求一次函数解析式： a) 定义：先设出函数解析式，再根据条件确定解析式中未知的系数，从而具体写出这个式子的方法，叫做待字系数 法． b) 步骤 ①根据已知条件写出含有待定系数的解析式； ②将 x y， 的几对值，或图象上的几个点的坐标代入上述的解析式中，得到以待定系数为未知数的方程或方程组； ③解方程（组），得到待定系数的值； ④将求出的待定系数代回所求的函数解析式中，得到所求的函数解析式 5、一次函数与方程、不等式： a) 一次函数与一元一次方程的关系： 直线 y b k 0kx  （ ）与 x 轴交点的横坐标，就是一元一次方程 b 0( 0)kx k   的解。求直线 y bkx  与 x 轴交点 时，可令 0y  ，得到方程 b 0kx   ，解方程得 x b k   ，直线 y bkx  交 x 轴于 ( ,0)b k  ， b k  就是直线 y bkx  与 x 轴交点的横坐标。 b) 一次函数与一元一次不等式的关系： 任何一元一次不等式都可以转化为 a b 0x   或 a b 0x   ( ba、 为常数， 0a  )的形式，所以解一元一次不等式可以 看作：当一次函数值大（小）于 0 时，求自变量相应的取值范围。 c) 一次函数与二元一次方程（组）的关系： 一次函数的解析式 y b k 0kx  （ ）本身就是一个二元一次方程，直线 y b k 0kx  （ ）上有无数个点，每个点的 横纵坐标都满足二元一次方程 y b k 0kx  （ ），因此二元一次方程的解也就有无数个。 6、直线 11 bxky  （ 01 k ）与 22 bxky  （ 02 k ）位置关系 （1）两直线平行  21 kk  且 21 bb  （2）两直线相交  21 kk  （3）两直线重合  21 kk  且 21 bb  （4）两直线垂直  121 kk 7、一次函数、正比例函数图像的主要特征： 一次函数 bkxy  的图像是经过点（0，b）、（ ，0）的直线；正比例函数 kxy  的图像是经过原点（0， 0）的直线。 正比例函数 一次函数 概 念 一般地，形如 y=kx(k 是常数，k≠0)的函数 叫做正比例函数，其中 k 叫做比例系数 一般地，形如 y=kx＋b(k,b 是常数，k≠0)，那么 y 叫 做 x 的一次函数.当 b=0 时，是 y=kx，所以说正比例 函数是一种特殊的一次函数. 自变量范围 X 为全体实数 图 象 一条直线 必过点 （0，0）、（1，k） （0，b）和（- k b ，0） 走 向 k>0 时，直线经过一、三象限； k<0 时，直线经过二、四象限 k＞0，b＞0,直线经过第一、二、三象限 k＞0，b＜0 直线经过第一、三、四象限 k＜0，b＞0 直线经过第一、二、四象限 k＜0，b＜0 直线经过第二、三、四象限 增减性 k>0，y 随 x 的增大而增大；（从左向右上升） k<0，y 随 x 的增大而减小。（从左向右下降） 倾斜度 |k|越大，越接近 y 轴；|k|越小，越接近 x 轴 图像的平移 k 相同 b>0 时，将直线 y=kx 的图象向上平移 b 个单位； b<0 时，将直线 y=kx 的图象向下平移 b 个单位.