人教A版选修1-13-1空间向量及其运算第5课时（含答案） 5页

§3.1.5 空间向量运算的坐标表示 【学情分析】： 平面向量有座标表示，空间向量也有座标表示，在上一节中，单位正交分解就能够完成向量坐标向空 间直角坐标系坐标的转化。现在，通过本节的学习，我们可以将向量的地定性公式定量化，在解题特别是 在解决立体几何问题的过程中，可以大大简化问题的难度。 【教学目标】： （1）知识与技能：能用坐标表示空间向量 （2）过程与方法：由平面坐标运算类别空间坐标运算，掌握空间向量的坐标运算 （3）情感态度与价值观：类比学习，注重类比，运用向量的运算解决问题，培养学生的开拓能力。 【教学重点】： 空间向量的坐标运算 【教学难点】： 空间向量的坐标运算 【教学过程设计】： 教学环节 教学活动 设计意图 一．温故 知新 平面向量的坐标运算 二．新课 讲授 1．空间向量的直角坐标运算律 （1）若 1 2 3( , , )a a a a ， 1 2 3( , , )b b b b ，则 1 1 2 2 3 3( , , )a b a b a b a b      ， 1 1 2 2 3 3( , , )a b a b a b a b      ， 1 2 3( , , )( )a a a a R      ， （2）若 1 1 1( , , )A x y z ， 2 2 2( , , )B x y z ，则 2 1 2 1 2 1( , , )AB x x y y z z    ． 一个向量在直角坐标系中的坐标等于表示这个向量的 有向线段的终点的坐标减去起点的坐标。 注重类比学习，举一反三， 在平面向量中有坐标运 算，空间向量中也有，运 2．数量积：即 ba  = 332211 bababa  3．夹角： 1 1 2 2 3 3 2 2 2 2 2 2 1 2 3 1 2 3 cos | | | | a b a b a ba ba b a b a a a b b b               ． 4．模长公式：若 1 2 3( , , )a a a a ， 则 2 2 2 1 2 3| |a a a a a a       ． 5．平行与垂直： 1 1 2 2 3 3// , , ( )a b a b a b a b R         00 332211  bababababa 6．距离公式：若 1 1 1( , , )A x y z ， 2 2 2( , , )B x y z ， 则 2 2 2 2 2 1 2 1 2 1| | ( ) ( ) ( )AB AB x x y y z z        ， 或 2 2 2 , 2 1 2 1 2 1( ) ( ) ( )A Bd x x y y z z      ． 算规律和结论的本质是一 样的。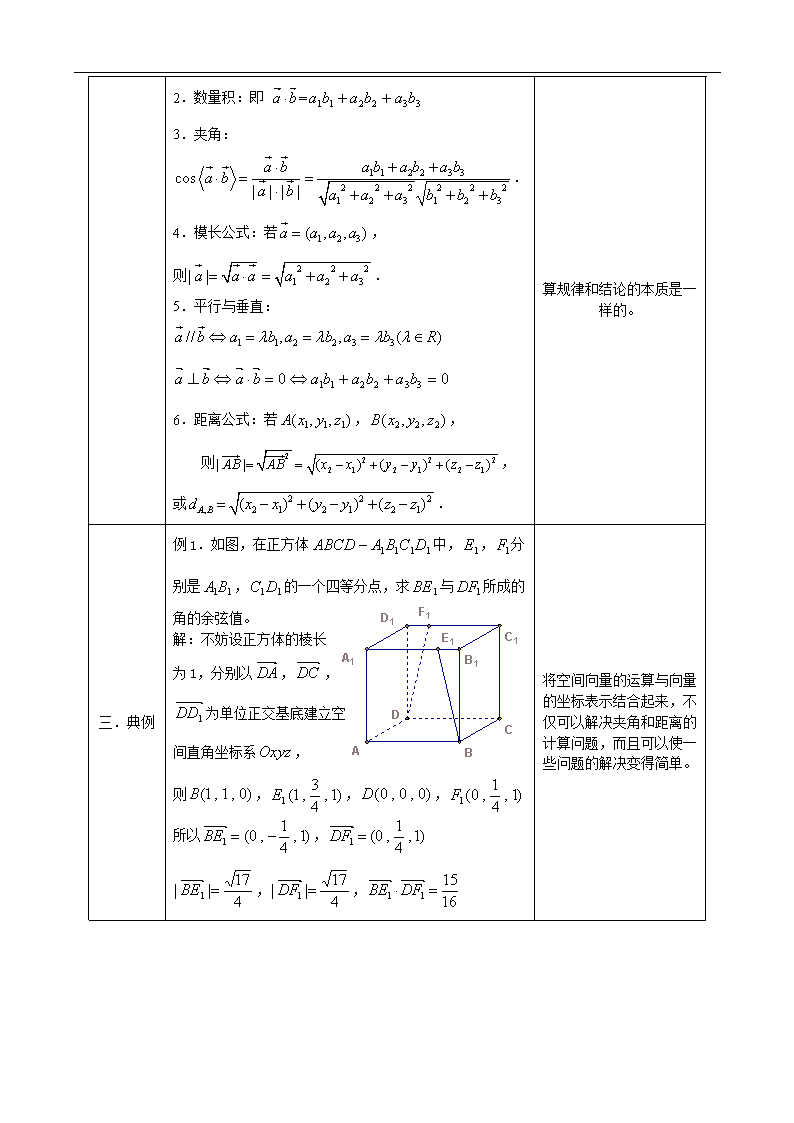 三．典例 例 1．如图，在正方体 1111 DCBAABCD  中， 1E ， 1F 分 别是 11BA ， 11DC 的一个四等分点，求 1BE 与 1DF 所成的 角的余弦值。 解：不妨设正方体的棱长 为 1，分别以 DA ， DC ， 1DD 为单位正交基底建立空 间直角坐标系Oxyz ， 则 )0,1,1(B ， )1,4 3,1(1E ， )0,0,0(D ， )1,4 1,0(1F 所以 )1,4 1,0(1 BE ， )1,4 1,0(1 DF 4 17|| 1 BE ， 4 17|| 1 DF ， 16 15 11  DFBE C 1 D 1 B 1 A 1 C D A B F 1 E 1 将空间向量的运算与向量 的坐标表示结合起来，不 仅可以解决夹角和距离的 计算问题，而且可以使一 些问题的解决变得简单。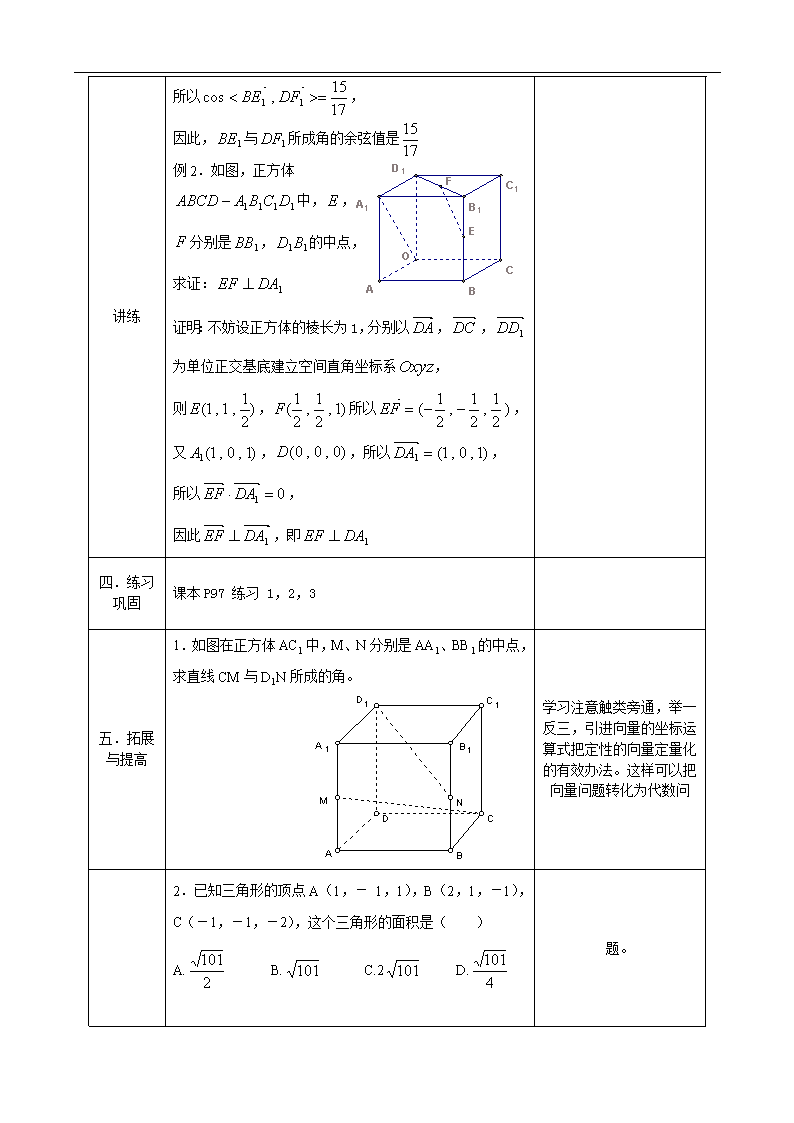 讲练 所以 17 15,cos 11  DFBE ， 因此， 1BE 与 1DF 所成角的余弦值是 17 15 例 2．如图，正方体 1111 DCBAABCD  中，E ， F 分别是 1BB ， 11BD 的中点， 求证： 1DAEF  证明：不妨设正方体的棱长为 1，分别以 DA ，DC ， 1DD 为单位正交基底建立空间直角坐标系Oxyz ， 则 )2 1,1,1(E ， )1,2 1,2 1(F 所以 )2 1,2 1,2 1( EF ， 又 )1,0,1(1A ， )0,0,0(D ，所以 )1,0,1(1 DA ， 所以 01  DAEF ， 因此 1DAEF  ，即 1DAEF  C 1 D 1 B 1 A 1 C O A B F E 四．练习 巩固 课本 P97 练习 1，2，3 五．拓展 与提高 1．如图在正方体 AC1 中，M、N 分别是 AA1、BB1 的中点， 求直线 CM 与 D1N 所成的角。 学习注意触类旁通，举一 反三，引进向量的坐标运 算式把定性的向量定量化 的有效办法。这样可以把 向量问题转化为代数问 2．已知三角形的顶点 A（1，－ 1，1），B（2，1，－1）， C（－1，－1，－2），这个三角形的面积是（ ） A. 2 101 B. 101 C.2 101 D. 4 101 题。 A B CD A 1 B 1 C1D1 NM 六．小结 1．空间向量的直角坐标运算律 2．数量积与夹角 3．模长与距离 4．平行于垂直 七．作业 课本 P98 习题 3.1，A 组 第 8、9、11 题 练习与测试： （基础题） 1．已知向量 baba 与则),2,1,1(),1,2,0(  的夹角为（ ） A．0° B．45° C．90° D．180° 2．已知 ( 1,0,2 ), (6,2 1,2),a b       // ,a b   若 则 与 的值分别为 （ ） A． 2 1,5 1 B．5，2 C． 2 1,5 1  D．-5，-2 （中等题） 3.已知 )3,1,3(A ， (1,0,5)B ，求： （1）线段 AB 的中点坐标和长度； （2）到 ,A B 两点的距离相等的点 ( , , )P x y z 的坐标 , ,x y z 满足的条件 解：（1）设 M 是线段 AB 的中点，则 )2 3,3,2()(2 1  OBOAOM ． ∴ AB 的中点坐标是 )2 3,3,2( ， )3,4,2(AB 29)3(4)2(|| 222 AB ． （2）∵ 点 ( , , )P x y z 到 ,A B 两点的距离相等， 则 222222 )0()5()1()3()1()3(  zyxzyx , 化简得： 07684  zyx , 所以，到 ,A B 两点的距离相等的点 ( , , )P x y z 的坐标 , ,x y z 满足的条件是 07684  zyx ． 点评：到 ,A B 两点的距离相等的点 ( , , )P x y z 构成的集合就是线段 AB 的中垂面，若将点 P 的坐标 , ,x y z 满足的条件 07684  zyx 的系数构成一个向量 )6,8,4( a ，发现与 )3,4,2(AB 共线。 4, 已知三角形的顶点是 (1, 1,1)A  ， (2,1, 1)B  ， ( 1, 1, 2)C    ，试求这个三角形的面积。 分析：可用公式 1 | | | | sin2S AB AC A    来求面积 解：∵ (1,2, 2)AB   ， ( 2,0, 3)AC    ， ∴ 2 2 2| | 1 2 ( 2) 3AB      ， 2 2| | ( 2) 0 ( 3) 13AC       ， (1,2, 2) ( 2,0, 3) 2 6 4AB AC           ， ∴ 4 4 13cos cos , 39| | | | 3 13 AB ACA AB AC AB AC             ， 2 13 101sin sin , 1 cos , 39A AB AC AB AC           ∴所以 1 101| | | | sin2 2ABCS AB AC A      ． 5．已知 (cos ,1,sin ), (sin ,1,cos )a b      ，则向量 a b  与 a b  的夹角是 （ ） A．90° B．60° C．30° D．0° 6．已知 (1 ,1 , ), (2, , )a t t t b t t     ，则| |a b  的最小值是 （ ） A． 5 5 B． 55 5 C． 3 5 5 D．11 5 7．已知    3cos ,3sin ,1 2cos ,2sin ,1P     和Q ，则 PQ 的取值范围是（ ） A. 0,5 B. 0,25 C. 1,5 D. 1,5