- 106.00 KB
- 2021-05-21 发布
第三单元——三角形——全等三角形
教学目标:
1、 理解全等三角形的概念;
2、 掌握全等三角形的性质和判定方法,能运用全等三角形的性质及判定定理证明两条线段相等和两个角相等;
3、 掌握两个直角三角形全等的特殊方法。
教学重点:
全等三角形的性质和判定方法
教学难点:
全等三角形的性质和判定方法的灵活应用。
例题探讨:
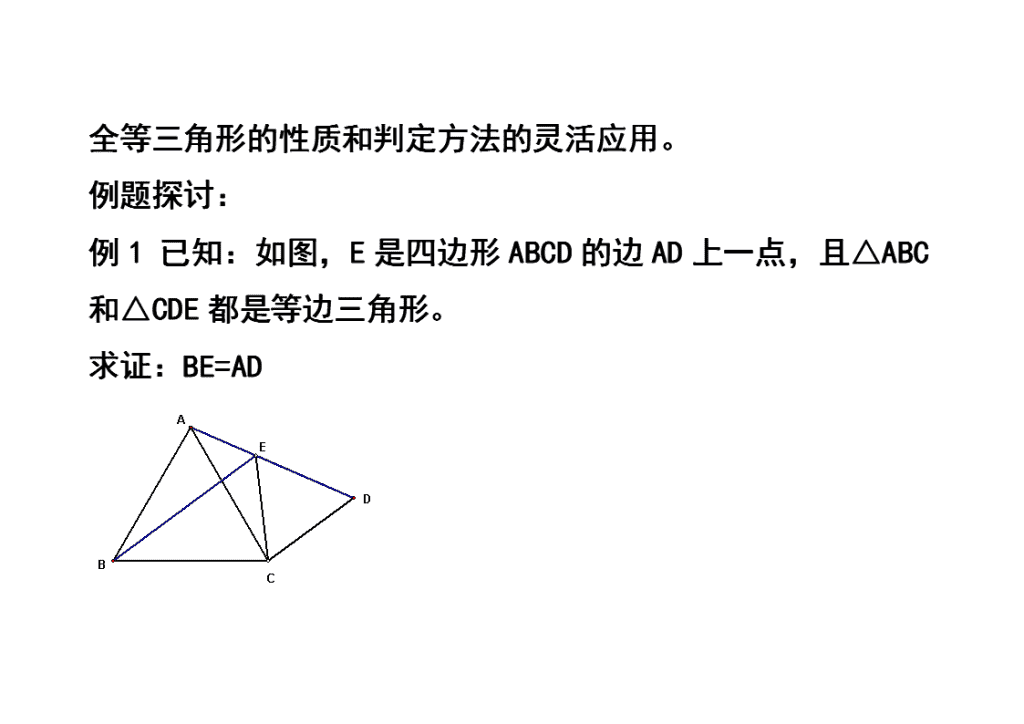
例1 已知:如图,E是四边形ABCD的边AD上一点,且△ABC和△CDE都是等边三角形。
求证:BE=AD
(补充)两个等边三角形ABC和ADE,初始时点D在AB上,点E在AC上,当△ADE绕着点A旋转且旋转角小于180°时,BD和CE的长度有什么关系?证明你的结论。
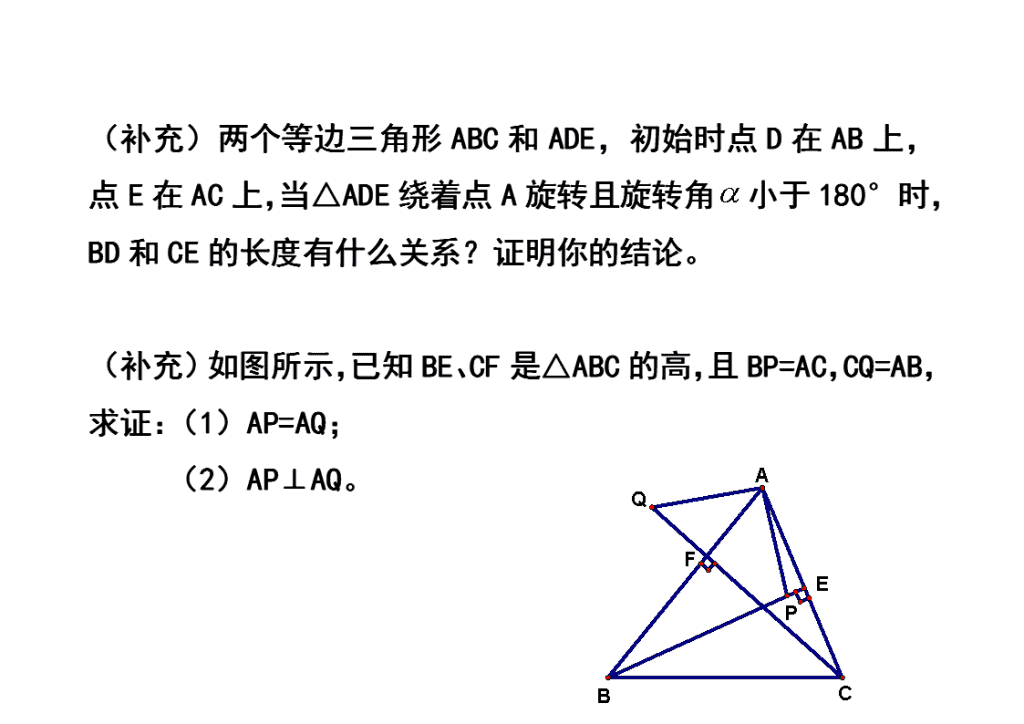
(补充)如图所示,已知BE、CF是△ABC的高,且BP=AC,CQ=AB,
求证:(1)AP=AQ;
(2)AP⊥AQ。
例2 已知:如图,在△ABC中,DE∥BC,M是边BC的中点,DM=EM。求证:∠B=∠C。
(补充)如图所示,∠CAD和∠CBD都是直角,M是CD的中点,N是AB的中点,求证:直线MN是AB的垂直平分线。
例3 如图,已知直角三角形ABC中,∠C=90°,AD平分∠A,交边BC于点D,AB=10,AC=6,求点D到边AB的距离。
(补充)如图所示,已知D是△ABC的边BC上一点,且CD=AB,
∠BDA=∠BAD,AE是△ABD的中线,求证:∠C=∠BAE。
(补充)
如图所示,把长方形ABCD的一边AB沿直线AP对折过来,使点B落在边CD上的点E处,已知AB=15cm,BC=12cm,求折痕线段AP的长。
例4 已知△ABC中,∠A=90°AB=AC, D为BC的中点。
(1) 如图,E、F分别是AB、AC上的点,且BE=AF,求证:△DEF是等腰直角三角形。
(2) 如果E、F分别是AB、CA的延长线上的点,且BE=AF,那么△DEF是否仍为等腰直角三角形?证明你的结论。
(补充)如图所示,△ABC中,AB=AC,∠A=36°,试用直线段将△ABC分割成三个等腰三角形(要求画出三种以上不同的分割法)
相关文档
- 2020届一轮复习人教A版创新思维政2021-05-21 19:28:037页
- 高考物理江苏专版一轮复习课时检测2021-05-21 19:27:546页
- 【数学】2021届一轮复习人教A版直2021-05-21 19:27:445页
- 四年级上册数学课件-3 观察物体丨2021-05-21 19:27:3414页
- 世纪金榜2016高考地理一轮复习 区2021-05-21 19:27:227页
- 2020版一年级数学下册四100以内的2021-05-21 19:27:2014页
- 广西玉林市防城港市中考物理试题wo2021-05-21 19:27:0022页
- 2019届高三二轮复习文学类文本阅读2021-05-21 19:26:365页
- 七年级下册数学课件《平行线的性质2021-05-21 19:26:2519页
- 福建省厦门湖滨中学2019-2020学年2021-05-21 19:26:2310页