高一数学必修3课件-1程序框图 24页

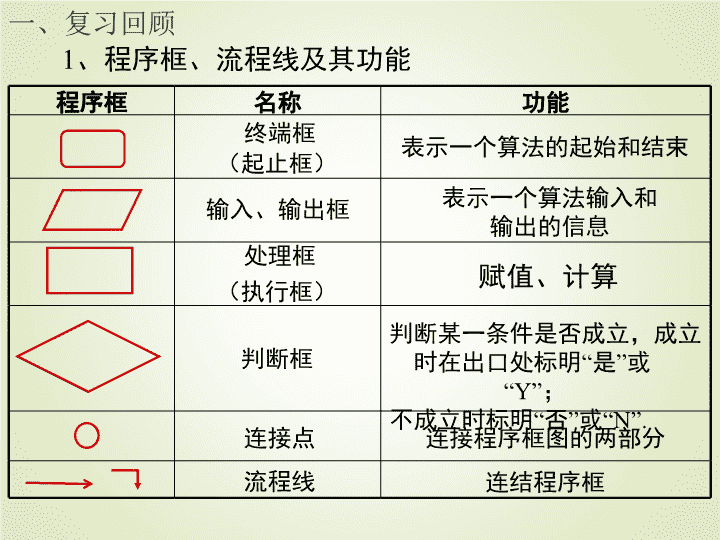
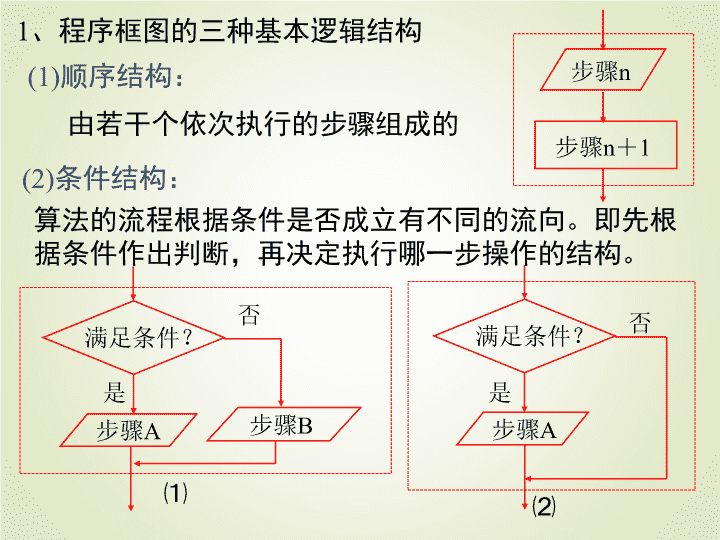
程序框 名称 功能 终端框 （起止框） 表示一个算法的起始和结束 输入、输出框 表示一个算法输入和 输出的信息 处理框 （执行框） 赋值、计算 判断框 判断某一条件是否成立，成立 时在出口处标明“是”或“Y”； 不成立时标明“否”或“N”. 连接点 连接程序框图的两部分 流程线 连结程序框 1、程序框、流程线及其功能 一、复习回顾 步骤n 步骤n＋1 (1)顺序结构： 由若干个依次执行的步骤组成的 1、程序框图的三种基本逻辑结构 (2)条件结构： 算法的流程根据条件是否成立有不同的流向。即先根 据条件作出判断，再决定执行哪一步操作的结构。 ⑴ 步骤A 步骤B 满足条件？ 否 是 步骤A 满足条件？ 否 是 ⑵ 开始 输入 的值, ,a b h 1 ( ) 2 S a b h  结束 输出S 开始 输入实数 x 3?x  5 1.2 ( 3)m x   是 m=5 否 输出m 结束 开始 i=1 3 100?i  i=i+1 是 输出i-1 结束 否 (1) (2) (3) 一、复习回顾 试判断下列流程图分别属于哪种结构的？ (3)循环结构： 在算法中，出现从某处开始，按照一定的条件反复 执行某些步骤的情况。反复执行的步骤被称为循环体 直到型循环结构当型循环结构 二、基础知识讲解 2、程序框图的三种基本逻辑结构 循环体 满足条件？ 否 是 循环体 是 否 满足条件？ (3)循环结构： 循环体 满足条件？ 否 是 循环体 是 否 满足条件？ 直到型循环结构当型循环结构 二、基础知识讲解 2、程序框图的三种基本逻辑结构 当型循环结构先对条件判断，根据结果决定是否 执行循环体； 直到型循环结构先执行一次循环体，再对一些条 件进行判断，决定是否继续执行循环体. 都包含条件结构 第1步：0+1=1 第2步：1+2=3 第3步：3+3=6 第4步：6+4=10 …… 第100步：4950+100=5050 规律： 第i 步：S=S+i S=0，i=1 第1步：S=S+i， 第2步：S=S+i， 第3步：S=S+i， 第4步：S=S+i， …… 第100步：S=S+i i=i+1 i=i+1 i=i+1 i=i+1 S=S + i i = i + 1 ，i=i+1 循环步骤： 例1、设计一个计算1+2+3+ …+100的值的算法，并画 出程序框图。 三、例题分析 例1、设计一个计算1+2+3+ …+100的值的算法，并画 出程序框图。 算法分析： 第一步，取i=1，S=0 第三步，S=S+i。 第四步，i=i+1，后返回第二步 第二步，判断i ≤100是否成立。 若是，则执行下一步； 若否，则输出S。 结束算法。 开始 i=1 S=0 否 输出S 结束 i=i+1 S=S+i 是 三、例题分析 i≤100? 程序框图： 算法分析2： 第一步，取i=1，S=0。 第二步，S=S+i，i＝i＋1。 第三步，判断 i>100 是否成立。 若是，则输出S的值； 若否，继续执行第二步。 i>100? 开始 结束 否 输出S 是 i=1 S=0 i=i+1 S=S+i 例1、设计一个计算1+2+3+ …+100的值的算法，并画 出程序框图。 三、例题分析 程序框图： 当型 直 到 型 S：累加变量 i：计数变量 开始 i=1 S=0 否 输出S 结束 i=i+1 S=S+i 是 i≤100?i>100? 开始 结束 否 输出S 是 i=1 S=0 i=i+1 S=S+i 例1、设计一个计算1+2+3+ …+100的值的算法，并画 出程序框图。 三、例题分析 当型 直 到 型 S：累加变量 i：计数变量 开始 i=1 S=0 否 输出S 结束 i=i+1 S=S+i 是 i≤100?i>100? 开始 结束 否 输出S 是 i=1 S=0 i=i+1 S=S+i 变式2、设计一个算法，求1×2×…×99的值，并画 出程序框图 当型 直 到 型 开始 i=1 S=0 否 输出S 结束 i=i+1 S=S*i 是i≤100?i>100? 开始 结束 否 输出S 是 i=1 S=1 i=i+1 S=S*i 变式2、设计一个算法，求1×2×…×99的值，并画 出程序框图 例2、某工厂2005年的年生产总值为 200万元，技术革新后预计以后每年 的年生产总值都比上一年增长5％。 设计一个程序图，输入预计年生产总 值超过300万元的最早年份。 算法分析： 第一步，确定年份和年生产总值 第二步，计算下一年的年生产总值 第三步，判断所得的结果是否大于 300。若是，则输出该年的年份；否 则，返回第二步。 三、例题分析 程序框图： 开始 结束 n = 2005, a = 200 输出 n a > 300 ? 是 否 n = n + 1 t = 0.05 a a = a +t 开始 结束 n = 2005, a = 200 输出 n a > 300 ? 是 否 n = n + 1 t = 0.05 a a = a +t 开始 n = 2005, a = 200 结束 输出 n a ≤ 300 ? 否 是 a = a + t n = n + 1 t = 0.05 a 请将该循环结构改为当型循环 如：写出用“二分法”求方程x2－2＝0（x>0）的近似 解的算法 第一步：令f(x)=x2-2，给定精确度d 第二步：确定区间[a,b],满足f(a)f(b)<0 第四步：若f(a)f(m)<0，则含零点的区间为[a,m]，否则含零 点的区间为[m,b]，将新得到的含零点的区间仍记为[a,b] 第五步：判断[a,b]的长度是否小于d或f(m)是否等于零，若是， 则m是方程的近似解，否则返回第三步 第三步：取区间中点m=(a+b)/2 二、基础知识讲解 3、画程序框图的基本步骤 第一步：令f(x)=x2-2，给定精确度d 第二步：确定区间[a,b]，满足f(a)f(b)<0 第三步：取区间中点m=(a+b)/2 (1)算法步骤中的“第一 步”，“第二步”， “第三步”可以用顺序 结构来表示。 2 a bm  2( ) 2f x x  , d a b 输入精确度 和初始值 ( ) ( ) 0?f a f m (2)算法步骤中的 “第四步”，可以 用条件结构来表示 a m 是 否 第四步：如果f(a)f(m)<0，则含零点的区间为[a,m]，否则含零点 的区间为[m,b]，将新得到的含零点的区间仍记为[a,b] b m (3)算法步骤中的“第 五步”包含一个条件 结构，这个条件结构 与“第三步”， “第 四步”构成一个循环 结构。 第三步 第四步 输出m 是 否| | ( ) 0 a b d f m    或 ？ 第五步：判断[a,b]的长度是否小于d或f(m)是否等于零，若是， 则m是方程的近似解，否则返回第三步 (4)将各步骤的程序框 图连接起来，并画出 “开始”和 “结束” 两个终端框，就得到 了表示整个算法的程 序框图． 输出m 开始 结束 是 否 ① ① ② ② 2 a bm  2( ) 2f x x  , d a b 输入精确度 和初始值 ( ) ( ) 0?f a f m  a m 是 否 b m | | ( ) 0 a b d f m    或 ？ ⑴用自然语言表达算法步骤； ⑵确定每一个算法步骤所包含的逻辑结构，并用相 应的程序框表示，得到该步骤的程序框图； ⑶将所有步骤的程序框图用流程线连接起来，并加 上终端框，得到表示整个算法的程序框图。 二、基础知识讲解 3、画程序框图的基本步骤 1、循环结构的特点 2、循环结构的框图表示 3、循环结构有注意的问题 避免死循环的出现，设置好进入（结束） 循环体的条件。 当型和直到型 重复同一个处理过程 四、课时小结 Ø习题1.1 A组 第2题 1 1 11 2 3 s n         的值，并画出程序框图. 开始 输入一个正整数n 输入S的值 结束 S=0 i=1 S=S+1/i i=i+1 i>n? N Y 设计一个算法求 步骤A 步骤B 思考:将步骤A和步骤B交换位 置，结果会怎样？能达到预 期结果吗？为什么？要达到 预期结果，还需要做怎样的 修改？ 练习： 对任意正整数n, 【变式引申】画程序框图，求 1 1 1 1 1 11 2 3 4 5 9 10        的值. 六、思考题