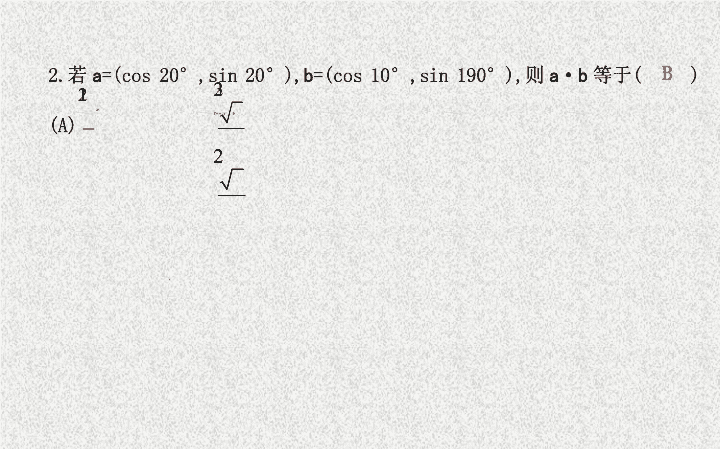2020届二轮复习简单的三角恒等变换二课件（26张） 26页

课标要求 : 掌握三角恒等变换在三角函数图象与性质中的应用 . 自我检测 B 自主学习 B C 答案 : -2sin 4 答案 : π 题型一 三角恒等变换与平面向量知识的综合 课堂探究 【 例 1】 已知向量 a =(1+sin 2x,sin x-cos x), b =(1,sin x+cos x), 函数 f(x)= a · b . (1) 求 f(x) 的最大值及相应的 x 值 ; 方法技巧 此类题的主要考查方式有两种 :(1) 三角函数与向量的数量积直接联系 ;(2) 利用三角函数与向量的夹角交汇 , 达到与数量积的综合 . 解答此类问题时应熟练掌握向量数量积运算的坐标表示 , 熟练运用向量平行、垂直的坐标运算将向量问题转化为三角函数式 , 再利用三角恒等变换对三角函数式进行化简求值等 . 即时训练 1 - 1: 已知平面向量 a =(sin x,cos x),b=(sin x,-cos x),c= (-cos x,-sin x),x∈R, 函数 f(x)= a · (b-c). (1) 求函数 f(x) 的单调递减区间 ; 题型二 三角恒等变换与三角函数的综合 题后反思 函数的解析式的次数可以降低 , 项数可以减少时 , 要先化简解析式成 y=Asin(ωx+)+B 的形式再研究其图象及性质 . 题型三 三角恒等变换的实际应用 【 例 3】 点 P 在直径 AB=1 的半圆上移动 , 过 P 作圆的切线 PT 且 PT=1,∠PAB= α, 问 α 为何值时 , 四边形 ABTP 面积最大 ? 解: 如图所示.因为AB为直径, 所以∠APB=90°,AB=1,∠PAB=α. 则PA=cos α,PB=sin α. 又PT为圆的切线, 所以∠TPB=∠PAB=α, 方法总结 应用三角函数解决实际问题的策略 一般情况下 , 引入恰当的辅助角 , 建立有关辅助角的三角函数表达式 , 并利用和、差、倍、半角公式进行化简整理 . 由于引入辅助角的恰当与否直接影响该题的计算量 , 故求解时多注意分析题意 , 恰当引入 , 提高解题能力 .