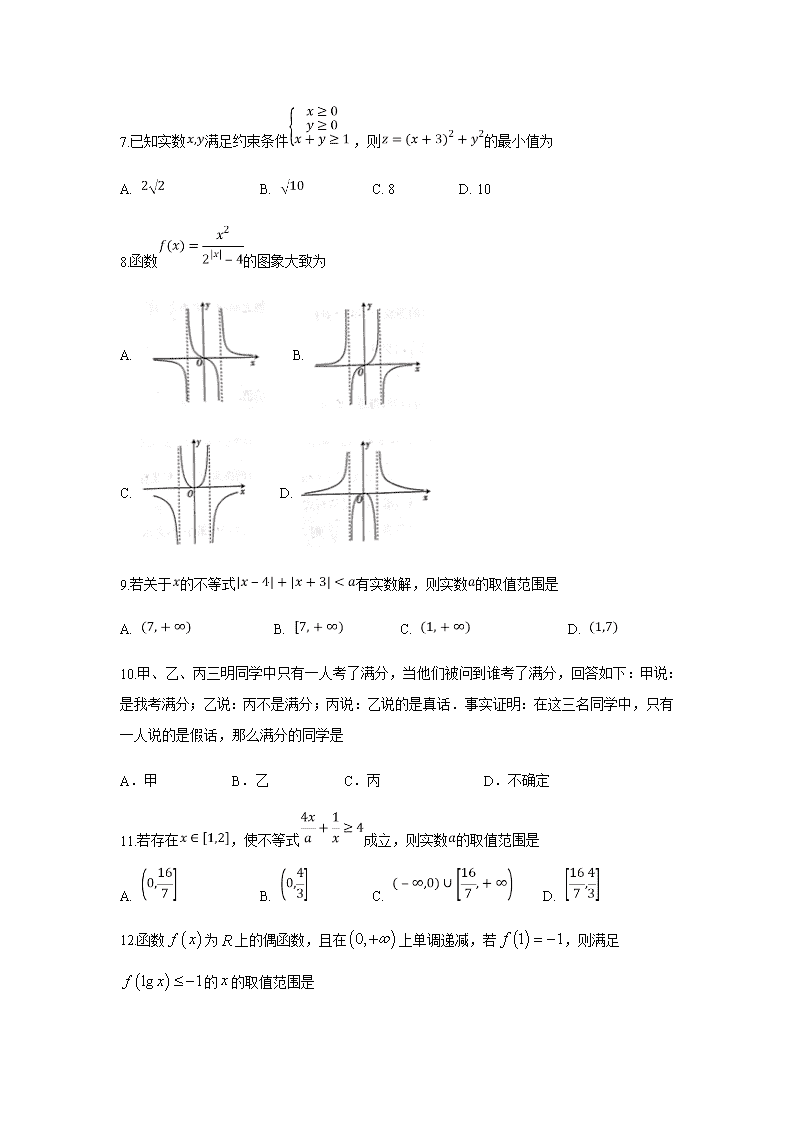【数学】四川省棠湖中学2019-2020学年高二下学期第四学月考试（文） 14页

四川省棠湖中学2019-2020学年 高二下学期第四学月考试（文）‎ 注意事项：‎ ‎1．答卷前，考生务必将自己的姓名和准考证号填写在答题卡上。‎ ‎2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。3．考试结束后，将本试卷和答题卡一并交回。‎ 第I卷 选择题（60分）‎ 一、选择题：本题共12小题，每小题5分，共60分。在每小题给的四个选项中，只有一项是符合题目要求的。‎ ‎1.若，则 ‎ A. B. C. D. ‎ ‎2.若函数，则 ‎ A. B. C. D.‎ ‎3.目前，国内很多评价机构经过反复调研论证，研制出“增值评价”方式。下面实例是某市对“增值评价”的简单应用，该市教育评价部门对本市所高中按照分层抽样的方式抽出所(其中，“重点高中”所分别记为,“普通高中”所分别记为),进行跟踪统计分析，将所高中新生进行了统的入学测试高考后，该市教育评价部门将人学测试成绩与高考成绩的各校平均总分绘制成了雷达图.点表示学校入学测试平均总分大约分，点表示学校高考平均总分大约分，则下列叙述不正确的是（ ）‎ A.各校人学统一测试的成绩都在分以上 ‎ B.高考平均总分超过分的学校有所 C.学校成绩出现负增幅现象 ‎ D.“普通高中”学生成绩上升比较明显 ‎4.在下列各函数中，最小值等于2的函数是 ‎ A. B. （） ‎ C. D. ‎ ‎5.在同一平面直角坐标系中，经过伸缩变换后，曲线变为曲线，则曲线的方程为 ‎ A. B. ‎ C. D. ‎ ‎6.已知，则 ‎ A.是的充分不必要条件 B.是的充分不必要条件 C.是的必要不充分条件 D.是的必要不充分条件 ‎7.已知实数满足约束条件，则的最小值为 ‎ A. B. C. 8 D. 10‎ ‎8.函数的图象大致为 A. B. ‎ C. D. ‎ ‎9.若关于的不等式有实数解，则实数的取值范围是 ‎ A. B. C. D. ‎ ‎10.甲、乙、丙三明同学中只有一人考了满分，当他们被问到谁考了满分，回答如下：甲说：是我考满分；乙说：丙不是满分；丙说：乙说的是真话．事实证明：在这三名同学中，只有一人说的是假话，那么满分的同学是 ‎ A．甲 B．乙 C．丙 D．不确定 ‎11.若存在，使不等式成立，则实数的取值范围是 ‎ A. B. C. D. ‎ ‎12.函数为上的偶函数，且在上单调递减，若，则满足的的取值范围是 A. B. ‎ C. D.‎ 第II卷 非选择题（90分）‎ 二、 填空题：本题共4小题，每小题5分，共20分。‎ ‎13.命题“R，”的否定为_______‎ ‎14.关于的不等式的解集是，则关于的不等式的解集是_______．‎ ‎15.如图是函数的导函数的图像，给出下列命题：‎ ‎①-2是函数的极值点；②函数在处取最小值；‎ ‎③函数在处切线的斜率小于零；④函数在区间上单调递增.‎ 则正确命题的序号是__________．‎ ‎16.已知椭圆的左、右焦点分别为，若椭圆上存在一点使得，则该椭圆的离心率的取值范围是______．‎ 三．解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。‎ ‎（一）必考题：共60分 ‎17.（12分）为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：‎ ‎ ‎ 喜爱打篮球 ‎ 不喜爱打篮球 ‎ 合计 ‎ 男生 ‎ ‎ ‎ ‎5 ‎ ‎ ‎ 女生 ‎ ‎10 ‎ ‎ ‎ ‎ ‎ 合计 ‎ ‎ ‎ ‎ ‎ ‎５０ ‎ 已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为．‎ ‎（I）请将上面的列联表补充完整；‎ ‎（II）是否在犯错误的概率不超过0.5%的前提下认为喜爱打篮球与性别有关？说明你的理由.下面的临界值表供参考：‎ ‎ ‎ ‎0.15 ‎ ‎0.10 ‎ ‎0.05 ‎ ‎0.025 ‎ ‎0.010 ‎ ‎0.005] ‎ ‎0.001 ‎ ‎ ‎ ‎2.072 ‎ ‎2.706 ‎ ‎3.841 ‎ ‎5.024 ‎ ‎6.635 ‎ ‎7.879 ‎ ‎10.828 ‎ ‎(参考公式：，其中)‎ ‎18.（12分）如图,棱形的边长为6, ,.将棱形沿对角线折起,得到三棱锥,点是棱的中点, .‎ ‎（Ⅰ）求证：∥平面;‎ ‎（Ⅱ）求三棱锥的体积.‎ ‎19.（12分）某幼儿园雏鹰班的生活老师统计2018年上半年每个月的20日的昼夜温差，和患感冒的小朋友人数（/人）的数据如下：‎ 温差 患感冒人数 ‎8‎ ‎11‎ ‎14‎ ‎20‎ ‎23‎ ‎26‎ 其中，，.‎ ‎（Ⅰ）请用相关系数加以说明是否可用线性回归模型拟合与的关系；‎ ‎（Ⅱ）建立关于的回归方程（精确到），预测当昼夜温差升高时患感冒的小朋友的人数会有什么变化？（人数精确到整数）‎ 参考数据：．参考公式：相关系数：，回归直线方程是， ,‎ ‎20.（12分）已知椭圆： 的离心率为，短轴一个端点到右焦点的距离为 ‎（I）求椭圆的方程；‎ ‎（II）设直线与椭圆交于，两点，坐标原点到直线的距离为，求面积的最大值.‎ ‎21.（12分）已知函数，（）．‎ ‎（I）若恒成立，求实数的取值范围；‎ ‎（II）已知，是函数的两个零点，且，求证：．‎ ‎（二）选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题计分。‎ ‎22．[选修4-4：坐标系与参数方程]（10分）‎ 在平面直角坐标系中,直线的参数方程为参数),以原点为极点,轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.‎ ‎（Ⅰ）求曲线的直角坐标方程和直线的普通方程；‎ ‎（II）若与交于两点，设，求.‎ ‎23．[选修4-5：不等式选讲]（10分）‎ 已知函数 ‎（Ⅰ）解不等式；‎ ‎（Ⅱ）对及，不等式恒成立，求实数的取值范围.‎ 参数答案 ‎1.D 2.C 3.B 4.D 5.B 6.D 7.D 8.D 9.A 10.B 11.A 12.C ‎13.， 14. 15.①④ 16.‎ ‎17.试题解：(1) 列联表补充如下： ‎ ‎ ‎ 喜爱打篮球 ‎ 不喜爱打篮球 ‎ 合计 ‎ 男生 ‎ ‎２０ ‎ ‎５ ‎ ‎２５ ‎ 女生 ‎ ‎１０ ‎ ‎１５ ‎ ‎２５ ‎ 合计 ‎ ‎３０ ‎ ‎２０ ‎ ‎５０ ‎ ‎（2）∵ ‎ 在犯错误的概率不超过0.5%的前提下认为喜爱打篮球与性别有关 ‎ ‎18.（１）证明：因为点是菱形的对角线的交点，‎ 所以是的中点.又点是棱的中点，‎ 所以是的中位线，. 2分 因为平面,平面， 4分 所以平面. 6分 ‎（２）三棱锥的体积等于三棱锥的体积. 7分 由题意，,‎ 因为,所以，. 8分 又因为菱形，所以. 9分 因为,所以平面，即平面10分 所以为三棱锥的高. 11分 的面积为 ， 13分 所求体积等于 . 14分 ‎19解：(Ⅰ)，‎ ‎．‎ 故，∴可用线性回归模型拟合与的关系；‎ ‎(Ⅱ)，，，‎ ‎∴关于的回归方程为．当时，．‎ 预测当昼夜温差升高时患感冒的小朋友的人数会增加10人．‎ ‎20解：（1）设椭圆的半焦距为，依题意，所求椭圆方程为．‎ ‎（2）设，．‎ ‎①当轴时，．‎ ‎②当与轴不垂直时，设直线的方程为．‎ 由已知，得．‎ 把代入椭圆方程，整理得 ，‎ ‎，‎ ‎ ．‎ ‎ ‎ ‎ ‎ 当且仅当，即时等号成立．‎ 当时，，综上所述．‎ 当时，取得最大值，面积也取得最大值．‎ ‎.‎ ‎21.解：（1）令，有，当时，，当时，，所以在上单调递减，在上单调递增，在处取得最大值，为，若恒成立，则即.‎ ‎（2）由（1）可知，若函数 有两个零点，则，‎ 要证，只需证，由于在上单调递减，从而只需证，由，，‎ 即证 令，，‎ 有在上单调递增，，所以.‎ ‎22.由,得,‎ 化为直角坐标方程得,‎ 即曲线的直角坐标方程为.‎ 在直线的参数方程中,由,得,‎ 代入,可得,‎ 即直线的普通方程为.‎ 把代入曲线的直角坐标方程，‎ 得,‎ 整理得.‎ 设对应的参数分别为,则, ,显然.‎ 设,,‎ 则，‎ 所以.‎ ‎23.（Ⅰ）‎ 当时，由，解得；‎ 当时，不成立；‎ 当时，由，解得.‎ 所以不等式的解集为.‎ ‎（Ⅱ）因为，‎ 所以.‎ 由题意知对，，‎ 即，‎ 因为，‎ 所以，解得.‎