2018届二轮复习几何证明选讲课件（全国通用） 31页

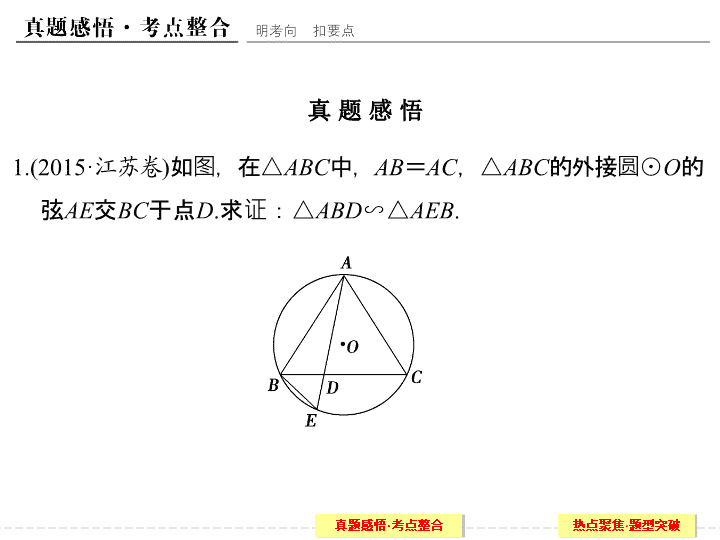
第 1 讲　几何证明选讲 高考定位 　 高考对本内容的考查主要有： (1) 三角形及相似三角形的判定与性质； (2) 圆的相交弦定理，切割线定理； (3) 圆内接四边形的性质与判定； (4) 相交弦定理，本内容考查属 B 级要求 . 真 题 感 悟 1. (2015· 江苏卷 ) 如图，在 △ ABC 中， AB ＝ AC ， △ ABC 的外接圆 ⊙ O 的弦 AE 交 BC 于点 D . 求证： △ ABD ∽△ AEB . 证明　 因为 AB ＝ AC ， 所以 ∠ ABD ＝ ∠ C . 又因为 ∠ C ＝ ∠ E ， 所以 ∠ ABD ＝ ∠ E ， 又 ∠ BAE 为公共角， 可知 △ ABD ∽△ AEB . 2. (2014· 江苏卷 ) 如图， AB 是圆 O 的直径， C ， D 是圆 O 上位于 AB 异侧的两点 . 证明： ∠ OCB ＝ ∠ D . 证明　 因为 B ， C 是圆 O 上的两点， 所以 OB ＝ OC . 故 ∠ OCB ＝ ∠ B . 又因为 C ， D 是圆 O 上位于 AB 异侧的两点， 故 ∠ B ， ∠ D 为同弧所对的两个圆周角， 所以 ∠ B ＝ ∠ D . 因此 ∠ OCB ＝ ∠ D . 考 点 整 合 1.(1) 相似三角形的判定定理 判定定理 1 ：对于任意两个三角形，如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似 . 判定定理 2 ：对于任意两个三角形，如果一个三角形的两边和另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似 . 判定定理 3 ：对于任意两个三角形，如果一个三角形的三条边和另一个三角形的三条边对应成比例，那么这两个三角形相似 . (2) 相似三角形的性质 ① 相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比； ② 相似三角形周长的比等于相似比； ③ 相似三角形面积的比等于相似比的平方 . (3) 直角三角形的射影定理：直角三角形中，每一条直角边是这条直角边在斜边上的射影与斜边的比例中项；斜边上的高是两直角边在斜边上射影的比例中项 . 2.(1) 圆周角定理：圆上一条弧所对的圆周角等于它所对的圆心角的一半 . (2) 圆心角定理：圆心角的度数等于它所对弧的度数 . 3.(1) 圆内接四边形的性质定理： ① 圆的内接四边形的对角互补； ② 圆内接四边形的外角等于它的内角的对角 . (2) 圆内接四边形判定定理：如果一个四边形的对角互补，那么这个四边形的四个顶点共圆 . 4.(1) 圆的切线的性质定理：圆的切线垂直于经过切点的半径 . (2) 圆的切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线 . (3) 弦切角定理：弦切角等于它所夹的弧所对的圆周角 . (4) 相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等 . (5) 切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项 . 5. 证明等积式成立，应先把它写成比例式，找出比例式中给出的线段所在三角形是否相似，若不相似 , 则进行线段替换或等比替换 . 6. 圆幂定理与圆周角、弦切角联合应用时，要注意找相等的角，找相似三角形，从而得出线段的比 . 由于圆幂定理涉及圆中线段的数量计算，所以应注意代数法在解题中的应用 . 热点一　三角形相似的判定及应用 [ 微题型 1] 　 利用弦切角定理证明三角形相似 证明： (1) ∠ ACE ＝ ∠ BCD ； (2) BC 2 ＝ BE · CD . 探究提高 　 在证明角或线段相等时，证三角形相似是首选的解题思路，如果涉及弦切角，则需考虑弦切角定理 . [ 微题型 2] 　 利用圆周角、圆心角定理证明三角形相似 【例 1 － 2 】 如图，已知圆 O 是 △ ABC 的外接圆， AB ＝ BC ， AD 是 BC 边上的高， AE 是圆 O 的直径，过点 C 作圆 O 的切线交 BA 的延长线于点 F . 探究提高 　 在证明线段的乘积相等时，通常用三角形相似或圆的切割线定理 . 同时，要注意等量的代换 . 【训练 1 】 已知 AB 为半圆 O 的直径， AB ＝ 4 ， C 为半圆上一点，过点 C 作半圆的切线 CD ，过点 A 作 AD ⊥ CD 于 D ，交半圆于点 E ， DE ＝ 1. (1) 求证： AC 平分 ∠ BAD ； (2) 求 BC 的长 . (1) 证明 　连接 OC ，因为 OA ＝ OC ，所以 ∠ OAC ＝ ∠ OCA . ∵ CD 为半圆的切线， ∴ OC ⊥ CD . ∵ AD ⊥ CD ， ∴ OC ∥ AD . ∴∠ OCA ＝ ∠ CAD ， ∴∠ OAC ＝ ∠ CAD ， ∴ AC 平分 ∠ BAD . (2) 解 　连接 CE ，由 (1) 得 ∠ OAC ＝ ∠ CAD ，由同圆或等圆中圆周角相等所对弧及弦也相等可知 BC ＝ CE . 热点二　四点共圆的判定及性质 [ 微题型 1] 　 四点共圆的判定 【例 2 － 1 】 如图，已知 △ ABC 的两条角平分线 AD 和 CE 相交于 H ， ∠ B ＝ 60° ， F 在 AC 上，且 AE ＝ AF . 证明： (1) B 、 D 、 H 、 E 四点共圆； (2) EC 平分 ∠ DEF . 证明　 (1) 在 △ ABC 中，因为 ∠ B ＝ 60° ，所以 ∠ BAC ＋ ∠ BCA ＝ 120°. 因为 AD 、 CE 是角平分线， 所以 ∠ HAC ＋ ∠ HCA ＝ 60° ， 故 ∠ AHC ＝ 120°. 于是 ∠ EHD ＝ ∠ AHC ＝ 120°. 因为 ∠ EBD ＋ ∠ EHD ＝ 180° ， 所以 B 、 D 、 H 、 E 四点共圆 . (2) 连接 BH ，则 BH 为 ∠ ABC 的平分线， 得 ∠ HBD ＝ 30°. 由 (1) 知 B 、 D 、 H 、 E 四点共圆， 所以 ∠ CED ＝ ∠ HBD ＝ 30°. 又 ∠ AHE ＝ ∠ EBD ＝ 60° ， 由已知可得 EF ⊥ AD ，可得 ∠ CEF ＝ 30°. 所以 EC 平分 ∠ DEF . 探究提高 　 (1) 如果四点与一定点距离相等，那么这四点共圆； (2) 如果四边形的一组对角互补，那么这个四边形的四个顶点共圆； (3) 如果四边形的一个外角等于它的内对角，那么这个四边形的四个顶点共圆 . [ 微题型 2] 　 考查四点共圆的性质 【例 2 － 2 】 如图所示，已知 AP 是 ⊙ O 的切线， P 为切点， AC 是 ⊙ O 的割线，与 ⊙ O 交于 B 、 C 两点，圆心 O 在 ∠ PAC 的内部，点 M 是 BC 的中点 . (1) 证明： A ， P ， O ， M 四点共圆； (2) 求 ∠ OAM ＋ ∠ APM 的大小 . (1) 证明　 连接 OP 、 OM ， ∵ AP 与 ⊙ O 相切于 P ， ∴ OP ⊥ AP ， 又 ∵ M 是 ⊙ O 的弦 BC 的中点， ∴ OM ⊥ BC ， 于是 ∠ OMA ＋ ∠ OPA ＝ 180° ， 由圆心 O 在 ∠ PAC 的内部， 可知四边形 APOM 的对角互补， ∴ A ， P ， O ， M 四点共圆 . (2) 解　 由 (1) 得 A ， P ， O ， M 四点共圆，可知 ∠ OAM ＝ ∠ OPM ，又 ∵ OP ⊥ AP ，由圆心在 ∠ PAC 的内部，可知 ∠ OPM ＋ ∠ APM ＝ 90° ， ∴∠ OAM ＋ ∠ APM ＝ 90°. 探究提高 　 利用四点共圆的性质可解决角的相等，或结合切割线定理解决线段成比例问题 . (1) 证明　 如图，设 F 为 AD 延长线上一点 . ∵ A 、 B 、 C 、 D 四点共圆， ∴∠ CDF ＝ ∠ ABC . 又 AB ＝ AC ， ∴∠ ABC ＝ ∠ ACB ， 且 ∠ ADB ＝ ∠ ACB ， ∴∠ ADB ＝ ∠ CDF .