2019届二轮复习对数函数及其性质课件（29张） 29页

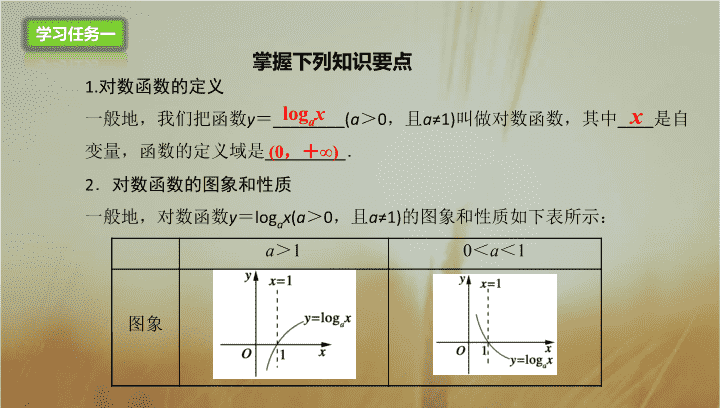
对数函数 及其 性质 学习目标 1 ． 理解对数函数的概念； 2 ． 掌握对数函数的图像与性质； 3 ． 了解对数函数在生产实际中的简单应用；加深对函数思想的理解． 4 ． 培养学生的数学交流能力和与人合作精神；用联系的观点分析问题，通过对对数函数的学习，渗透数形结合的数学思想． 学习任务一 掌握下列知识要点 1. 对数函数的定义 一般地，我们把函数 y ＝ ________( a ＞ 0 ，且 a ≠1) 叫做对数函数，其中 ____ 是自变量，函数的定义域是 _________ ． log a x x (0 ，＋ ∞) 2 ． 对数函数的图象和性质 一般地，对数函数 y ＝ log a x ( a ＞ 0 ，且 a ≠1) 的图象和性质如下表所示： 学习任务一 (0 ，＋ ∞) R (1,0) 增函数 减函数 学习任务二 完成 自主学习检测的 题目 D A A y ＝ log 3 x 情境导入 我们所处的地球正当壮年，地壳运动还非常频繁，每年用地震仪可以测出的地震大约有 500 万次，平均每隔几秒钟就有一次，其中 3 级以上的大约只有 5 万次，仅占 1%,7 级以上的大震每年平均约有 18 次， 8 级以上的地震每年平均仅 1 次，那么地震的震级是怎么定义的呢？这里面就要用到对数函数 . 新知讲解 1. 对数函数的定义 一般地，我们把函数 y ＝ ________( a ＞ 0 ，且 a ≠1) 叫做对数函数，其中 ____ 是自变量，函数的定义域是 _________ ． log a x x (0 ，＋ ∞) 合作探究 探究一： 对数函数概念 典例精析 例 1 、 题型一： 对数函数概念 [思路分析]　 (1)对数概念对底数、真数、系数的要求是什么？ [ 解析 ] 　 根据对数函数的定义进行判断．由于 ① 中自变量出现在底数上， ∴① 不是对数函数；由于 ② 中底数 a ∈ R 不能保证 a >0 且 a ≠1 ， ∴② 不是对数函数；由于 ⑤ 、 ⑦ 的真数分别为 ( x ＋ 2) ， ( x ＋ 1) ， ∴⑤ 、 ⑦ 也不是对数函数；由于 ⑥ 中 log 4 x 系数为 2 ， ∴⑥ 不是对数函数；只有 ③ 、 ④ 符合对数函数的定义． B 典例精析 [ 规律总结 ] 　对于对数概念要注意以下两点： (1) 在函数的定义中， a >0 且 a ≠1. (2) 在解析式 y ＝ log a x 中， log a x 的系数必须为 1 ，真数必须为 x ，底数 a 必须是大于 0 且不等于 1 的常数． 分组练习 A 组 B 组 【练习 2 】 【练习 1 】 我来 我来 我来 我来 小组展示 解析一览 合作探究 探究二： 对数函数的定义域 思考 1 ： 求函数的 定义域 时有哪些限制条件？ （ 1 ）分母不能为零，（ 2 ） 0 的零次幂与负指数次幂无意义， （ 3 ）偶次方根被开方式 ( 数 ) 非负 . 思考 2 ： 求对数函数的 定义域 时有哪些限制条件？ （ 1 ）一是要特别注意真数大于零；（ 2 ）二是要注意底数 a >0 且 a ≠1 ； 典例精析 例 2 、 题型二： 对数函数的定义域 典例精析 [ 规律总结 ] 　 若已知函数解析式求定义域，常规为分母不能为零， 0 的零次幂与负指数次幂无意义，偶次方根被开方式 ( 数 ) 非负，求与对数函数有关的函数定义域时，还要对这种函数自身有如下要求：一是要特别注意真数大于零；二是要注意底数；三是按底数的取值应用单调性． 分组练习 A 组 B 组 【练习 2 】 【练习 1 】 我来 我来 我来 我来 小组展示 解析一览 [ 答案 ] C [ 答案 ] C 　 (0 ，＋ ∞) R (1,0) 增函数 减函数 2 ． 对数函数的图象和性质 新知讲解 合作探究 探究三： 对数函数的图象 思考： 底数对对数函数图像的影响 典例精析 例 3 、 题型三： 对数函数的图象 [ 思路分析 ] 　 由图象来判断参数的大小情况，需要抓住图象的本质特征和关键点．根据图中的四条曲线底数不同及图象的位置关系，利用 log a a ＝ 1 ，结合图象判断． [解析] 　在图中作一条直线y＝1. 典例精析 [ 规律总结 ] 　 知函数 y ＝ log a x ( a ＞ 0 ，且 a ≠ 1) 的底数变化对图象位置的影响． (1) 上下比较：在直线 x ＝ 1 的右侧，当 a ＞ 1 时， a 越大，图象越靠近 x 轴； 当 0 ＜ a ＜ 1 时， a 越小，图象越靠近 x 轴． (2) 左右比较，在 x 轴上方，图象从左至右底数依次增大． 分组练习 A 组 B 组 【练习 2 】 我来 我来 我来 我来 小组展示 解析一览 [ 答案 ] 　 A 本课小结 对数函数及其性质 对数函数定义 图像与性质 随 堂检测 D C D 随 堂检测