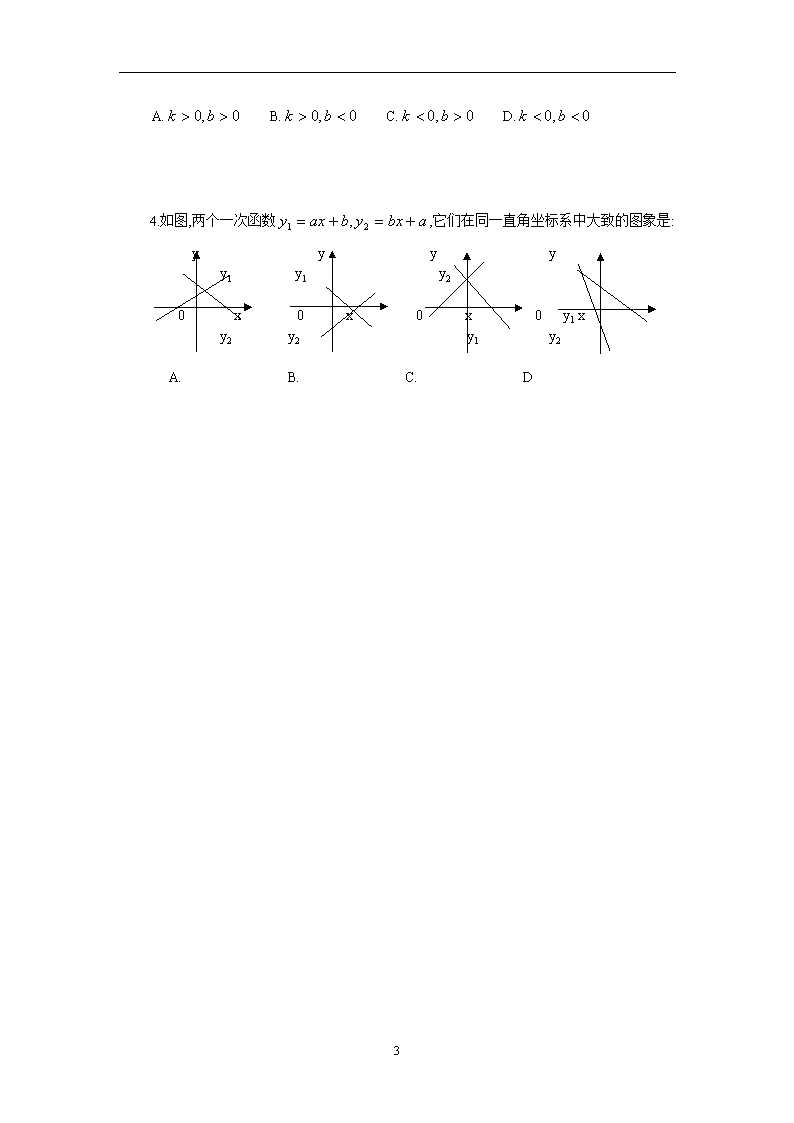一次函数的图象(2)教案 3页

‎ ‎ ‎5.3一次函数的图象(2)教案 教学目标 ‎1.理解一次函数及其图象的有关性质.‎ ‎2.能熟练地作出一次函数的图象.‎ ‎3.进一步培养学生数形结合的意识和能力.‎ 教学重点 一次函数的图象的性质.‎ 教学过程 ‎1.新课导入 上节课我们学习了如何画一次函数的图象，步骤为①列表；②描点；③连线.经过讨论我们又知道了画一次函数的图象不需要许多点，只要找两点即可，还明确了一次函数的代数表达式与图象之间的对应关系.‎ 本节课我们进一步来研究一次函数的图象的其他性质.‎ ‎2.讲授新课 ‎（1）首先我们来研究一次函数的特例——正比例函数有关性质.‎ 请大家在同一坐标系内作出正比例函数y=x，y=x，y=3x，y=-2x的图象.‎ 图：‎ ‎3.议一议 ‎（1）正比例函数y=kx的图象有什么特点？‎ ‎（2）你作正比例函数y=kx的图象时描了几个点？‎ ‎（3）直线y=x，y=x，y=3x中，哪一个与x轴正方向所成的锐角最大？哪一与x轴正方向所成的锐角最小？‎ ‎4.小结：正比例函数的图象有以下特点：‎ ‎（1）正比例函数的图象都经过坐标原点.‎ ‎（2）作正比例函数y=kx的图象时，除原点外，还需找一点，一般找（1,k）点.‎ ‎（3）在正比例函数y=kx图象中，当k>0时，k的值越大，函数图象与x轴正方向所成的锐角越大.‎ ‎（4）在正比例函数y=kx的图象中，当k>0时，y的值随x值的增大而增大；当k<0时，y的值随x值的增大而减小.‎ ‎5.做一做 3‎ ‎ ‎ 在同一直角坐标系内作出一次函数y=2x+6,y=-x,y=-x+6,y=5x的图象.‎ 一次函数y=kx+b的图象的特点：分析：在函数y=2x+6中，k>0，y的值随x值的增大而增大；在函数y=-x+6中，y的值随x值的增大而减小.‎ 由上可知，一次函数y=kx+b中，y的值随x的变化而变化的情况跟正比例函数的图象的性质相同.‎ 对照正比例函数图象的性质，可知一次函数的图象不过原点，但是和两个坐标轴相交.在作一次函数的图象时，也需要描两个点.一般选取（0，b），（-，0）比较简单.‎ ‎6.想一想 ‎（1）x从0开始逐渐增大时，y=2x+6和y=5x哪一个值先达到20？这说明了什么？‎ ‎（2）直线y=-x与y=-x+6的位置关系如何？‎ ‎（3）直线y=2x+6与y=-x+6的位置关系如何？‎ ‎ 7.在同一直角坐标系内作出一次函数y=2x,y=2x+3, y=2x-3的图象.探索一次函数y=kx+b中, b的值对一次函数图象的影响.‎ 总结：‎ 1、 正比例函数y=kx的图象的特点.‎ 2、 一次函数y=kx+b的图象的特点.‎ ‎3.一次函数y=kx+b的k、b的值对一次函数图象的影响. y ‎①的图象在一、二、三象限 0 x ‎ y ‎②的图象在一、三、四象限 0 x ‎ y ‎③图象在一、二、四象限 0 x ‎ y ‎④图象在二、三、四象限 0 x ‎ 补充练习：‎ ‎1.下列一次函数中，y的值随x值的增大而增大的是（ ）‎ A.y=-5x+3 B.y=-x-7 C.y=- D.y=-+4‎ ‎2、下列一次函数中，y的值随x值的增大而减小的是（ ）‎ A.y=x-8 B.y=-x+3 C.y=2x+5 D.y=7x-6‎ ‎3、若一次函数的图象经过一、二、三象限,则应满足的条件是:‎ 3‎ ‎ ‎ A. B. C. D.‎ ‎4.如图,两个一次函数,它们在同一直角坐标系中大致的图象是:‎ ‎ y y y y ‎ y1 y1 y2‎ ‎ ‎ ‎ 0 x 0 x 0 x 0 y1 x ‎ y2 y2 y1 y2‎ ‎ A. B. C. D 3‎