中考数学模拟复习试卷 12页

石景山区2012年初三第二次统一练习 数 学 试 卷 考 生 须 知 ‎1．本试卷共10页．第10页为草稿纸，全卷共五道大题，25道小题．‎ ‎2．本试卷满分120分，考试时间120分钟．‎ ‎3．在试卷密封线内准确填写区（县）名称、毕业学校、姓名和准考证号．‎ ‎4．考试结束后，将试卷和答题纸一并交回．‎ ‎ ‎ 第Ⅰ卷（共32分）‎ 一、选择题（本题共32分，每小题4分）‎ ‎ 在每个小题给出的四个备选答案中，只有一个是正确的，请将所选答案前的字母填在题后的括号内．‎ ‎1．的算术平方根是（ ）‎ A． B． C． D． ‎ ‎2．2012年2月，国务院同意发布新修订的《环境空气质量标准》增加了PM2.5监测指标．PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物．如果1微米=0．000 001 米，那么数据0.000 002 5用科学记数法可以表示为（ ）‎ A． B． C． D．‎ ‎3．如图，把一个长方形的纸片对折两次，然后剪下一个角，为了得到一个钝角为120° 的菱形，剪口与折痕所成的角a 的度数应为（ ）‎ 第3题图 A．15°或30° B．30°或45° C．45°或60° D．30°或60° ‎4．北京市2001-2010年星级饭店客房出租率（%）的情况如下表：‎ 年份 ‎2001‎ ‎2002‎ ‎2003‎ ‎2004‎ ‎2005‎ ‎2006‎ ‎2007‎ ‎2008‎ ‎2009‎ ‎2010‎ 出租率 ‎62‎ ‎62‎ ‎52‎ ‎65‎ ‎62‎ ‎61‎ ‎60‎ ‎52‎ ‎49‎ ‎56‎ 表中出租率（%）的中位数和众数分别为（ ）‎ A．61、62 B．62、62 C．61.5、62 D．60.5、62‎ ‎5．如图，有6张形状、大小、质地均相同的卡片，正面分别印有北京精神——“爱国、创新、包容、厚德”的字样．背面完全相同，现将这6张卡片洗匀后正面向下放在桌子上，从中随机抽取一张，抽出的卡片恰好是“创新”的概率是（ ） ‎ 爱国 创新爱国 包容爱国 厚德爱国 爱国 创新爱国 ‎ A． B． C． D．‎ ‎6．若一个多边形的内角和是900°，则这个多边形的边数是（ ） ‎ A．5 B．6 C．7 D．8‎ ‎7．将二次函数的图象如何平移可得到的图象（ ）‎ A．向右平移2个单位，向上平移一个单位 ‎ B．向右平移2个单位，向下平移一个单位 ‎ C．向左平移2个单位，向下平移一个单位 D．向左平移2个单位，向上平移一个单位 ‎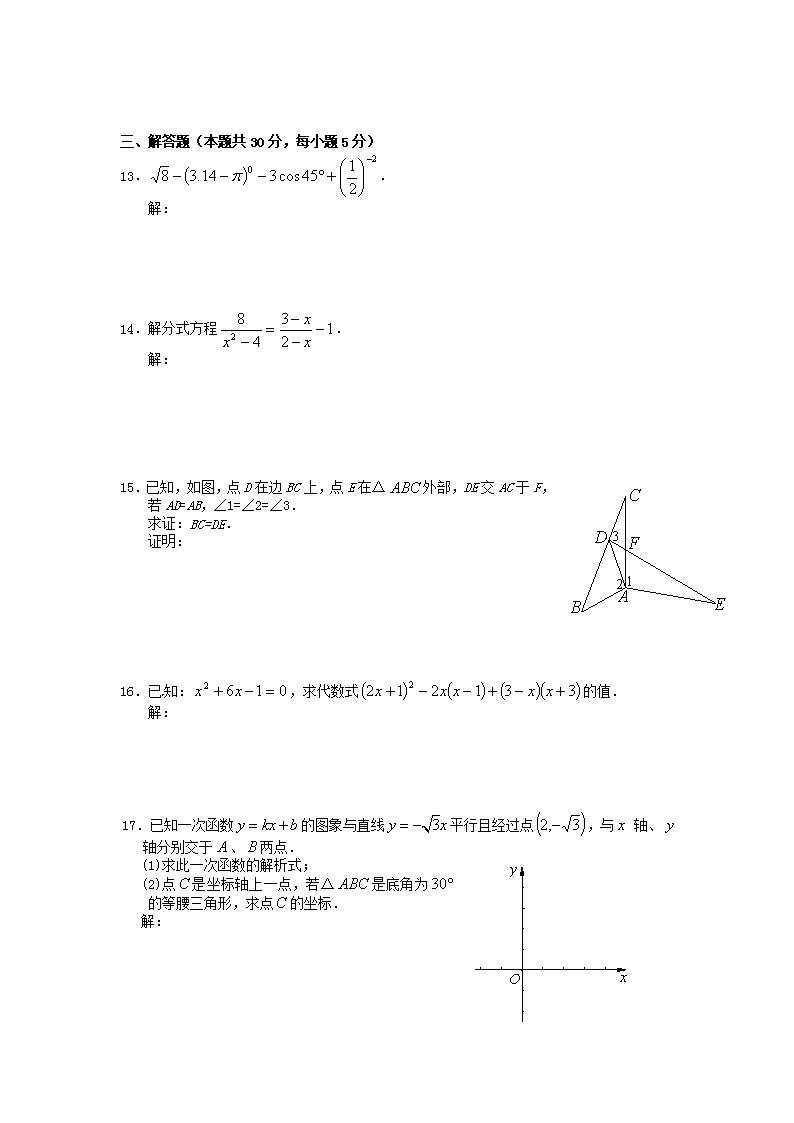8．已知正方形纸片的边长为18，若将它按下图所示方法折成一个正方体纸盒，则纸盒的边（棱）长是（ ）‎ ‎ A． B． C． D．‎ 第8题图 ‎ ‎ 第Ⅱ卷（共88分）‎ 二、填空题（本题共16分，每小题4分）‎ ‎9．分式有意义的条件为 ．‎ 第11题图 ‎10．分解因式：______ ________．‎ ‎11．已知：如图是斜边为10的一个等腰直角三角形与两个半径为5的扇形的重叠情形，其中等腰直角三角形顶角平分线与两扇形相切，则图中阴影部分面积的和是 ．‎ 第12题图 ‎12．如图所示，圆圈内分别标有1，2，…，12，这12个数字，电子跳蚤每跳一步，可以从一个圆圈逆时针跳到相邻的圆圈，若电子跳蚤所在圆圈的数字为，则电子跳蚤连续跳（）步作为一次跳跃，例如：电子跳蚤从标有数字1的圆圈需跳步到标有数字2的圆圈内，完成一次跳跃，第二次则要连续跳步到达标有数字6的圆圈，…依此规律，若电子跳蚤从①开始，那么第3次能跳到的圆圈内所标的数字为 ；第2012次电子跳蚤能跳到的圆圈内所标的数字为 ．‎ 三、解答题（本题共30分，每小题5分）‎ ‎13．．‎ 解：‎ ‎ ‎ ‎14．解分式方程．‎ 解：‎ ‎15．已知，如图，点D在边BC上，点E在△外部，DE交AC于F，若AD=AB，∠1=∠2=∠3．‎ 求证：BC=DE．‎ 证明：‎ ‎16．已知：，求代数式的值． ‎ 解：‎ ‎17．已知一次函数的图象与直线平行且经过点，与 轴、轴分别交于、两点．‎ ‎(1)求此一次函数的解析式；‎ ‎(2)点是坐标轴上一点，若△是底角为的等腰三角形，求点的坐标．‎ 解：‎ ‎18．列方程（组）解应用题：‎ 如图是一块长、宽分别为60 m、50 m的矩形草坪，草坪中有宽度均为x m的一横两纵的甬道．‎ ‎（1）用含x的代数式表示草坪的总面积S ；‎ ‎（2）当甬道总面积为矩形总面积的%时，求甬道的宽．‎ 解：‎ 四、解答题（本题共20分，每小题5分）‎ ‎19．如图，梯形纸片ABCD中，AD//BC，∠B=30º．折叠纸片使BC经过点A，点B落在点B’处，EF是折痕，且BE=EF=4，∥．‎ ‎（1）求∠BAF的度数；‎ ‎（2）当梯形的上底多长时，线段恰为该梯形的高？‎ 解：‎ ‎2011年各类粮食占全体 粮食的百分比分组统计图 ‎20．以下是根据全国 2011年国民经济和社会发展统计公报中的相关数据，绘制的统计图的一部分．‎ 请根据以上信息，解答下列问题：（产量相关数据精确到1万吨）‎ ‎（1）请补全扇形统计图；‎ ‎（2）通过计算说明全国的粮食产量与上一年相比，增长最多的是 年；‎ ‎（3）2011年早稻的产量为 万吨；‎ ‎（4）2008-2011‎ 这三年间，比上一年增长的粮食产量的平均数为多少万吨，若按此平均数增长，请你估计2012年的粮食产量为多少万吨．（结果保留到整数位）‎ 解：‎ ‎21．已知：如图，是⊙的直径上任意一点，过点作的垂线，是的延长线上一点，联结交⊙于点，且．‎ ‎（1）判断直线与⊙的位置关系，并证明你的结论；‎ ‎（2）若，，过点A作的平行线交⊙于点．求弦的长．‎ 解：‎ 新课 标第 一网 ‎22．阅读下面材料：‎ ‎ 小阳遇到这样一个问题：如图（1），O为等边△内部一点，且，求的度数.‎ 图⑴ 图⑵ 图⑶‎ 小阳是这样思考的：图（1）中有一个等边三角形，若将图形中一部分绕着等边三角形的某个顶点旋转60°，会得到新的等边三角形，且能达到转移线段的目的.他的作法是：如图（2），把△绕点A逆时针旋转60°，使点C与点B重合，得到△，连结. 则△是等边三角形，故，至此，通过旋转将线段OA、OB、OC转移到同一个三角形中.‎ ‎（1）请你回答：.‎ ‎（2）参考小阳思考问题的方法，解决下列问题：‎ 已知：如图（3），四边形ABCD中，AB=AD，∠DAB=60°，∠DCB=30°，AC=5，CD=4.求四边形ABCD的面积.‎ 解：‎ 图（3）‎ 五、解答题（本题满分22分,第23题7分，第24题7分，第25题8分）‎ ‎23．已知：直线分别与 x轴、y轴交于点A、点B，点P（，b）在直线AB 上，点P关于轴的对称点P′ 在反比例函数图象上．‎ ‎(1) 当a=1时，求反比例函数的解析式；‎ ‎(2) 设直线AB与线段P'O的交点为C．当P'C =2CO时，求b的值；‎ ‎(3) 过点A作AD//y轴交反比例函数图象于点D，若AD=，求△P’DO的面积． ‎ 解：‎ 备用图 ‎24．在△中，,是底边上一点，是线段上一点,且 ‎∠．‎ ‎(1) 如图1,若∠,猜想与的数量关系为 ；‎ ‎(2) 如图2,若∠，猜想与的数量关系，并证明你的结论；‎ 图1 图2‎ ‎（3）若∠，请直接写出与的数量关系.‎ 解：‎ ‎25．已知：抛物线y＝－x2＋2x＋m-2交y轴于点A（0，2m-7）．与直线 y＝x交于点B、C（B在右、C在左）．‎ ‎（1）求抛物线的解析式； ‎ ‎（2）设抛物线的顶点为E，在抛物线的对称轴上是否存在一点F，使得，若存在，求出点F的坐标，若不存在，说明理由；‎ ‎（3）射线OC上有两个动点P、Q同时从原点出发，分别以每秒个单位长度、每秒2个单位长度的速度沿射线OC运动，以PQ为斜边在直线BC的上方作直角三角形PMQ（直角边分别平行于坐标轴），设运动时间为t秒，若△PMQ与抛物线y＝－x2＋2x＋m-2有公共点，求t的取值范围．‎ 解：‎ Xk b1 .c om 备用图 石景山区2012初三第二次统一练习 数学参考答案 阅卷须知：‎ ‎1．一律用红钢笔或红圆珠笔批阅．‎ ‎2．为了阅卷方便，解答题中的推导步骤写得较为详细，考生只要写明主要过程即可．若考生的解法与本解法不同，正确者可参照评分参考给分，解答右端所注分数，表示考生正确做到这一步应得的累加分数．‎ 一、选择题（本题共8道小题，每小题4分，共32分）‎ 题 号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答 案 Ｂ A D D A C ‎ C Ｂ 二、填空题（本题共4道小题，每小题4分，共16分）‎ ‎9．； 10．； 11．； 12．10；6．‎ 三、解答题（本题共6道小题，每小题5分，共30分）‎ ‎13．解：‎ ‎ = ……………………………4分 ‎ =…………………………………………………5分 ‎14． ‎ 解： ……………………………1分 ‎ ……………………………3分 ‎ ……………………………4分 ‎∴ ‎ 经检验：是原方程的根．………………………5分 ‎15．证明：∵∠1=∠2=∠3‎ ‎∴…………………………… 1分 又∵‎ ‎∴ …………………………… 2分 在△和△中 ‎…………………………… 3分 ‎∴△≌△ ……………………………………………………… 4分 ‎∴BC=DE． ……………………………………………………… 5分 ‎16．解：原式 …………………………………2分 ‎ ………………………………… 3分 ‎ 当时， ………………………………… 4分 原式． …………………………………5分 ‎17．解：(1)∵一次函数的图象与直线平行且经过点 ‎∴ 解得 ‎∴一次函数解析式为 …………………………………1分 ‎(2)令，则；令则 ‎∴‎ ‎∵, …………………………2分 ‎∴ ‎ ‎∴‎ 若，可求得点的坐标为或………………………4分 若新课 标第 一网 如图，‎ ‎∴ …………………………………………5分 ‎∴,,‎ ‎ 18．解：（1）S = －（60 x + 2×50 x－2×x2 ）=3000 + 2x2 －160x．………2分 ‎（2）由题意得：-2x2+160x =， ………………3分 解得 x = 2 或 x = 78． …………………………………4分 又0＜x＜50，所以x = 2，‎ 答：甬道的宽是2米． ……………………………………5分 ‎19. 解：（1）∵BE=EF∴∠EFB=∠B，由题意，△≌△‎ ‎∴∠EFB’ =∠EFB=∠B=30°‎ ‎∴△中， ……………………………………2分 ‎（2）联结DF，‎ ‎∵AD//BC，∥‎ ‎∴四边形是平行四边形 ……………………………………3分 ‎∴∠C =∠AFB=60°‎ ‎∴== ……………………………………4分 若，则 此时． ……………………………………5分 ‎20．（1）72%；（2）2011；（3）3427； ……………………每空1分，共3分 ‎（4）（57121-52871）÷3≈=1417 ………………………………………4分 ‎57121+1417=58538. ………………………………………5分 ‎21.（1）联结CO, … …………………………………1分 ‎∵DM⊥AB ‎∴∠D+∠A=90°‎ ‎∵‎ ‎∴∠D=∠PCD ‎∵OC=OA ‎∴∠A=∠OCA ‎∴∠OCA+∠PCD=90°‎ ‎∴PC⊥OC ‎∴直线是⊙的切线 …………………………………2分 ‎（2）过点A作的平行线交⊙于点．‎ ‎∴∠NAC=∠PCD=∠D, AN⊥OC,设垂足是Q ‎∴Rt△中 ‎∴‎ ‎∴设CQ=x，AQ= ww w.xkb 1.com ‎ ‎∴OQ=‎ ‎∵‎ ‎∴‎ 解得 …………………………………4分 ‎∴‎ ‎∴ …………………………………5分 ‎22. 解：（1）150° ………………………1分 ‎(2) 如图，将△绕点顺时针旋转60°，使点D与点B重合，………2分 得到△，连结. 则△是等边三角形，‎ 可知， ……………………3分 在四边形ABCD中，,‎ ‎ ‎ ‎． ……………………4分 ‎ ‎ ‎．………………5分 ‎23．（1）∵点在直线上, 时，‎ ‎=………………………1分 ‎∴， ‎ ‎∴，代入 得， ‎ ‎∴ …………………………2分 ‎（2）联结 ‎∵点和点关于轴对称 ‎∴∥轴 ‎∴‎ ‎∴∶∶ …………3分 ‎∵ ∴=‎ ‎∵与轴交于点、点 ‎∴，可得 ‎∴ ∴=4 ‎ ‎∴ ………………………5分 ‎（3）当点在第一象限时：‎ ‎∵点和点关于轴对称且 ‎∴‎ ‎∵∴‎ ‎∵在上 ‎∴ ‎ ‎∴‎ ‎∴‎ ‎∵‎ ‎∴ …………6分 当点在第二象限时：‎ ‎∴ ‎ ‎∴‎ ‎∴‎ ‎∵‎ ‎∴ …………7分 ‎24.解：（1）‎ ‎(2) ‎ 证明：过点作∥交的延长线于点,‎ 图(1)‎ 在 上取点使得 ‎∴‎ ‎∵‎ ‎∴,‎ ‎∴‎ ‎∵‎ ‎∴‎ ‎∵‎ ‎∴△≌△‎ 图(2)‎ ‎∴‎ ‎∵‎ ‎∴‎ ‎∴‎ 由△∽△得 ‎∴‎ ‎(3) 结论：.‎ ‎25.解：（1）点A（0，2m-7）代入y＝－x2＋2x＋m-2，得m=5‎ ‎∴抛物线的解析式为y＝－x2＋2x＋3 ………………………2分 ‎（2）由得，‎ ‎∴B（），C（）‎ B（）关于抛物线对称轴的 对称点为 可得直线的解析式为，‎ 由，可得 ‎∴ ………………………5分 ‎（3）当在抛物线上时，可得，，‎ 当在抛物线上时，可得，，‎ 舍去负值，所以t的取值范围是．………………8分