【数学】2018届一轮复习人教A版正弦定理、余弦定理教案 11页

‎　‎ 掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题．‎ 知识点一 正弦定理和余弦定理 ‎ 定理 正弦定理 余弦定理 内容 ‎________________＝2R a2＝______________‎ b2＝______________‎ c2＝______________‎ 变形 形式 ‎①a＝______，b＝______，‎ c＝________‎ ‎②sinA＝____，sinB＝____，‎ sinC＝______‎ ‎(其中R是△ABC外接圆半径)‎ ‎③abc＝______________‎ ‎④asinB＝bsinA，bsinC＝csinB，asinC＝csinA cosA＝________；‎ cosB＝________；‎ cosC＝________‎ 解决 解斜 三角 形的 ‎①已知两角和任一边，求另一角和其他两条边；‎ ‎②已知两边和其中一边的对角，求另一边和其他两角 ‎①已知三边，求各角；‎ ‎②已知两边和它们的夹角，求第三边和其他两个角 问题 答案 ＝＝　b2＋c2－2bccosA　a2＋c2－2accosB a2＋b2－2abcosC　2RsinA　2RsinB　2RsinC　　　　sinAsinBsinC　　　 ‎1．(2016·天津卷)在△ABC中，若AB＝，BC＝3，∠C＝120°，则AC＝(　　)‎ A．1 B．2‎ C．3 D．4‎ 解析：设△ABC中，角A，B，C的对边分别为a，b，c，则a＝3，c＝，∠C＝120°，由余弦定理得13＝9＋b2＋3b，解得b＝1，即AC＝1.‎ 答案：A ‎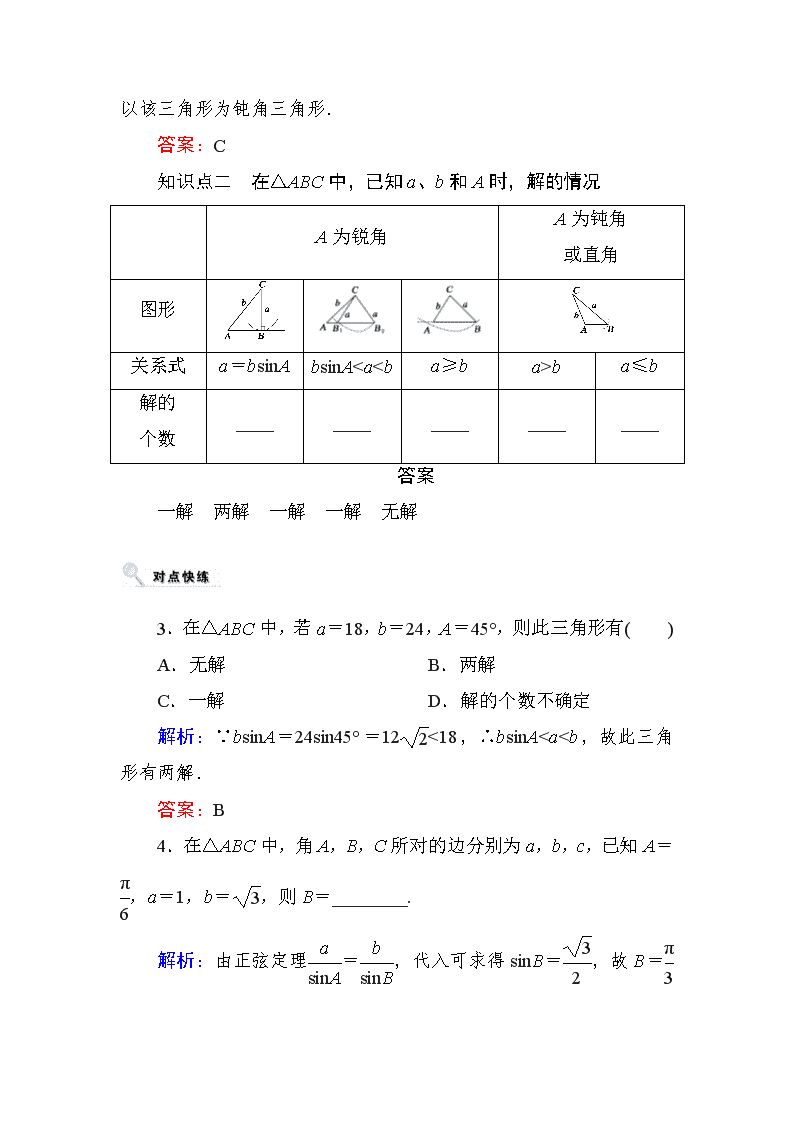2．(必修⑤P10习题1.1B组第2题改编)在△ABC中，若sin‎2A＋sin2Bb a≤b 解的 个数 ‎____‎ ‎____‎ ‎____‎ ‎____‎ ‎____‎ 答案 一解　两解　一解　一解　无解 ‎3．在△ABC中，若a＝18，b＝24，A＝45°，则此三角形有(　　)‎ A．无解 B．两解 C．一解 D．解的个数不确定 解析：∵bsinA＝24sin45°＝12<18，∴bsinA