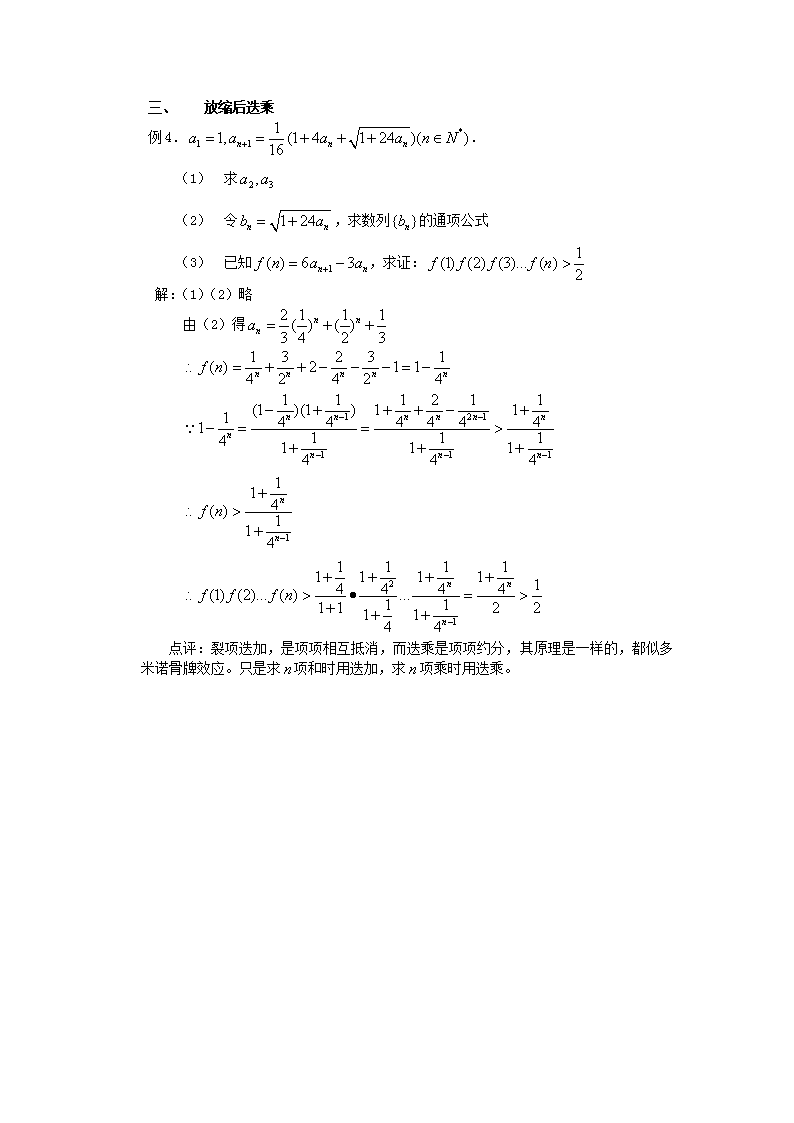- 182.50 KB
- 2021-05-13 发布
放缩法在数列不等式证明中的运用
高考中利用放缩方法证明不等式,文科涉及较少,但理科却常常出现,且多是在压轴题中出现。放缩法证明不等式有法可依,但具体到题,又常常没有定法,它综合性强,形式复杂,运算要求高,往往能考查考生思维的严密性,深刻性以及提取和处理信息的能力,较好地体现高考的甄别功能。本文旨在归纳几种常见的放缩法证明不等式的方法,以冀起到举一反三,抛砖引玉的作用。
一、 放缩后转化为等比数列。
例1. 满足:
(1) 用数学归纳法证明:
(2) ,求证:
解:(1)略
(2)
又
,
迭乘得:
点评:把握“”这一特征对“”进行变形,然后去掉一个正项,这是不等式证明放缩的常用手法。这道题如果放缩后裂项或者用数学归纳法,似乎是不可能的,为什么?值得体味!
二、放缩后裂项迭加
例2.数列,,其前项和为
求证:
解:
令,的前项和为
当时,
点评:本题是放缩后迭加。放缩的方法是加上或减去一个常数,也是常用的放缩手法。值得注意的是若从第二项开始放大,得不到证题结论,前三项不变,从第四项开始放大,命题才得证,这就需要尝试和创新的精神。
例3.已知函数的图象在处的切线方程为
(1)用表示出
(2)若在上恒成立,求的取值范围
(3)证明:
解:(1)(2)略
(3)由(II)知:当
令
且当
令
即
将上述n个不等式依次相加得
整理得
点评:本题是2010湖北高考理科第21题。近年,以函数为背景建立一个不等关系,然后对变量进行代换、变形,形成裂项迭加的样式,证明不等式,这是一种趋势,应特别关注。当然,此题还可考虑用数学归纳法,但仍需用第二问的结论。
三、 放缩后迭乘
例4..
(1) 求
(2) 令,求数列的通项公式
(3) 已知,求证:
解:(1)(2)略
由(2)得
点评:裂项迭加,是项项相互抵消,而迭乘是项项约分,其原理是一样的,都似多米诺骨牌效应。只是求项和时用迭加,求项乘时用迭乘。
相关文档
- 2019版高考语文一轮复习第二部分古2021-05-13 02:25:207页
- 人教新课标小学二年级上册数学第52021-05-13 02:25:204页
- 广东高考广东历史卷试题评析2021-05-13 02:25:104页
- 【数学】黑龙江省哈尔滨师范大学青2021-05-13 02:25:019页
- 二年级下册数学教案 3对称 北京版 2021-05-13 02:24:524页
- 2019高考语文第一轮总复习提分卡分2021-05-13 02:24:5217页
- 苏教版六年级下册数学教案设计-第22021-05-13 02:24:413页
- 甘肃省天水市第一中学2019-2020学2021-05-13 02:23:3913页
- 【物理】四川省广元市2020届高三上2021-05-13 02:23:2917页
- 2013高考英语一轮复习方略 素能提2021-05-13 02:23:117页