- 1.37 MB
- 2021-05-12 发布
2019-2020学年度会宁一中高一第一次数学月考卷
一、单项选择
1.下列语句正确的是( )
A. B. C. D.
【答案】B
【解析】
【详解】赋值语句的表示形式为:变量=表达式(其中“=”为赋值号),故A错误;
输入语句INPUT 中,命令动词INPUT 后面应写成“s=”,1,故C错误;
输出语句PRINT ,命令动词PRINT后面应写成“”,2,故D错误;
故选B
2.一个容量为80的样本中数据的最大值是140,最小值是51,组距是10,则应将样本数据分为( )
A. 10组 B. 9组 C. 8组 D. 7组
【答案】B
【解析】
由题意知,,所以分为组较为恰当,故选B.
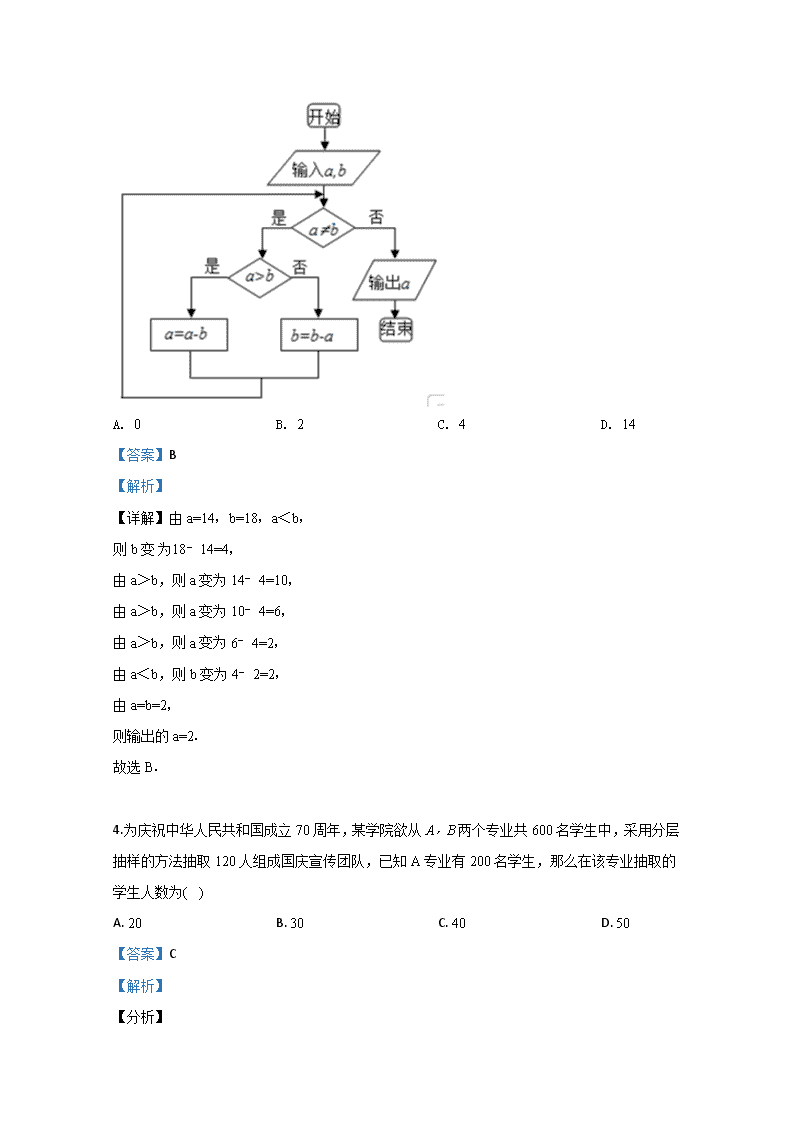
3.右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入分别为14,18,则输出的( )
A. 0 B. 2 C. 4 D. 14
【答案】B
【解析】
【详解】由a=14,b=18,a<b,
则b变18﹣14=4,
由a>b,则a变为14﹣4=10,
由a>b,则a变为10﹣4=6,
由a>b,则a变为6﹣4=2,
由a<b,则b变为4﹣2=2,
由a=b=2,
则输出的a=2.
故选B.
4.为庆祝中华人民共和国成立70周年,某学院欲从A,B两个专业共600名学生中,采用分层抽样的方法抽取120人组成国庆宣传团队,已知A专业有200名学生,那么在该专业抽取的学生人数为( )
A. 20 B. 30 C. 40 D. 50
【答案】C
【解析】
【分析】
先计算出抽样比,然后根据(A专业人数)乘以(抽样比)即可得到应抽取的人数.
【详解】据题意可知:抽样比为,则A专业抽取人数为人,
故选C.
【点睛】本题考查分层抽样的应用,难度较易.若要计算分层抽样的每一层应抽取数量,先要计算抽样比,利用每一层数量乘以抽样比得到该层应抽取的数量.
5.执行如图所示的程序框图,则输出的的值为( )
A. 9 B. 7 C. 5 D. 3
【答案】A
【解析】
【分析】
依次代入循环结构,得到正确结果.
【详解】第一次循环: ;
第二次循环: ;
第三次循环:;
第四次循环:,此时输出 .
【点睛】本题考查了程序框图的循环结构,这类题型在退出循环结构,计算结果时,注意是当型还是直到型,条件是不同的.
6.一个频率分布表(样本容量为)不小心被损坏了一部分,只记得样本中数据在上的频率为,则估计样本在、内的数据个数共有( )
A. B. C. D.
【答案】B
【解析】
【分析】
计算出样本在的数据个数,再减去样本在的数据个数即可得出结果.
【详解】由题意可知,样本在的数据个数为,
样本在的数据个数为,
因此,样本在、内的数据个数为.
故选:B.
【点睛】本题考查利用频数分布表计算频数,要理解频数、样本容量与频率三者之间的关系,考查计算能力,属于基础题.
7.设分别是先后抛掷一枚骰子得到的点数,则方程有实根的概率为( )
A. B. C. D.
【答案】A
【解析】
由题意知本题是一个等可能事件的概率,
试验发生包含的事件数是6×6=36种结果,
方程x2+mx+n=0有实根要满足m2−4n⩾0,
当m=2,n=1
m=3,n=1,2
m=4,n=1,2,3,4
m=5,n=1,2,3,4,5,6,
m=6,n=1,2,3,4,5,6
综上可知共有1+2+4+6+6=19种结果
∴方程x2+mx+n=0有实根的概率是;
本题选择A选项.
8.如图所示,5组数据中去掉后,下列说法正确的是( )
A. 偏差平方和变大 B. 相关系数变小
C. 负相关变为正相关 D. 解释变量与预报变量的相关性变强
【答案】D
【解析】
【分析】
由散点图知,去掉后,与的线性相关加强,由相关系数,相关指数及残差平方和与相关性的关系得出选项.
【详解】解:由散点图知,去掉后,与的线性相关加强,且为正相关,
所以变大,变大,偏差平方和变小.
故选:D.
【点睛】本题考查刻画两个变量相关性强弱的量:相关系数,相关指数及残差平方和,属于基础题.
9.从中任取一个数x,从中任取一个数y,则使的概率为( )
A. B. C. D.
【答案】D
【解析】
【分析】
在平面直角坐标系中作出图形,则x∈[0,2],y∈[0,3]的平面区域为矩形,符合条件x2+y2≤4的区域为以原点为圆心,2为半径的扇形内部,则扇形面积与矩形面积的比为概率
【详解】在平面直角坐标系中作出图形,如图所示,
则x∈[0,2],y∈[0,3]的平面区域为矩形OABC,
符合条件x2+y2≤4的区域为以原点为圆心,
2为半径的扇形OAD内部,
∴P(x2+y2≤4);
故选D.
【点睛】本题考查了几何概型的概率计算,正确作出几何图形是解题的关键.
10.秦九韶算法是中国南宋时期的数学家秦九韶提岀的一种多项式简化算法.秦九韶算法是一种将一元n次多项式的求值问题转化为n个一次式的算法.其大大简化了计算过程,即便在现代,利用计算机解决多项式的求值问題时,秦九韶算法依然是最优的算法.用秦九韶算法计算当时函数的值时,需要进行加法运算的次数及函数值分别为( )
A. 3,5.6426 B. 4,5.6426 C. 3,5.6416 D. 4,5.6416
【答案】C
【解析】
【分析】
根据秦九韶算法的原理,将变形,然后计算出加法次数和函数值.
【详解】因为
,
所以加法运算次数为:,且,
故选C.
【点睛】本题考查利用秦九韶算法计算加法运算次数以及函数值,难度较易.
11.某统计部门对四组数据进行统计分析后,获得如图所示的散点图,关于相关系数的比较,其中正确的是( )
A. B.
C. D.
【答案】C
【解析】
【分析】
根据相关系数的特点,可知(1)(3)为正相关,(2)(4)为负相关,再由相关性的强弱可比较出大小关系.
【详解】根据散点图的特征,数据大致呈增长趋势的是正相关,数据呈递减趋势的是负相关;数据越集中在一条线附近,说明相关性越强,
由题中数据可知:(1)(3)为正相关,(2)(4)为负相关;
故,;,;
又(1)与(2)中散点图更接近于一条直线,故,,
因此,.
故选C.
【点睛】相关系数:
当r>0时,表明两个变量正相关;当r<0时,表明两个变量负相关;
r的绝对值越接近于1,表明两个变量的线性相关性越强,r的绝对值越接近于0时,表明两个变量之间几乎不存在线性相关关系.
12.计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制数的对应关系如下表:
十六进制
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
十进制
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
例如,用十六进制表示:E+D=1B,则C×D等于( )
A. 5F B. 72 C. 6E D. 9C
【答案】D
【解析】
【分析】
在表中找出C、D对应的十进制数字,然后求出C×D,再根据表中C对应的十进制数字可把C×D用十六进制表示.
【详解】由表格知,C对应的十进制数为12,D对应的十进制数为13,
所以
由十进制表示为:
又表格中C对应的十进制为12,所以用十六进制表示为:C×D=9C
故选D
【点睛】本题考查了十进制与十六进制数的转化,属于较为基础题.
二、填空题
13.在区间[﹣2,4]上随机地取一个数x,若x满足|x|≤m的概率为,则m= _________ .
【答案】3
【解析】
【详解】如图区间长度是6,区间[﹣2,4]上随机地取一个数x,若x满足|x|≤m的概率为,若m对于3概率大于,若m小于3,概率小于,所以m=3.
故答案为3.
14.下表为某公司员工连续加班时间与制造产品的几组数据,根据表中提供的数据,求出关于的线性回归方程为,则表中的值为______.
3
4
5
6
2.5
t
4
4.5
【答案】3
【解析】
【分析】
根据线性回归方程过样本中心点,可代入得,再计算即可.
【详解】,∴,∴,∴
故答案为:3
【点睛】本题主要考查了线性回归方程经过样本中心点的问题,属于基础题.
15.一个算法的程序框图如下图所示,若该程序输出的结果为,则判断框中应填入的条件是____.
【答案】
【解析】
试题分析:由于,第一次执行循环体之后,,条件成立,第二次执行循环体之后,
,条件成立,第三次执行循环体之后,,条件成立,第四次执行循环体之后,
,条件成立,第五次执行循环体之后,,条件不成立,退出循环,输出结果,
故判断框的条件.
考点:程序框图的应用.
16.下列结论:①函数关系是一种确定性关系;②相关关系是一种非确定性关系;③回归分析是对具有函数关系的两个变量进行统计分析的一种方法;④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.其中正确的是______.(将所有正确的序号填上)
【答案】①②④
【解析】
【分析】
根据函数关系、相关关系与回归分析的定义辨析即可.
【详解】根据函数关系及相关关系的定义,①函数关系是一种确定性关系.②相关关系是一种非确定性关系.是正确的;由回归分析的定义及应用可知,④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.
故答案为:①②④.
【点睛】本题主要考查了回归分析的辨析,属于基础题.
三、解答题
17.(1)用辗转相除法求840与1764的最大公约数.
(2)用秦九韶算法计算函数时的函数值.
【答案】(1)84;(2)62.
【解析】
【分析】
(1)直接用辗转相除法计算;
(2)按秦九韶算法计算.
【详解】(1)1764÷840=2余84,
840÷84=10余0,
∴840与1764的最大公约数是84.
(2)f(x)=2x4+3x3+5x-4=[(2x+3)x•x+5]x-4
当x=2时
V0=2;
V1=2•V0+3=7;
V2=2•V1=14;
V3=2•V2+5=33;
V4=2•V3-4=62;
故x=2时的函数值为62.
【点睛】本题考查算法的应用,考查辗转相除法和秦九韶算法,解题时按照各自算法计算既要即可.
18.已知函数.
(1)若,都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;
(2)若,都是从区间上任取的一个数,求成立的概率.
【答案】(1)(2)
【解析】
试题分析:
(1)基本事件总数为个.函数有零点的条件为.,,,,,,,,,,,,则函数有零点的概率为.
(2)由几何概型的计算公式可得事件“”的概率为.
试题解析:
解:(1),都是从0,1,2,3,4五个数中任取的一个数,则基本事件总数为个.
函数有零点的条件为,即.因为事件“”包含,,,,,,,,,,,,
所以事件“”的概率为,即函数有零点的概率为.
(2),都是从区间上任取的一个数,,即,此为几何模型,如图可知,事件“”的概率为.
点睛:“几何概型”与“古典概型”的区别:基本事件的个数前者是无限的,后者是有限的.
古典概型计算三步曲:第一,本试验是否是等可能的;第二,本试验的基本事件有多少个;第三,事件A是什么,它包含的基本事件有多少个.
几何概型的试验中,事件A的概率P(A)只与子区域A的几何度量(长度、面积或体积)成正比,而与A的位置和形状无关.
19.已知关于的二次函数,设集合,,分别从集合和中随机取一个数作为和.
(1)求函数有零点的概率;
(2)求函数在区间上是增函数概率.
【答案】(1)(2)
【解析】
【分析】
(1)先将所有可能的情况枚举,再分析满足的情况数即可.
(2) 先将所有可能的情况枚举,再分析满足对称轴的情况即可.
【详解】共有,,,,,,,,,,,,,,,15种情况.
(1).
有,,,,,6种情况,
所以函数有零点的概率为.
(2)对称轴则,
有,,,,,,,,,,,,13种情况,
函数在区间上是增函数的概率为.
【点睛】本题主要考查了利用枚举法解决古典概型的问题,同时也考查了二次函数的性质,属于基础题.
20.某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成,,,,,六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
(1)求分数内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试成绩的中位数;
(3)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率.
【答案】(1)见解析(2) (3)
【解析】
分析:(1)利用所有小矩形的面积之和为,求得分数在内的频率,再根据小矩形的高,即可补全频率分布直方图;
(2)根据中位数的左、右两边的小矩形的面积之和相等,即可求出中位数;
(3)计算从第一组和第六组所有人数中任取
人的取法总数,利用古典概型的概率计算公式,即可求解.
详解:(1)设分数在内的频率为,根据频率分布直方图,
则有,可得,
所以频率分布直方图为:
(2)以中位数为准做一条垂直于横轴的直线,这条直线把频率分布直方图分成面积相等的两个部分,由频率分布直方图知中位数要把最高的小长方形三等分,
所以中位数是,所以估计本次考试成绩的中位数为
(3)设所抽取2人成绩之差绝对值大于10为事件,
第1组学生数:人(设为1,2,3,4,5,6)
第6组学生数:人(设为)
所有基本事件有:12,13,14,15,16,,23,24,25,26,,,,34,35,36,,,,45,46,,,,56,,,,,,,,,共有35种,
事件包括的基本事件有:,,,,,,,,,,,,,,,共有18种
所以.
点睛:本题考查了利用样本估计总体的综合应用问题,以及古典概型及其概率的计算问题,对弈频率分布直方图,应注意:1、用样本估计总体是统计的基本思想,而利用频率分布表和频率分布直方图来估计总体则是用样本的频率分布去估计总体分布的两种主要方法.分布表在数量表示上比较准确,直方图比较直观.2、频率分布表中的频数之和等于样本容量,各组中的频率之和等于1
;在频率分布直方图中,各小长方形的面积表示相应各组的频率,所以,所有小长方形的面积的和等于1.
21.某音乐院校举行“校园之星”评选活动,评委由本校全体学生组成,对两位选手,随机调查了20个学生的评分,得到下面的茎叶图:
所得分数
低于60分
60分到79分
不低于80分
分流方向
淘汰出局
复赛待选
直接晋级
(1)通过茎叶图比较两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
(2)举办方将会根据评分结果对选手进行三向分流,根据所得分数,估计两位选手中哪位选手直接晋级的概率更大,并说明理由.
【答案】(1)选手所得分数的平均值高于选手所得分数的平均值;选手所得分数比较集中,选手所得分数比较分散.(2) 选手直接晋级的概率更大.理由见解析
【解析】
【分析】
(1)根据茎叶图中数据的分布特征,可直接得出结论;
(2)用表示事件“选手直接晋级”,表示事件“选手直接晋级”,根据茎叶图中的数据,计算概率,即可得出结果.
【详解】(1)通过茎叶图可以看出,选手所得分数的平均值高于选手所得分数的平均值;选手所得分数比较集中,选手所得分数比较分散.
(2)选手直接晋级的概率更大.
用表示事件“选手直接晋级”,表示事件“选手直接晋级”.由茎叶图得
的估计值为 ,
的估计值为 ,
所以,选手直接晋级的概率更大.
【点睛】本题主要考查茎叶图的特征,以及古典概型的问题,熟记概率的计算公式即可,属于常考题型.
22.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(吨)与相应的生产能耗(吨)标准煤的几组对照数据.
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出回归方程;
(3)已知该厂技改前吨甲产品的生产能耗为吨标准煤.试根据(2)求出的线性回归方程,预测生产吨甲产品的生产能耗比技改前降低多少吨标准煤?(注:,)
【答案】(1)见解析.(2).(3)吨.
【解析】
【分析】
(1)直接描点即可
(2)计算出平均数,,及,,利用公式即可求得,问题得解.
(3)将代入可得,结合已知即可得解.
【详解】解:(1)把所给的四对数据写成对应的点的坐标,在坐标系中描出来,得到散点图;
(2)计算,
,
,
,
∴回归方程的系数为: .
,∴所求线性回归方程为;
(3)利用线性回归方程计算时,,
则,即比技改前降低了19.65吨.
【点睛】本题主要考查了线性回归方程的求法,考查计算能力,还考查了线性回归方程的应用,属于中档题.