- 476.50 KB
- 2021-05-12 发布
- 1 -
第 2 课时 对数函数的图象与性质的应用
学 习 目 标 核 心 素 养
1.能正确判断图象之间的变换关系.(重点)
2.理解并掌握对数函数的单调性.(重点)
3.会用对数函数的相关性质解综合题.(难点)
通过学习本节内容,提升学生的直观
想象、逻辑推理、数学运算的核心素
养.
画出对数函数 y=log2x,y=log x 的图象,说出该函数的性质,探究对数型函数 y=
loga(x2-2x-3)的一般性质(定义域、值域、单调性等).
1.平移变换
当 b>0 时,将 y=logax 的图象向左平移 b 个单位,得到 y=loga(x+b)的图象;向右平
移 b 个单位,得到 y=loga(x-b)的图象.当 b>0 时,将 y=loga x 的图象向上平移 b 个单位,
得到 y=logax+b 的图象,将 y=logax 的图象向下平移 b 个单位,得到 y=logax-b 的图
象.
2.对称变换
要得到 y=loga
1
x的图象,应将 y=loga x 的图象关于 x 轴对称.
为了得到函数 y=lg
x+3
10 的图象,只需把函数 y=lg x 的图象上所有的点 .
向左平移 3 个单位,再向下平移 1 个单位 [y=lg
x+3
10 =lg (x+3)-1,故将 y=lgx
向左平移 3 个单位,再向下平移 1 个单位.]
对数函数的图象
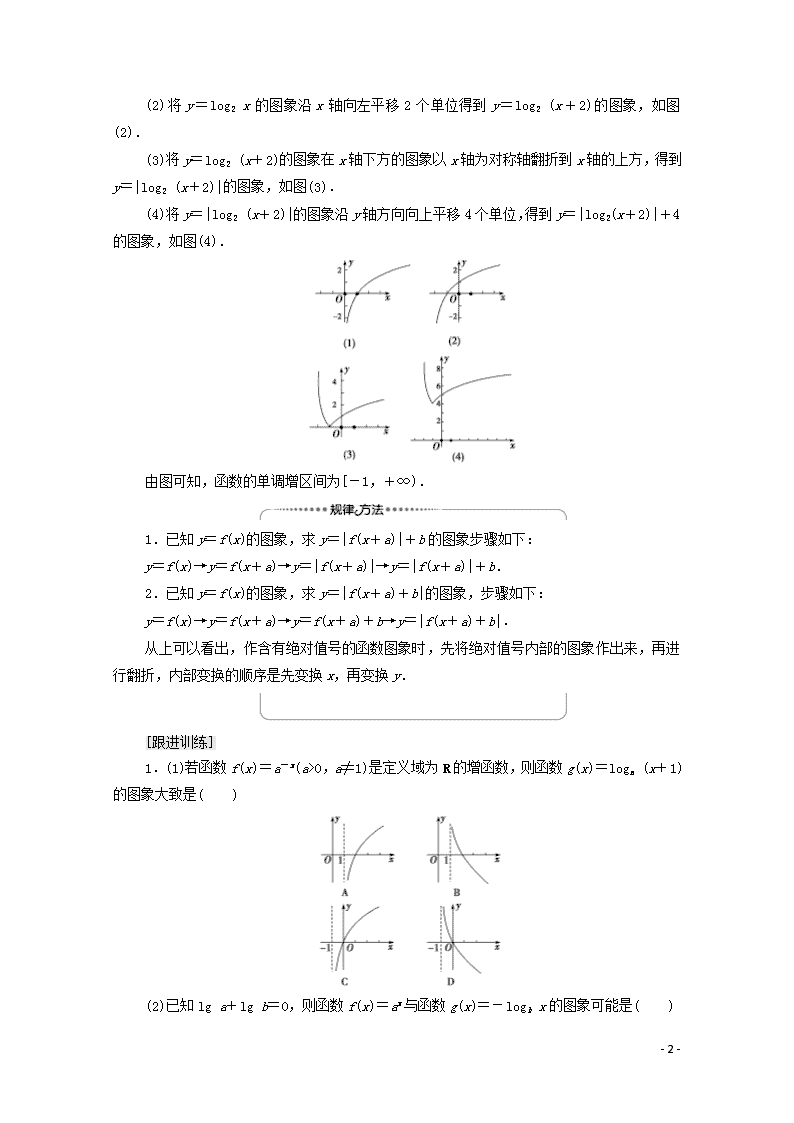
【例 1】 作出函数 y=|log2 (x+2)|+4 的图象,并指出其单调增区间.
[思路点拨] 可先作出 y=log2 x 的图象,再左移 2 个单位得到 y=log2 (x+2),通过翻
折变换得到 y=|log2 (x+2)|,再向上平移 4 个单位即可.
[解] 步骤如下:
(1)作出 y=log2 x 的图象,如图(1).
(2)将 y=log2 x 的图象沿 x 轴向左平移 2 个单位得到 y=log2 (x+2)的图象,如图
- 2 -
(2).
(3)将 y=log2 (x+2)的图象在 x 轴下方的图象以 x 轴为对称轴翻折到 x 轴的上方,得到
y=|log2 (x+2)|的图象,如图(3).
(4)将 y=|log2 (x+2)|的图象沿 y 轴方向向上平移 4 个单位,得到 y=|log2(x+2)|+4
的图象,如图(4).
由图可知,函数的单调增区间为[-1,+∞).
1.已知 y=f(x)的图象,求 y=|f(x+a)|+b 的图象步骤如下:
y=f(x)→y=f(x+a)→y=|f(x+a)|→y=|f(x+a)|+b.
2.已知 y=f(x)的图象,求 y=|f(x+a)+b|的图象,步骤如下:
y=f(x)→y=f(x+a)→y=f(x+a)+b→y=|f(x+a)+b|.
从上可以看出,作含有绝对值号的函数图象时,先将绝对值号内部的图象作出来,再进
行翻折,内部变换的顺序是先变换 x,再变换 y.
[跟进训练]
1.(1)若函数f(x)=a-x(a>0,a≠1)是定义域为 R 的增函数,则函数 g(x)=loga (x+1)
的图象大致是( )
(2)已知 lg a+lg b=0,则函数 f(x)=ax 与函数 g(x)=-logb x 的图象可能是( )
- 3 -
(1)D (2)B [(1)因为函数 f(x)=a-x 是定义域为 R 的增函数,所以 01;当 b>1 时,00⇒x2<9⇒-30.
又(2-x1)(2+x2)>0,(2+x1)(2-x2)>0,
∴
2-x12+x2
2+x12-x2>1,
∴lg
2-x12+x2
2+x12-x2>0.
从而 f(x1)>f(x2),故 f(x)在(-2,2)上为减函数.
对数函数性质的综合应用
1常见的命题方式,对数函数常与函数的奇偶性、单调性、最大小值以及不等式
等问题综合命题,求解中通常会涉及对数运算.
2解此类问题的基本思路,首先要将所给的条件进行转化,然后结合涉及的知识点,
明确各知识点的应用思路、化简方向,与所求目标建立联系,从而找到解决问题的思路.
[跟进训练]
3.已知函数 f(x)=loga (x+1)(a>1),若函数 y=g(x)图象上任意一点 P 关于原点对称
的点 Q 在函数 f(x)的图象上.
(1)写出函数 g(x)的解析式;
(2)当 x∈[0,1)时总有 f(x)+g(x)≥m 成立,求 m 的取值范围.
[解] (1)设 P(x,y)为 g(x)图象上任意一点,则 Q(-x,-y)是点 P 关于原点的对称点,
∵Q(-x,-y)在 f(x)的图象上,
∴-y=loga(-x+1),即 y=g(x)=-loga(1-x).
(2)f(x)+g(x)≥m,即 loga
x+1
1-x≥m.
- 6 -
设 F(x)=loga
1+x
1-x=loga(-1+
2
1-x),x∈[0,1),
由题意知,只要 F(x)min≥m 即可.
∵F(x)在[0,1)上是增函数,
∴F(x)min=F(0)=0.
故 m 的取值范围为(-∞,0].
解对数不等式(或方程)
[探究问题]
1.对数函数的单调性,内容是什么?
[提示] 对数函数 y=loga x,当 a>1 时,在(0,+∞)上单调递增,当 00 且 a≠1,x>0.
【例 4】 已知函数 f(x)=loga(1+x),g(x)=loga(1-x),其中(a>0 且 a≠1),设 h(x)
=f(x)-g(x).求函数 h(x)的定义域,判断 h(x)的奇偶性,并说明理由.
[思路点拨] 根据对数函数的单调性求解即可,但应注意定义域的限制,在底不确定时
应注意讨论.
[解] ∵f(x)=loga(1+x)的定义域为{x|x>-1},
g(x)=loga(1-x)的定义域为{x|x<1},
∴h(x)=f(x)-g(x)的定义域为{x|x>-1}∩{x|x<1}={x|-11),求 f(x)的定义域.
[解] 因为 f(x)=loga
1+x
1-x,
所以
1+x
1-x>0,即Error!或Error!
所以-10,所以 f(x1)-f(x2)<0,即 f(x1)
相关文档
- 2019年高中政治学业水平考试专题复2021-05-12 22:11:4025页
- 高中生文艺进社区社会实践活动总结2021-05-12 22:11:122页
- 2019-2020学年苏教版高中生物必修2021-05-12 22:10:229页
- 2020高中生物教师个人工作总结范文2021-05-12 22:09:007页
- 北京市2020年第一次普通高中学业水2021-05-12 22:06:0712页
- 高中语文精品课件-第11课 就任北2021-05-12 22:05:2029页
- 高中2020年度工作总结2021-05-12 22:00:0811页
- 2020新教材高中物理第十章静电场中2021-05-12 21:55:5710页
- 2019-2020学年历史高中人教版必修12021-05-12 21:53:416页
- 2017高中语文综合质量检测新人教版2021-05-12 21:53:4016页