- 473.00 KB
- 2021-05-12 发布
高 一 年 级 月 考 三
数 学 试 题 2019.11
时间:120分钟 满分:150分
一.选择题(共12题,每题5分)
1.设集合A={-1,1,2,3,5},B={2,3,4}, ,则(A∩C)∪B=( )
A. {2} B. {2,3}
C. {-1,2,3} D. {1,2,3,4}
2.下面说法正确的是( )
A.一个算法的步骤是可逆的 B.一个算法可以无止境地运算下去
C.完成一件事情的算法有且只有一种 D.设计算法要本着简单方便的原则
3. 函数 的定义域是( )
A. B.
C. D.
4. 下列说法中不正确的是( )
A.顺序结构是由若干个依次执行的步骤组成的,每一个算法都离不开顺序结构
B.循环结构是在一些算法中从某处开始,按照一定的条件,反复执行某些步骤,所以循环结构中一定包含条件结构
C.循环结构中不一定包含条件结构
D.用程序框图表示算法,使之更加直观形象,容易理解
5.已知幂函数的图象经过点,则的值为( )
A. B. C. D. 2
6.下列程序输出的结果是( )
A. 3
B. 5
C. 7
D. 8
7.函数 的单调递减区间为( )
A. (1,+∞) B. (1,2)
C. (0,1) D. (∞,1)
8.下面程序运行后输出的结果为( )
A. 0
B. 1
C. 2
D. 4
9.函数的零点所在的一个区间是( )
A. B. C. D.
10.阅读下列程序:如果输入的则输出的( )
A.
B.
C.
D.
11.函数的零点个数为( )
A.1 B.2 C.3 D.4
12.对于任意a∈[-1,1],函数f(x)=x2+(a-4)x+4-2a的值恒大于零,那么x的取值范围是( )
A.(1,3) B.(-∞,1)∪(3,+∞)
C.(1,2) D.(3,+∞)
二.填空题(共4题,每题5分)
13.右边程序的运行结果为 .
14. .
15. 用秦九韶算法计算在x=2的值时,的值为 .
16.设函数f(x)是定义在R上的偶函数,且对任意的x∈R恒有f(x+1)=f(x-1),已知当x∈[0,1]时,f(x)=,则:
①;
②函数f(x)在(1,2)上递减,在(2,3)上递增;
③函数f(x)的最大值是1,最小值是0;
④当x∈(3,4)时,f(x)=
其中所有正确命题的序号是________.
三.解答题(共6题,第17题为10分,其余各题每题为12分)
17.已知.
(1).若,求a的值.
(2).若,求a的值.
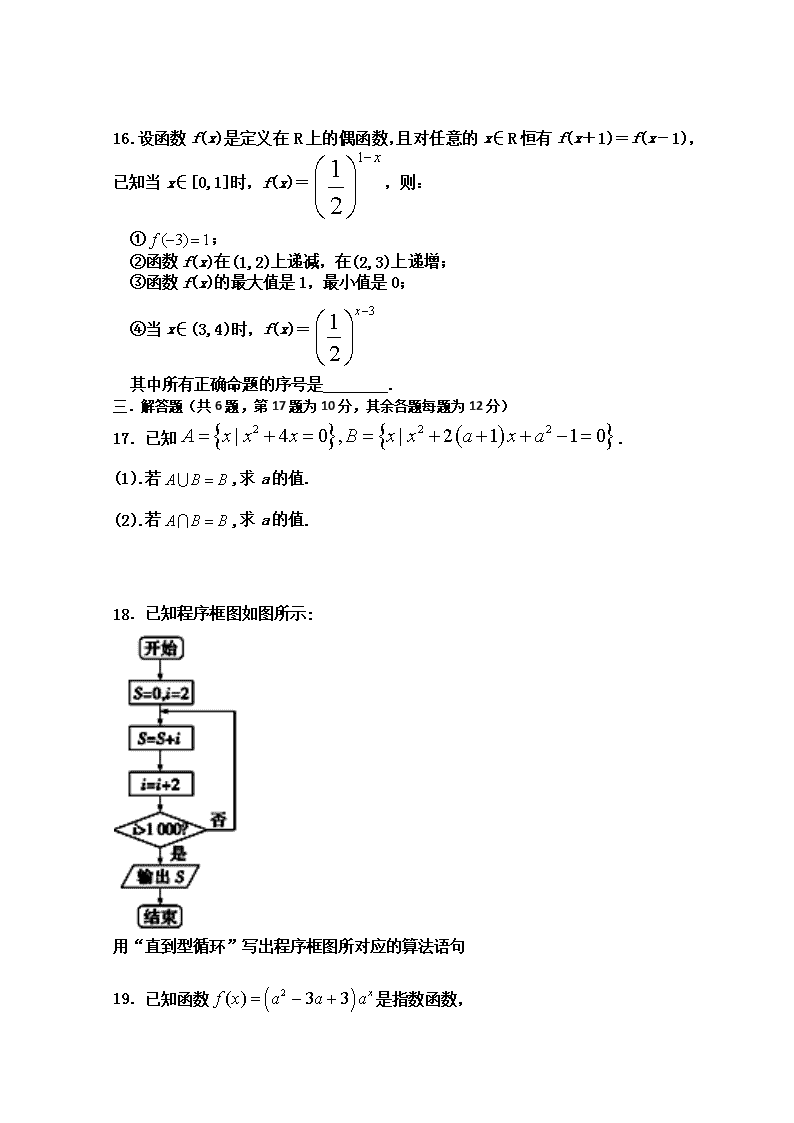
18.已知程序框图如图所示:
用“直到型循环”写出程序框图所对应的算法语句
19. 已知函数
是指数函数,
(1)求的表达式;
(2)令,解不等式
20. 已知时,函数恒有零点,求实数的取值范围.
21.某厂生产一种机器的固定成本(即固定投入)为0.5万元,但每生产100台,需增加可变成本(即另增加投入)0.25万元.市场对此产品的年需求量为500台,销售的收入函数为(万元)(),其中x是产品售出的数量(单位:百台).
(1).把利润表示为年产量的函数;
(2).年产量是多少时,工厂所得利润最大?
22.已知函数,其中为实常数.
(Ⅰ)判断的奇偶性;
(Ⅱ)若对任意,使不等式恒成立,求的取值范围.
高一月考三 数学答案2019.11
1
2
3
4
5
6
7
8
9
10
11
12
D
D
D
C
A
B
B
A
C
A
B
B
13. 1,1,1 14. 15. 33 16.①②④
17.答案:( 1).
若,则,解得
(2).若,则
①若B为空集,则,则;
②若B为单元素集合,则,
解得,将代入方程,
得,得,即,符合要求;
③若,则.
综上所述, 或.
18.答案:1.算法语句如下:
19. 答案:(1)∵ 函数是指数函数,
∴ ,
可得或(舍去),
∴ ;
(2)由题意得,,
即
即
即
或
解得或
原不等式的解集为
20. 答案:
当时,由,得,此时
当时,令,即恒有解,
即恒成立
即恒成立,
则,即.
所以,函数恒有零点时,有
21.答案:(1).,设利润函数为,所以当时,,
当时,只能售出500台
所以
综上,
(2).由(1)知
①当时,
因为抛物线开口向下,对称轴为,
所以当时,
②当时,为R上的减函数,
所以
综上所述,当时,取最大值
所以年产量为475台时,所得利润最大。
22.答案:
(Ⅰ)当时,为偶函数;当时,为非奇非偶函数;(Ⅱ)
解析:
(Ⅰ)易求得函数的定义域为,是关于原点对称的.
当时,
所以为偶函数;
当时,因为,所以不是奇函数;
因为所以,
故不是偶函数. 综合得为非奇非偶函数.
综上所述,当时,为偶函数;当时,为非奇非偶函数.
(Ⅱ)(1)当时,不等式化为即,
若,即,则矛盾.
若,即,则即解得或所以
(2)当时,不等式化为即,
若即,结合条件,得
若即,即解得 或结合条件及(1),得
若,恒成立. 综合得
(3)当时,不等式化为即,得即。结合(2)得
所以,使不等式对恒成立的的取值范围是