- 136.80 KB
- 2021-05-12 发布
等积变形问题
运用方程解决实际问题的一般过程是什么?
1、审题:分析题意,找出题中的数量及
其关系;
2、设元:选择一个适当的未知数用字母表
示(例如x);
3、列方程:根据相等关系列出方程;
4、解方程:求出未知数的值;
5、检验:检查求得的值是否正确和符合
实际情形,并写出答案。
审
设
列
解
验
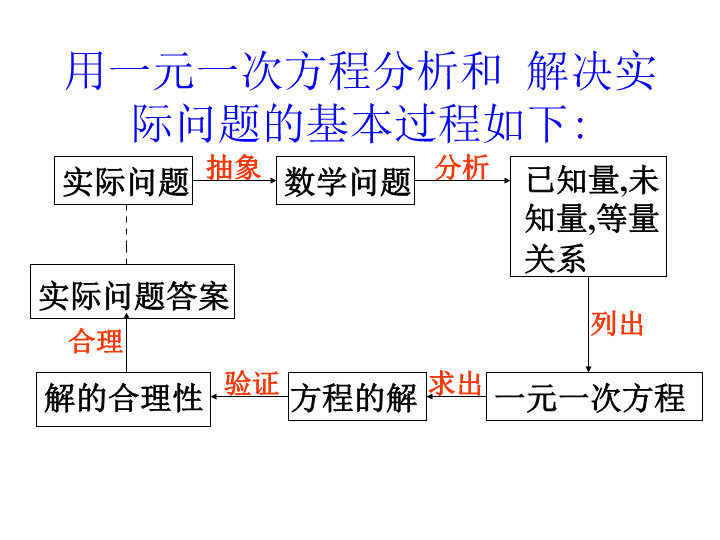
用一元一次方程分析和 解决实
际问题的基本过程如下:
实际问题 数学问题 已知量,未
知量,等量
关系
一元一次方程方程的解解的合理性
实际问题答案
抽象 分析
列出
求出验证
合理
• 例1、一标志性建筑的
底面是正方形,在其
四周铺上花岗石,形
成一个宽为3米的正方
形边框,已知铺上这
个边框恰好用了192块
边长为0.75米的正方形
花岗石,问标志性建
筑的底面边长是多少
米?
3 X
分析:若用x表示标志性建筑的底
面边长,本题的等量关系是什么?
阴影部分的面积= 192块边长为
0.75米的正方形花岗石的面积
3
怎样表示用x的代数式阴影部分的面积?
• 例1、一标志性建筑的
底面是正方形,在其四
周铺上花岗石,形成一
个宽为3米的正方形边
框,已知铺上这个边框
恰好用了192块边长为
0.75米的正方形花岗石,
问标志性建筑的底面边
长是多少米?
3 X 3
24 3 3 0.75 0.75 192x
• 例1、一标志性建筑的
底面是正方形,在其四
周铺上花岗石,形成一
个宽为3米的正方形边
框,已知铺上这个边框
恰好用了192块边长为
0.75米的正方形花岗石,
问标志性建筑的底面边
长是多少米?
3 X 3
4 3 3 0.75 0.75 192x
3 X 3
• 例1、一标志性建筑的
底面是正方形,在其四
周铺上花岗石,形成一
个宽为3米的正方形边
框,已知铺上这个边框
恰好用了192块边长为
0.75米的正方形花岗石,
问标志性建筑的底面边
长是多少米?
2 6 34 0.75 0.75 1922
x
3 X 3• 例1、一标志性建筑的
底面是正方形,在其四
周铺上花岗石,形成一
个宽为3米的正方形边
框,已知铺上这个边框
恰好用了192块边长为
0.75米的正方形花岗石,
问标志性建筑的底面边
长是多少米?
2 3 6 2 3 0.75 0.75 192x x
• 变式1、一标志性建筑的底
面是边长为6米正方形,在
其四周铺上花岗石,形成
一个宽为3米的正方形边框,
已知铺上这个边框恰好用
了192块正方形花岗石,问
每块正方形花岗石边长是
多少米?
3
6
设每块正方形花岗石边长是x米,怎样根据等量关系列出方程?
2 2 2192 12 6x
• 变式1、一标志性建
筑的底面是边长为6
米正方形,在其四
周铺上花岗石,形
成一个宽为3米的正
方形边框,已知铺
上这个边框恰好用
了x块边长为0.75米
的正方形花岗石,
求X是多少?
3
怎样根据等量关系列出方程?
2 2 20.75 12 6x
小结:
1、列方程解决有关实际问题时,清楚
地分辨量之间的关系,尤其是等量关系
是建立方程的关键。解题中的检验对确
保答案的正确和合理很有帮助,但具体
过程可以不写。
2、对于等积变形问题,它的基本数量
关系是相关的面积公式,相等关系的特
征是存在不变量,也就是用不同的方法
来计算阴影部分的面积,面积不变。
例4 .学校组织植树活动,已
知在甲处植树的有23人,在
乙处植树的有17人.现调20
人去支援,使在甲处植树的
人数是乙处植树人数的2倍,
应调往甲,乙两处各多少人?
甲处 乙处
原有人数
增加人数
增加后人数 17+20-x23+x
20-xx
23 17
分析 设应调往甲处
x人,题目中所涉及
的有关数量及其关
系可以用右表表示:
甲处增加后人数=2×乙处增加后人数
想一想:如
果调往乙处
的人数为x,
方程应怎样
列?
在解决实际问题时,我们一般可以
通过分析实际问题, 抽象出数学问题,
然后运用数学思想方法解决问题.用列
表分析数量关系是常用的方法.
相关文档
- 七年级上册数学课件《应用一元一次2021-05-12 11:48:208页
- 七年级上册数学课件《有理数》 人2021-05-12 02:17:1413页
- 七年级上册数学课件《整式的加减》2021-05-11 21:42:5712页
- 七年级上册数学课件《普查与抽样调2021-05-11 17:11:0019页
- 七年级上册数学课件《应用一元一次2021-05-11 02:07:318页
- 七年级上册数学课件《角》 (2)_2021-05-10 12:43:0425页
- 七年级上册数学课件《有理数的乘方2021-05-09 02:24:3024页
- 七年级上册数学课件《数轴》 (1)_2021-05-08 19:30:4016页
- 七年级上册数学课件《整式》 人教2021-05-08 10:58:4015页
- 七年级上册数学课件《探索与表达规2021-05-07 20:40:3912页