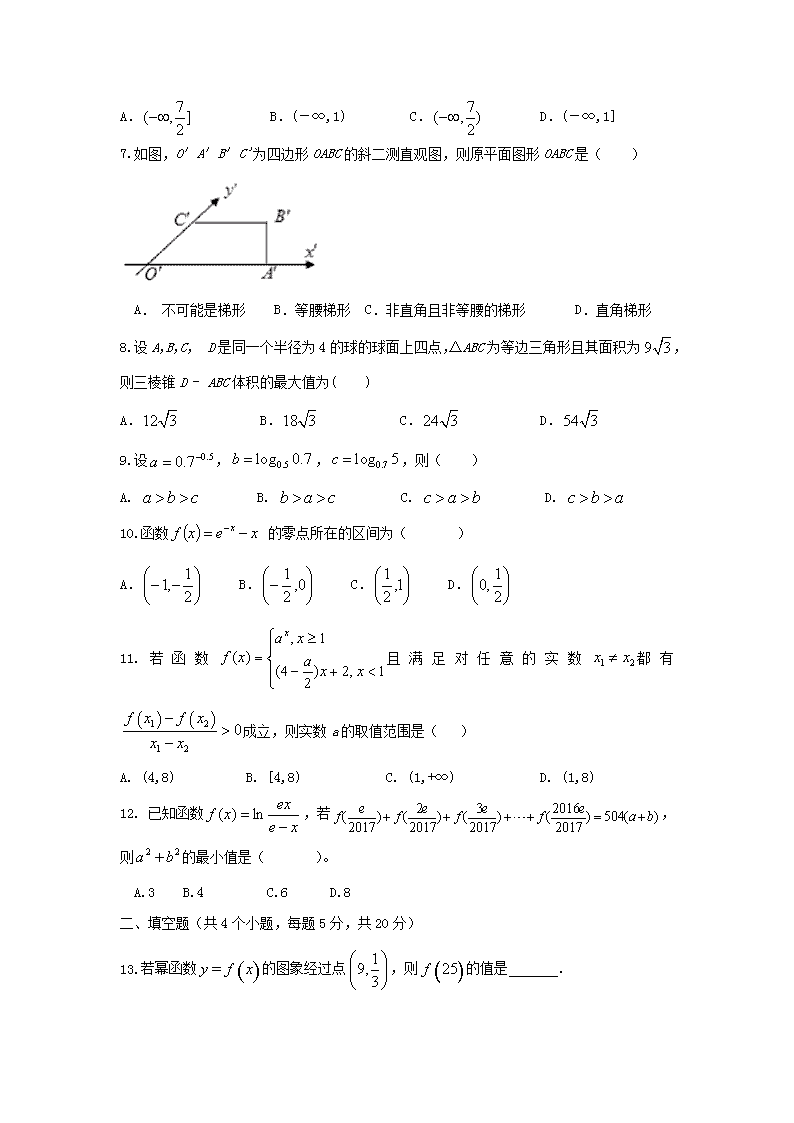2018-2019学年河北省安平中学高一上学期期中考试数学试题（实验班） 8页

‎2018-2019学年河北省安平中学高一上学期期中考试数学试题（实验班）‎ 参考公式：‎ V柱体= sh ‎ ‎ 圆台侧面积 ‎ ‎． 球表面积 ‎ 一、 选择题（本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1.函数的零点是（ ）‎ A（-2，0） B.-2 C.（0，-2） D.0‎ ‎2.若正棱锥底面边长与侧棱长相等，则该棱锥一定不是（　　）‎ A.三棱锥  B.四棱锥 C.五棱锥 D.六棱锥 ‎3.已知球面上有A、B、C三点，且AB=AC=，BC=2，球心到平面ABC的距离为，则球的体积为 （ ） ‎ A B C D ‎4.在同一坐标系中，函数与的图象大致是（ ）‎ A．B． C. D．‎ ‎5．幂函数在(0,+∞)上单调递增，则m的值为（ ）‎ A. 2 B. 3 C. 4 D. 2或4‎ ‎6.若关于x的不等式的解集包含区间(0,1)，则a的取值范围为（ ）‎ A． B．(－∞,1) C． D．(－∞,1] ‎ ‎7.如图，O′A′B′C'为四边形OABC的斜二测直观图，则原平面图形OABC是（ ）‎ A． 不可能是梯形 B．等腰梯形 C．非直角且非等腰的梯形 D．直角梯形 ‎ ‎8.设A，B，C， D是同一个半径为4的球的球面上四点，△ABC为等边三角形且其面积为，则三棱锥D - ABC体积的最大值为(　　)‎ A． B． C． D．‎ ‎9.设，，，则（ ）‎ A. B. C. D. ‎ ‎10.函数 的零点所在的区间为（    ）‎ A． B． C． D． ‎ ‎11.若函数且满足对任意的实数都有成立，则实数a的取值范围是（ ）‎ A. (4,8) B. [4,8) C. (1,+∞) D. (1,8)‎ 12. 已知函数，若，则的最小值是（ ）。‎ A.3 B.4 C.6 D.8‎ 二、 填空题（共4个小题，每题5分，共20分）‎ ‎13.若幂函数的图象经过点，则的值是 ．‎ ‎14..计算_______．‎ ‎15.函数的单调递增区间为_______．‎ 16. 已知函数，则方程 的解的个数为_______．‎ 三、解答题（共70分，解答题应写出必要的文字说明和演算步骤）‎ ‎17.(本小题满分10分）已知幂函数，经过点，试确定的值，并求满足条件的实数a的取值范围．‎ ‎18.(本小题满分12分）已知函数，其中.‎ ‎（1）求函数的最大值和最小值；‎ ‎（2）若实数满足：恒成立，求a的取值范围.‎ ‎19.（本小题满分12分）已知函数（）‎ ‎（1）求函数的定义域；‎ ‎（2）若函数的最小值为－4，求a的值.‎ ‎20.（本小题满分12分）如图，在四边形ABCD中，∠DAB=90°，∠ADC=135°，AB=5，CD=，AD=2，求四边形绕AD旋转一周所围成几何体的表面积及体积．‎ ‎21.（本小题满分12分）已知函数 ‎（1）在所给的平面直角坐标系中画出函数的图象，并根据图象写出的单调区间；‎ ‎（2）若函数有四个零点，求实数的取值范围. ‎ ‎ (3）解不等式 ‎22.(本小题满分12分)已知函数为奇函数．‎ ‎(1)求常数的值；‎ ‎(2)设，证明函数在(1，＋∞)上是减函数；‎ ‎(3)若函数，且在区间[3,4]上没有零点，求实数的取值范围.‎ ‎ 安平中学2018-2019学年第一学期期中考试 高一实验部数学试题答案 一、 选择题BDBBC DDBAC BD 二、 填空题 6 5‎ 三、解答题 ‎17.(本小题满分10分）解：因为幂函数经过点，即，解得 或又,‎ ‎，则函数的定义域为，并且在定义域内为增函数。‎ 由得，解得。的取值范围是 ‎18.解：（1）.令，∵，∴.‎ 令.‎ 当时，是减函数；当时，是增函数.‎ ‎∴，.‎ ‎（2）∵恒成立，即恒成立，∴恒成立.‎ 由（1）知，∴.故的取值范围为.‎ ‎19.解：（1）要使函数有意义，则有解之得，所以函数的定义域为.‎ ‎（2）‎ ‎∵，∴‎ ‎∵，∴，‎ ‎∴，由，得，∴‎ ‎20.【解答】解：四边形ABCD绕AD旋转一周所成的 几何体，如右图：‎ S表面=S圆台下底面+S圆台侧面+S圆锥侧面 ‎=πr22+π（r1+r2）l2+πr1l1‎ ‎=‎ ‎=‎ ‎=．‎ 体积V=V圆台﹣V圆锥 ‎= [25π++4π]×4﹣×2π×2×2‎ ‎=×39π×4﹣×8π ‎=．‎ 所求表面积为：，体积为：．‎ ‎21解：（1）函数的图象如图所示，由图象可得函数的单调递增区间为和，单调递减区间为和；‎ ‎（2）由函数的图象可知，当且仅当时，函数有四个零点，‎ ‎∴实数的取值范围为.‎ （3） 由或或 ‎ 得或或 ‎ 所以元不等式的解集为 ‎22.(1)解：∵f (x)＝log为奇函数，‎ ‎∴f(－x)＝－f(x)，‎ 即log＝－log＝log，‎ ‎∴＝，即1－k2x2＝1－x2，整理得k2＝1.‎ ‎∴k＝－1(k＝1使f(x)无意义而舍去)．‎ ‎(2)证明：由(1)得，k＝－1，h(x)＝＝＝1＋，任取x1，x2∈(1，＋∞)，且x10，x2－1>0，‎ ‎∴h(x2)－h(x1)＝<0，‎ ‎∴h(x1)>h(x2)，‎ ‎∴函数y＝h(x)在(1，＋∞)是减函数．‎ ‎(3)解：由(2)知，f(x)在(1，＋∞)上递增，‎ 所以g(x)＝f(x)－x＋m在[3,4]递增．‎ ‎∵g(x)在区间[3,4]上没有零点．‎ ‎∴g(3)＝log－3＋m＝－＋m>0或g(4)＝log－4＋m＝log－＋m<0，‎ ‎∴m>或m<－log.‎