- 180.00 KB
- 2021-05-12 发布
课时分层作业(二十一) 函数的单调性
(建议用时:40分钟)
一、选择题
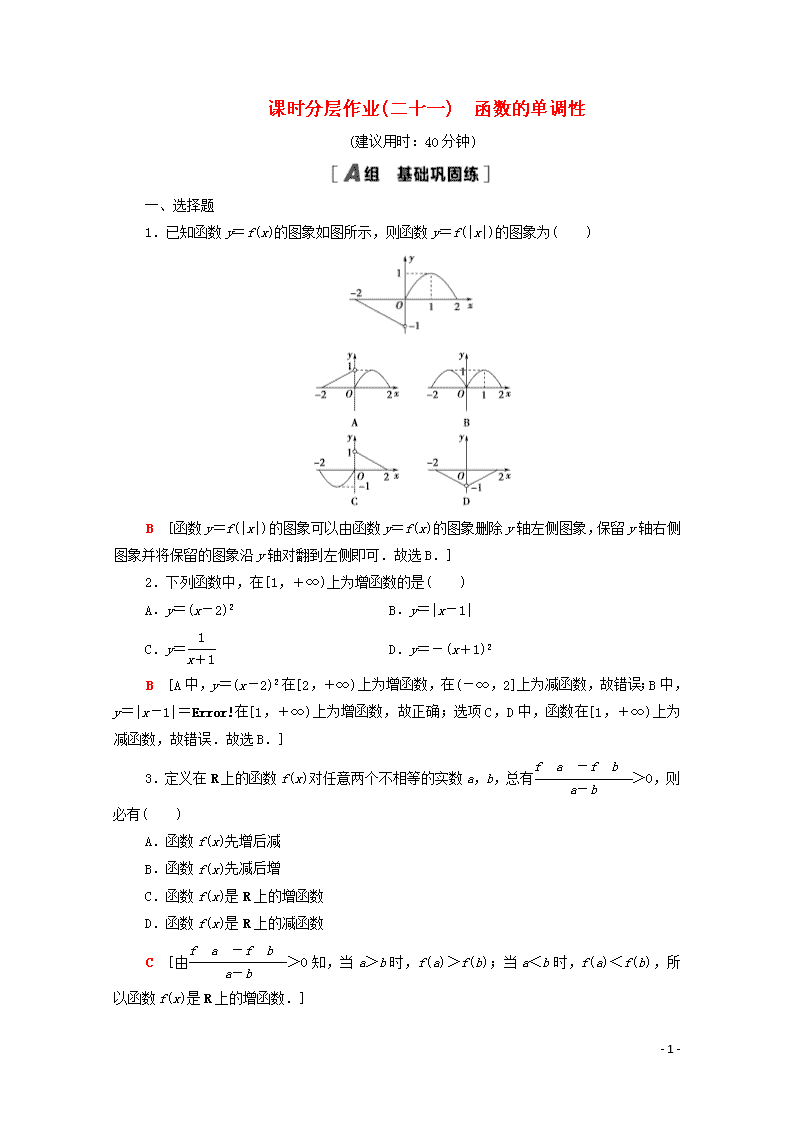
1.已知函数y=f(x)的图象如图所示,则函数y=f(|x|)的图象为( )
B [函数y=f(|x|)的图象可以由函数y=f(x)的图象删除y轴左侧图象,保留y轴右侧图象并将保留的图象沿y轴对翻到左侧即可.故选B.]
2.下列函数中,在[1,+∞)上为增函数的是( )
A.y=(x-2)2 B.y=|x-1|
C.y= D.y=-(x+1)2
B [A中,y=(x-2)2在[2,+∞)上为增函数,在(-∞,2]上为减函数,故错误;B中,y=|x-1|=在[1,+∞)上为增函数,故正确;选项C,D中,函数在[1,+∞)上为减函数,故错误.故选B.]
3.定义在R上的函数f(x)对任意两个不相等的实数a,b,总有>0,则必有( )
A.函数f(x)先增后减
B.函数f(x)先减后增
C.函数f(x)是R上的增函数
D.函数f(x)是R上的减函数
C [由>0知,当a>b时,f(a)>f(b);当a<b时,f(a)<f(b),所以函数f(x)是R上的增函数.]
- 5 -
4.已知f(x)在区间(0,+∞)上是减函数,那么f(a2-a+1)与f的大小关系是( )
A.f(a2-a+1)>f
B.f(a2-a+1)≤f
C.f(a2-a+1)≥f
D.f(a2-a+1),则a的取值范围是.]
三、解答题
9.已知函数f(x)=.
(1)求f(x)的定义域;
(2)证明函数f(x)=在[1,+∞)上是单调增函数.
[解] (1)由题意知x+1≠0,
即x≠-1.
所以f(x)的定义域为(-∞,-1)∪(-1,+∞).
(2)证明:任取x1,x2∈[1,+∞),且x10.
又∵x1,x2∈[1,+∞),
∴x2+1>0,x1+1>0.
∴f(x2)-f(x1)>0,
∴f(x2)>f(x1).
∴函数f(x)=在[1,+∞)上是单调增函数.
10.作出函数f(x)=+的图象,并指出函数f(x)的单调区间.
[解] 原函数可化为
f(x)=|x-3|+|x+3|=
图象如图所示.
- 5 -
由图象知,函数的单调区间为(-∞,-3],[3,+∞).
其中单调减区间为(-∞,-3],单调增区间为[3,+∞).
1.已知f(x)为R上的减函数,则满足f1.解得-10,
又(x2+2)(x1+2)>0.
(1)若a<,则1-2a>0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2),
则f(x)在(-2,+∞)上为减函数.
(2)若a>,则1-2a<0.
- 5 -
∴f(x1)-f(x2)<0,
即f(x1)时,f(x)在(-2,+∞)上为增函数.
- 5 -
相关文档
- 2020_2021学年新教材高中数学第5章2021-05-08 19:20:079页
- 2020_2021学年新教材高中数学第5章2021-05-06 17:48:418页
- 2018届二轮复习函数概念与性质课件2021-04-23 19:37:3743页
- 2020_2021学年新教材高中数学第三2021-04-19 15:13:5542页
- 高中数学第5章函数概念与性质课时2021-04-18 01:39:455页
- 高中数学第5章函数概念与性质课时2021-04-18 00:12:335页
- 2020_2021学年新教材高中数学第5章2021-04-16 22:49:007页
- 高中数学第5章函数概念与性质课时2021-04-15 22:25:174页
- 高中数学第5章函数概念与性质课时2021-04-14 16:35:085页
- 2020_2021学年新教材高中数学第三2021-04-13 23:25:0836页