2020高中数学第1课时 并集、交集及其应用学案 新人教A版必修1 5页

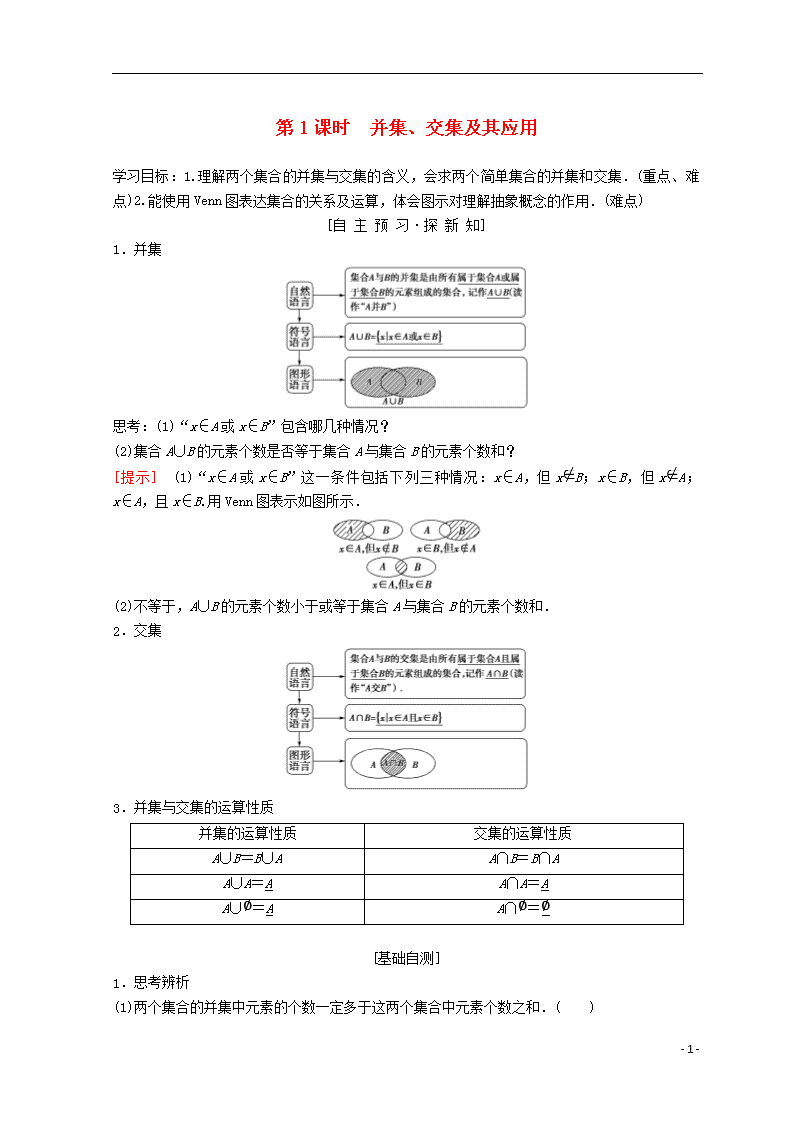
第1课时　并集、交集及其应用 学习目标：1.理解两个集合的并集与交集的含义，会求两个简单集合的并集和交集．(重点、难点)2.能使用Venn图表达集合的关系及运算，体会图示对理解抽象概念的作用．(难点)‎ ‎[自 主 预 习·探 新 知]‎ ‎1．并集 思考：(1)“x∈A或x∈B”包含哪几种情况？‎ ‎(2)集合A∪B的元素个数是否等于集合A与集合B的元素个数和？‎ ‎[提示]　(1)“x∈A或x∈B”这一条件包括下列三种情况：x∈A，但xB；x∈B，但xA；x∈A，且x∈B.用Venn图表示如图所示．‎ ‎(2)不等于，A∪B的元素个数小于或等于集合A与集合B的元素个数和．‎ ‎2．交集 ‎3．并集与交集的运算性质 并集的运算性质 交集的运算性质 A∪B＝B∪A A∩B＝B∩A A∪A＝A A∩A＝A A∪∅＝A A∩∅＝∅‎ ‎[基础自测]‎ ‎1．思考辨析 ‎(1)两个集合的并集中元素的个数一定多于这两个集合中元素个数之和．(　　)‎ - 5 -‎ ‎(2){1,2,3,4}∪{0,2,3}＝{1,2,3,4,0,2,3}．(　　)‎ ‎(3)A∩B是由属于A且属于B的所有元素组成的集合．(　　)‎ ‎[答案]　(1)×　(2)×　(3)√‎ ‎2．设集合M＝{－1,0,1}，N＝{0,1,2}，则 M∪N＝________，M∩N＝________.‎ ‎{－1,0,1,2}　{0,1}　[∵M＝{－1,0,1}，N＝{0,1,2}，∴M∩N＝{0,1}，M∪N＝{－1,0,1,2}．]‎ ‎3．若集合A＝{x|－32}，则A∪B＝________. ‎ ‎【导学号：37102049】‎ ‎{x|x>－3}　[如图：‎ 故A∪B＝{x|x>－3}．]‎ ‎[合 作 探 究·攻 重 难]‎ 并集概念及应用 ‎　(1)设集合M＝{x|x2＋2x＝0，x∈R}，N＝{x|x2－2x＝0，x∈R}，则M∪N＝(　　) ‎ ‎【导学号：37102050】‎ A．{0}　　　　　　　　　 B．{0,2}‎ C．{－2,0} D．{－2,0,2}‎ ‎(2)已知集合M＝{x|－35}，则M∪N＝(　　)‎ A．{x|x<－5或x>－3}‎ B．{x|－55}‎ ‎(1)D　(2)A　[M＝{x|x2＋2x＝0，x∈R}＝{0，－2}，N＝{x|x2－2x＝0，x∈R}＝{0,2}，故M∪N＝{－2,0,2}，故选D.‎ ‎(2)在数轴上表示集合M，N，如图所示， 则M∪N＝{x|x<－5或x>－3}．‎ ‎]‎ ‎[规律方法]　求集合并集的两种基本方法 (1)定义法：若集合是用列举法表示的，可以直接利用并集的定义求解；‎ (2)数形结合法：若集合是用描述法表示的由实数组成的数集，则可以借助数轴分析法求解.‎ ‎[跟踪训练]‎ ‎1．设S＝{x|x<－1或x>5}，T＝{x|a－1‎ D．a<－3或a>－1‎ A　[在数轴上表示集合S，T如图所示．因为S∪T＝R，由数轴可得，解得－32‎ C．a≥－1 D．a>－1‎ D　[因为A∩B≠∅，所以集合A，B有公共元素，在数轴上表示出两个集合，如图所示，易知a>－1.]‎ 集合交、并运算的性质及综合应用 ‎[探究问题]‎ ‎1．设A、B是两个集合，若已知A∩B＝A，A∪B＝B，则集合A与B具有什么关系？‎ 提示：A∩B＝A⇔A∪B＝B⇔A⊆B.‎ ‎2．若A∩B＝A∪B，则集合A，B间存在怎样的关系？‎ 提示：若A∩B＝A∪B，则集合A＝B.‎ ‎　已知集合A＝{x|－32k－1时，k<2，满足A∪B＝A.‎ ‎(2)当B≠∅时，要使A∪B＝A，‎ 只需解得2≤k≤.‎ 综合(1)(2)可知k≤.‎ 母题探究：1.把本例条件“A∪B＝A”改为“A∩B＝A”，试求k的取值范围．‎ ‎[解]　由A∩B＝A可知A⊆B.‎ 所以，即所以k∈∅.‎ 所以k的取值范围为∅.‎ ‎2．把本例条件“A∪B＝A”改为“A∪B＝{x|－3