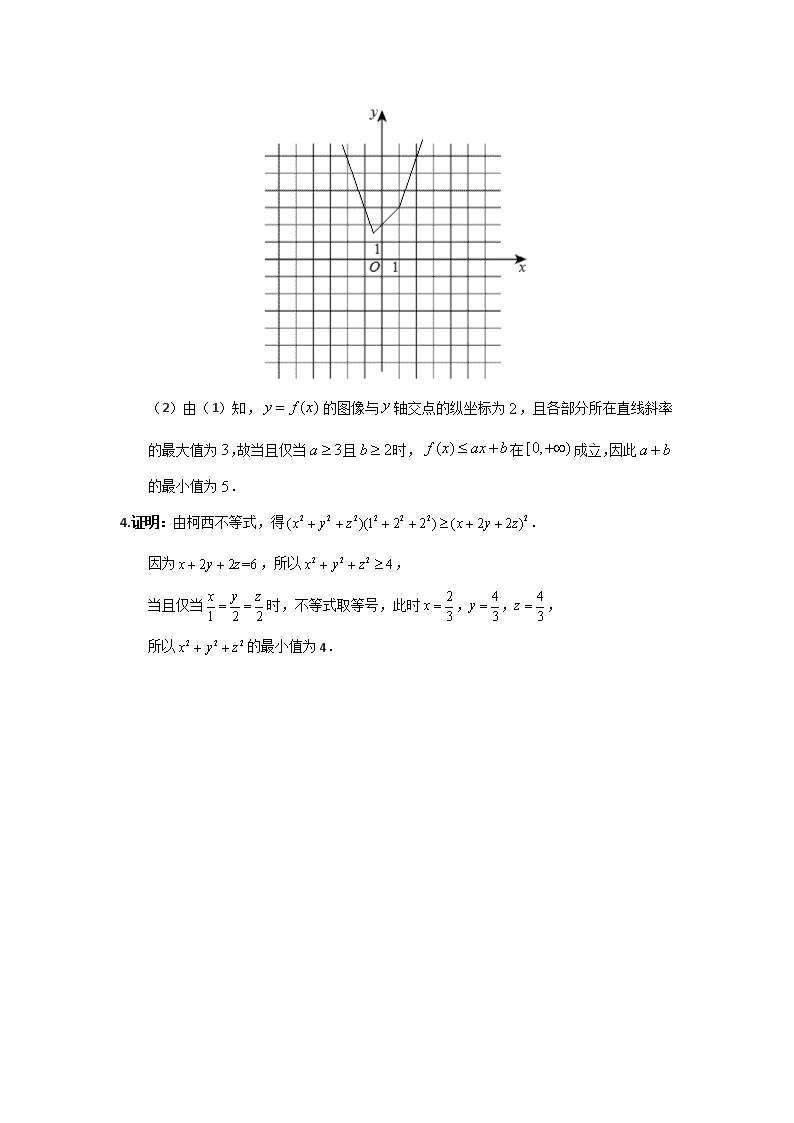- 87.59 KB
- 2021-05-11 发布
《2018年高考文科数学分类汇编》
第十四篇:不等式选讲
解答题
1.【2018全国一卷23】已知.
(1)当时,求不等式的解集;
(2)若时不等式成立,求的取值范围.
2.【2018全国二卷23】设函数.
(1)当时,求不等式的解集;
(2)若,求的取值范围.
3.【2018全国三卷23】设函数.
(1)画出的图像;
(2)当,,求的最小值.
4.【2018江苏卷21D】若x,y,z为实数,且x+2y+2z=6,求的最小值.
参考答案
解答题
1.解: (1)当时,,即
故不等式的解集为.
(2)当时成立等价于当时成立.
若,则当时;
若,的解集为,所以,故.
综上,的取值范围为.
2.解:(1)当时,
可得的解集为.
(2)等价于.
而,且当时等号成立.故等价于.
由可得或,所以的取值范围是.
3.解:(1)的图像如图所示.
(2)由(1)知,的图像与轴交点的纵坐标为,且各部分所在直线斜率的最大值为,故当且仅当且时,在成立,因此的最小值为.
4.证明:由柯西不等式,得.
因为,所以,
当且仅当时,不等式取等号,此时,
所以的最小值为4.
相关文档
- 二年级数学上册第一单元100以内的2021-05-11 23:54:5913页
- 人教版六年级数学上册-教学计划案2021-05-11 23:54:424页
- 高考地理一轮复习冷热不均引起大气2021-05-11 23:54:4022页
- 基础练习02江苏高考英语3500词汇复2021-05-11 23:54:3210页
- 2012年台湾中考数学试卷2021-05-11 23:54:3218页
- 2020高考化学考前微专题突破练十一2021-05-11 23:53:3615页
- 五年级上册数学课件 第6单元《第12021-05-11 23:53:2725页
- 曲靖一中高考冲刺卷理科综合一2021-05-11 23:53:1913页
- 医学考试-结核病专业实践能力分类2021-05-11 23:53:1039页
- 高考数学难点突破22__轨迹方程的求2021-05-11 23:52:329页