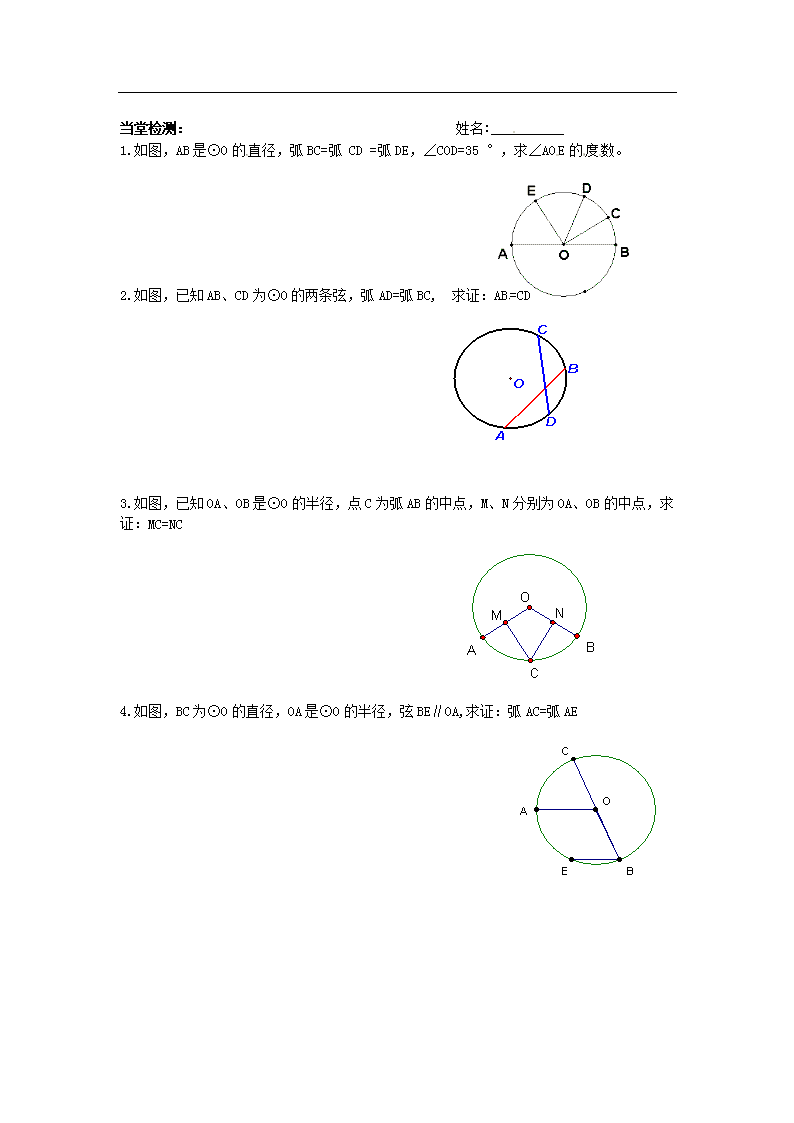九年级下册数学同步练习2-2-1 圆心角 湘教版 2页

‎2.2 圆心角、圆周角 ‎ ‎2.2.1 圆心角 学习目标：‎ 1、 了解圆心角的概念；‎ 2、 掌握在同圆或等圆中，圆心角、弦、弧之间的关系定理及该定理在解题中的应用．‎ 学习重点：圆心角、弧、弦之间关系定理并利用其解决相关问题．‎ 学习难点：圆心角、弧、弦之间关系定理中的“在同圆或等圆”条件的理解及定理的证明．‎ 学习过程：‎ ‎1.知识准备 ：‎ ‎（1）圆是轴   图形，任何一条    所在直线都是它的对称轴。‎ ‎（2）圆又是 对称图形，它的对称中心是 。‎ ‎（3）等圆概念：能够  的圆叫做等圆，同圆或等圆的半径 。‎ ‎2.自学探究：（自学教材内容，完成下列问题）‎ ‎（1）什么是圆心角?‎ ‎(2) 弧、弦、圆心角的关系： ‎ 定理：在同圆或等圆中，相等的圆心角所对的 相等，所对的 也  。‎ 同样，还可以得到： ‎ 在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角 ，所对的弦 。 ‎ 在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角 ，所对的弧 。‎ ‎（3）思考：‎ 定理“在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等”中，可否 把条件“在同圆或等圆中”去掉？为什么？ ‎ ‎ [来源:Zxxk.Com]‎ ‎3.学以致用 ‎（1）如图，AB，CD是⊙O的两条弦。‎ ‎⌒‎ ‎①如果AB=CD，那么 ， ‎ ‎⌒‎ ‎②如果AB=CD，那么 ， ‎ ‎③如果∠AOB=∠COD，那么 ， ‎ ‎④如果AB=CD,OMAB于M,ONCD于N。OM与ON 相等吗？为什么？‎ ‎(2) 如果两个圆心角相等，那么（    ）   ‎ ‎ A．这两个圆心角所对的弦相等      B．这两个圆心角所对的弧相等   ‎ ‎ C．这两个圆心角所对的弦的弦心距相等      D．以上说法都不对 当堂检测： 姓名: ‎ ‎[来源:学科网]‎ ‎1.如图，AB是⊙O的直径，弧BC=弧 CD =弧DE，∠COD=35 °，求∠AOE的度数。‎ ‎[来源:Zxxk.Com]‎ ‎2.如图，已知AB、CD为⊙O的两条弦，弧AD=弧BC, 求证：AB=CD ‎[来源:学|科|网]‎ ‎3.如图，已知OA、OB是⊙O的半径，点C为弧AB的中点，M、N分别为OA、OB的中点，求证：MC=NC ‎ ‎ ‎4.如图，BC为⊙O的直径，OA是⊙O的半径，弦BE∥OA,求证：弧AC=弧AE[来源:学*科*网]‎