2012年天津高考试题（文数解析版） 10页

‎ 2012年普通高等学校招生全国统一考试（天津卷）‎ 数学（文科）‎ ‎【整理】佛山市三水区华侨中学 骆方祥 ‎ 本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟。第Ⅰ卷1至2页，第Ⅱ卷3至5页。‎ ‎ 答卷前，考生务必将自己的姓名、准考证号填写在答题卡上，并在规定位置粘贴考试用条形码。答卷时，考生务必将答案涂写在答题卡上，答在试卷上的无效。考试结束后，将本试卷和答题卡一并交回。‎ ‎ 祝各位考生考试顺利！‎ ‎ 第Ⅰ卷 注意事项：‎ ‎ 1. 每小题选出答案后，用铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。‎ ‎ 2. 本卷共8小题，每小题5分，共40分。‎ 参考公式：‎ ‎﹒如果事件A,B胡斥，那么P(AUB)=P(A)+P(B).‎ ‎﹒棱柱的体积公式V=Sh.‎ 其中S表示棱柱的底面面积，h表示棱柱的高。‎ ‎﹒圆锥的体积公式V=Sh[来源:Zxxk.Com]‎ 其中S表示圆锥的底面面积，‎ H表示圆锥的高。[来源:学科网]‎ 一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的。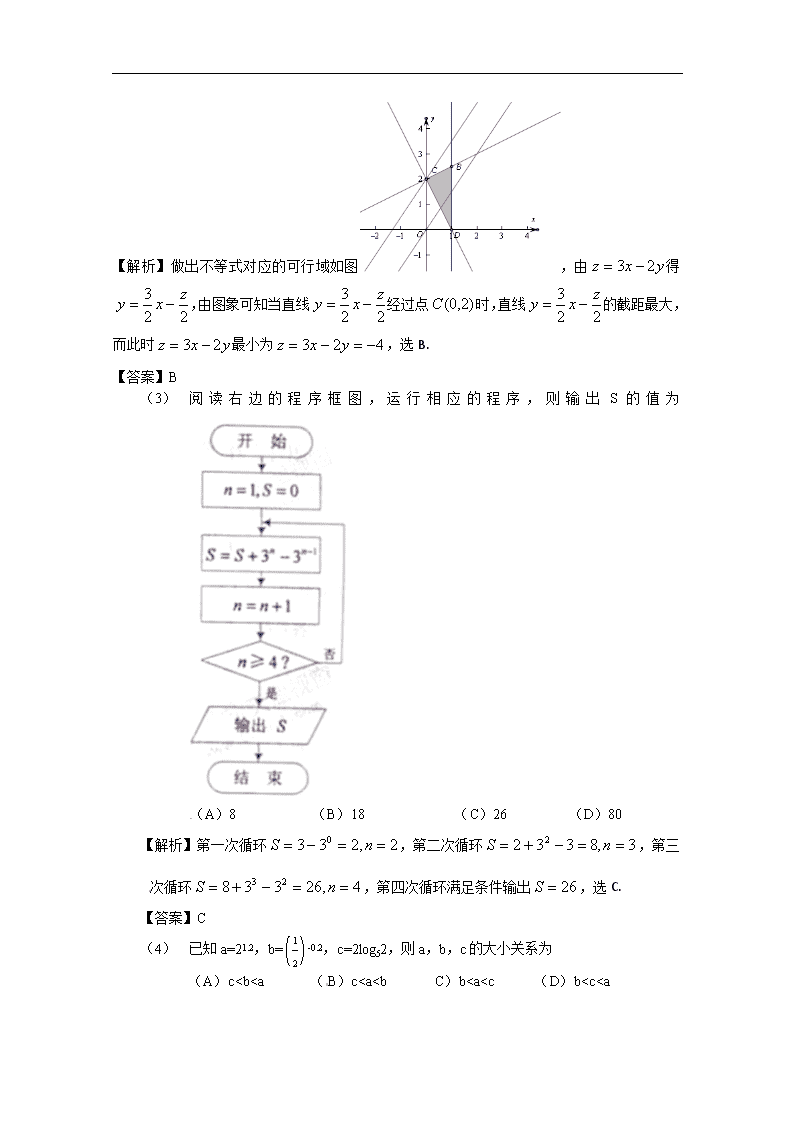‎ （1） i是虚数单位，复数=‎ ‎（A）1-i （B）-1+I ‎ ‎（C）1+I （D）-1-i ‎【解析】复数，选C.‎ ‎【答案】C ‎ ‎ （2） 设变量x,y满足约束条件,则目标函数z=3x-2y的最小值为 ‎ （A）-5 （B）-4 （C）-2 （D）3‎ ‎【解析】做出不等式对应的可行域如图，由得，由图象可知当直线经过点时，直线的截距最大，而此时最小为，选B.‎ ‎【答案】B （1） 阅读右边的程序框图，运行相应的程序，则输出S的值为 ‎（A）8 （B）18 （C）26 （D）80‎ ‎【解析】第一次循环，第二次循环，第三次循环，第四次循环满足条件输出，选C.‎ ‎【答案】C （2） 已知a=21.2，b=-0.2，c=2log52，则a，b，c的大小关系为 ‎（A）c”是“2x2+x-1>‎0”‎的 （A） 充分而不必要条件 （B） 必要而不充分条件 （C） 充分必要条件 （D） 既不充分也不必要条件 ‎【解析】不等式的解集为或，所以“”是“”成立的充分不必要条件，选A.‎ ‎【答案】A （2） 下列函数中，既是偶函数，又在区间（1,2）内是增函数的为 （A） y=cos2x，xR （B） y=log2|x|，xR且x≠0‎ （C） y=，xR （D） y=x3+1，xR ‎【解析】函数为偶函数，且当时，函数为增函数，所以在上也为增函数，选B.‎ ‎【答案】B （3） 将函数f(x)=sin（其中>0）的图像向右平移个单位长度，所得图像经过点（，0），则的最小值是 ‎（A） （B）1 C） （D）2‎ ‎【解析】函数向右平移得到函数，因为此时函数过点，所以，即所以,所以的最小值为2，选D.‎ ‎【答案】D （4） 在△ABC中， A=90°，AB=1，设点P，Q满足=， =(1-)， R。若=-2，则=‎ ‎（A） （B） C） （D）2‎ ‎【解析】如图，设 ，则，又，，由得，即，选B.‎ ‎【答案】B 第Ⅱ卷 注意事项：‎ ‎1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。[来源:Zxxk.Com]‎ ‎2.本卷共12小题，共110分。‎ 二.填空题：本答题共6小题，每小题5分，共30分。‎ ‎（9）集合中最小整数位 .‎ ‎【解析】不等式，即，，所以集合，所以最小的整数为。‎ ‎【答案】‎ ‎（10）一个几何体的三视图如图所示（单位：m）,则该几何体的体积 .‎ ‎ ‎ ‎【解析】由三视图可知这是一个下面是个长方体，上面是个平躺着的五棱柱构成的组合体。长方体的体积为，五棱柱的体积是，所以几何体的总体积为。‎ ‎【答案】‎ ‎（11）已知双曲线与双曲线有相同的渐近线，且的右焦点为,则 ‎ ‎【解析】双曲线的渐近线为，而的渐近线为，所以有，，又双曲线的右焦点为，所以，又，即，所以。‎ ‎【答案】1，2‎ ‎（12）设,若直线与轴相交于点A,与y轴相交于B，且l与圆相交所得弦的长为2，O为坐标原点，则面积的最小值为 。‎ ‎【解析】直线与两坐标轴的交点坐标为，直线与圆相交所得的弦长为2，圆心到直线的距离满足，所以，即圆心到直线的距离，所以。三角形的面积为，又，当且仅当时取等号，所以最小值为。‎ ‎【答案】3‎ ‎（13）如图，已知和是圆的两条弦，过点作圆的切线与的延长线相交于.过点作的平行线与圆交于点,与相交于点,,,,则线段的长为 .‎ ‎【解析】如图连结BC，BE，则∠1=∠2，∠2=∠A ‎，又∠B=∠B，∽，,代入数值得BC=2，AC=4，又由平行线等分线段定理得,解得CD=.‎ ‎【答案】‎ ‎（14）已知函数的图像与函数的图像恰有两个交点，则实数的取值范围是 .‎ ‎【解析】函数，当时，，当时，，综上函数，做出函数的图象，要使函数与 有两个不同的交点，则直线必须在蓝色或黄色区域内，如图，则此时当直线经过黄色区域时，满足，当经过蓝色区域时，满足，综上实数的取值范围是或。‎ ‎【答案】或。‎ 三.解答题：本大题共6小题，共80分。解答应写出文字说明，证明过程或演算步骤。（15题）（本小题满分13分）‎ 某地区有小学21所，中学14所，大学7所，现采取分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查。‎ ‎（I）求应从小学、中学、大学中分别抽取的学校数目。‎ ‎（II）若从抽取的6所学校中随机抽取2所学校做进一步数据分析，‎ ‎ （1）列出所有可能的抽取结果；‎ ‎（2）求抽取的2所学校均为小学的概率。‎ ‎【解析】（1）从小学、中学、大学中分别抽取的学校数目之比为 ‎ 得：从小学、中学、大学中分别抽取的学校数目为 ‎ （2）（i）设抽取的6所学校中小学为，中学为，大学为；‎ ‎ 抽取2所学校的结果为：，‎ ‎ 共种；‎ ‎ （ii）抽取的2所学校均为小学的结果为：共种 ‎ 抽取的2所学校均为小学的概率为 ‎（16）（本小题满分13分）‎ ‎ 在中，内角所对的分别是；已知；‎ ‎（I）求和的值； （II）求的值。‎ ‎【解析】（I）‎ ‎ ‎ ‎ ‎ ‎ （II）‎ ‎ ‎ ‎17.（本小题满分13分）‎ 如图，在四棱锥中，底面是矩形，‎ ‎（I）求异面直线与所成角的正切值；‎ ‎（II）证明：平面平面；‎ ‎（III）求直线与平面所成角的正弦值。‎ ‎【解析】（I）是与所成角 ‎ 在中，‎ ‎ ‎ ‎ 异面直线与所成角的正切值为 ‎（II）面 ‎ 面 平面平面 ‎（III）过点作于点，连接 ‎ 平面平面面是直线与平面所成角 ‎ ‎ ‎ 在中，‎ ‎ 在中，‎ ‎ 得：直线与平面所成角的正弦值为 ‎（18）（本题满分13分）‎ 已知是等差数列，其前项和为，是等比数列，‎ ‎ ，.‎ ‎(Ⅰ)求数列{}与{}的通项公式；‎ ‎ (Ⅱ)记；证明：‎ ‎【解析】(Ⅰ)设数列的公差为，数列的公比为；‎ 则 ‎ ‎ 得：‎ ‎(Ⅱ)‎ ‎ ‎ ‎ 当时，‎ ‎（19）（本小题满分14分）已知椭圆，点在椭圆上；‎ ‎（I）求椭圆的离心率；‎ ‎（II）设为椭圆的右顶点，为坐标原点，若在椭圆上且满足求直线 的斜率的值。‎ ‎【解析】(Ⅰ) 点在椭圆上 ‎ (Ⅱ) 设；则 ‎ ‎ ‎ 直线的斜率 ‎（20）（本小题满分14分）‎ 已知函数 ‎（I）求函数的单调区间；‎ ‎（II）若函数在区间内恰有两个零点，求的取值范围；‎ ‎（III）当时，设函数在区间上的最大值为，最小值为，‎ 记；求函数在区间上的最小值。‎ ‎【解析】(Ⅰ) ‎ ‎ 或，‎ ‎ 得：函数的单调递增区间为，单调递减区间为 ‎(Ⅱ) 函数在内单调递增，在内单调递减 ‎ 原命题（lfxlby）‎ ‎（III）当时，‎ 在上单调递增,在上单调递减 当 ‎ ‎ 当 ‎ ‎ 得：函数在区间上的最小值为（lfxlby）‎