- 1.48 MB
- 2021-05-10 发布
-1-
基础夯实 自我诊断
解答动力学综合问题的三大基本观点
1.解动力学问题的三个基本观点
-2-
基础夯实 自我诊断
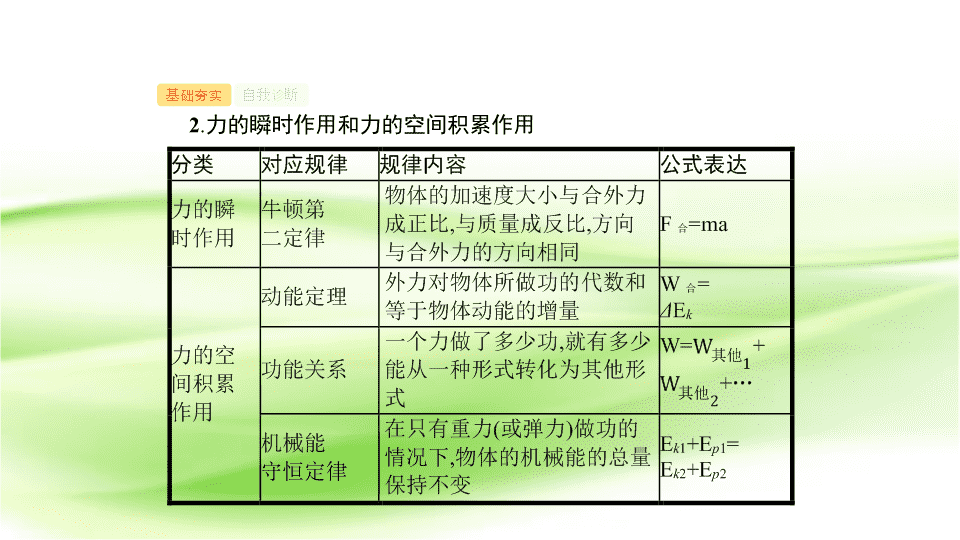
2.力的瞬时作用和力的空间积累作用
-3-
基础夯实 自我诊断
3.利用动量和能量的观点解题的技巧
(1)若研究对象为一个系统,应优先考虑应用动量守恒定律和能量
守恒定律(机械能守恒定律)。
(2)若研究对象为单一物体,且涉及功和位移问题时,应优先考虑
动能定理。
(3)因为动量守恒定律、能量守恒定律(机械能守恒定律)、动能
定理都只考查一个物理过程的始末两个状态有关物理量间的关系,
对过程的细节不予细究,这正是它们的方便之处。特别对于变力做
功问题,就更显示出它们的优越性。
-4-
基础夯实 自我诊断
1.一质量为2 kg的物体受水平拉力F作用,在粗糙水平面上做加速
直线运动时的a-t图像如图所示,t=0时其速度大小为2 m/s,滑动摩擦
力大小恒为2 N,则( )
A.t=6 s时,物体的速度为18 m/s
B.在0~6 s内,合力对物体做的功为400 J
C.在0~6 s内,拉力对物体的冲量为36 N·s
D.t=6 s时,拉力F的功率为200 W
答案解析解析
关闭
答案解析
关闭
-5-
基础夯实 自我诊断
2.如图所示,水平光滑轨道AB与竖直半圆形光滑轨道在B点平滑
连接,AB段长x=10 m,半圆形轨道半径R=2.5 m。质量m=0.10 kg的
小滑块(可视为质点)在水平恒力F作用下,从A点由静止开始运动,
经B点时撤去力F,小滑块进入半圆形轨道,沿轨道运动到最高点C,
从C点水平飞出。重力加速度g取10 m/s2。
(1)若小滑块从C点水平飞出后又恰好落在A点。求:
①滑块通过C点时的速度大小;
②滑块刚进入半圆形轨道时,在B点对轨道压力的大小。
(2)如果要使小滑块能够通过C点,求水平恒力F应满足的条件。
-6-
基础夯实 自我诊断
解析: (1)①设滑块从C点飞出时的速度为vC,从C点运动到A点
时间为t,滑块从C点飞出后,做平抛运动。
竖直方向:2R= gt2
水平方向:x=vCt
解得vC=10 m/s。
②设滑块通过B点时的速度为vB,根据机械能守恒定律得
设滑块在B点受轨道的支持力为FN,根据牛顿第二定律得
联立解得FN=9 N,根据牛顿第三定律,滑块在B点对轨道的压力
FN'=FN=9 N。
-7-
基础夯实 自我诊断
(2)若滑块恰好能够经过C点,设此时滑块的速度为vC',
滑块由A点运动到C点的过程中,由动能定理得
解得水平恒力F应满足的条件为F≥0.625 N。
答案: (1)①10 m/s ②9 N (2)F≥0.625 N
-8-
基础夯实 自我诊断
3.如图所示,一质量为m2的小车支架上用细线悬挂着一质量为m3
的小球停在光滑水平面上。另一质量为m1的小车以速度v0向m2撞
来,并立即与它粘连在一起。求小球m3能向上摆起的最大高度。
答案解析解析
关闭
答案解析
关闭
-9-
考点一 考点二 考点三
动力学方法的应用(师生共研)
若一个物体参与了多个运动过程,而运动过程只涉及运动和力的
问题或只要求分析物体的动力学特点而不涉及能量问题,则常常用
牛顿运动定律、运动学规律和动量定理等求解。
-10-
考点一 考点二 考点三
例1(2018·宁夏银川质检)质量为m1=1 200 kg的汽车A以速度
v1=21 m/s沿平直公路行驶时,驾驶员发现前方不远处有一质量
m2=800 kg的汽车B以速度v2=15 m/s迎面驶来,两车立即同时急刹车,
使车做匀减速运动,但两车仍在开始刹车t=1 s后猛烈地相撞,相撞
后结合在一起再滑行一段距离后停下,设两车与路面间的动摩擦因
数μ=0.3,g取10 m/s2,忽略碰撞过程中路面摩擦力的冲量,求:
(1)两车碰撞后刚结合在一起时的速度大小;
(2)设两车相撞时间(从接触到一起滑行)t0=0.2 s,则A车受到的水
平平均冲力是其自身重力的几倍;
(3)两车一起滑行的距离。
-11-
考点一 考点二 考点三
解析:(1)对减速过程有a=μg,
对A车有vA=v1-at,
对B车有vB=v2-at,
以碰撞前A车运动的方向为正方向,对碰撞过程由动量守恒定律
得m1vA-m2vB=(m1+m2)v共,
解得v共=6 m/s。
(2)对A车由动量定理得,-Ft0=m1v共-m1vA,
解得F=7.2×104 N。
解得x=6 m。
答案:(1)6 m/s (2)6倍 (3)6 m
-12-
考点一 考点二 考点三
例2如图所示,一质量为m的物块在与水平方向成θ的力F的作用
下从A点由静止开始沿水平直轨道运动,到B点后撤去力F,物体飞出
后越过“壕沟”落在平台EG段。已知物块的质量m=1 kg,物块与水
平直轨道间的动摩擦因数μ=0.5,AB段长L=10 m,B、E两点的高度
差h=0.8 m,B、E两点的水平距离x=1.6 m。若物块可看作质点,空气
阻力不计,g取10 m/s2。
-13-
考点一 考点二 考点三
(1)为使物块越过“壕沟”,求物块在B点最小速度v的大小;
(2)若θ=37°,为使物块恰好越过“壕沟”,求拉力F的大小;(sin
37°=0.6,cos 37°=0.8)
(3)若θ大小不确定,为使物块恰好越过“壕沟”,求力F的最小值。
(结果可保留根号)
答案解析解析
关闭
答案解析
关闭
-14-
考点一 考点二 考点三
突破训练
1.(2018·山西五校四联)如图甲所示,质量均为m=0.5 kg的相同物
块P和Q(可视为质点)分别静止在水平地面上A、C两点。P在按图
乙所示随时间变化的水平力F作用下由静止开始向右运动,3 s末撤
去力F,此时P运动到B点,之后继续滑行并与Q发生弹性碰撞。已知
B、C两点间的距离l=3.75 m,P、Q与地面间的动摩擦因数均为
μ=0.2,g取10 m/s2,求P到达B点时的速度大小v及其与Q碰撞前瞬间
的速度大小v1。
-15-
考点一 考点二 考点三
解析:在0~3 s内,以向右为正方向,对P由动量定理有
F1t1+F2t2-μmg(t1+t2)=mv-0,
其中F1=2 N,F2=3 N,t1=2 s,t2=1 s,
解得v=8 m/s,
设P在B、C两点间滑行的加速度大小为a,由牛顿第二定律有
μmg=ma,
解得v1=7 m/s。
答案:8 m/s 7 m/s
-16-
考点一 考点二 考点三
能量观点的应用(师生共研)
若一个物体参与了多个运动过程,若该过程涉及能量转化问题,
并且具有功能关系的特点,则往往用动能定理、机械能守恒定律或
能量守恒定律求解。
-17-
考点一 考点二 考点三
例3如图所示,一物体质量m=2 kg,在倾角θ=37°的斜面上的A点以
初速度v0=3 m/s下滑,A点距弹簧上端B的距离AB=4 m。当物体到
达B点后又将弹簧压缩到C点,最大压缩量BC=0.2 m,然后物体又被
弹簧弹回,弹到的最高位置D点,D点距A点的距离AD=3 m。挡板及
弹簧质量不计,g取10 m/s2,sin 37°=0.6。求:
(1)物体与斜面间的动摩擦因数μ;
(2)弹簧的最大弹性势能Epm。
答案解析解析
关闭
答案解析
关闭
-18-
考点一 考点二 考点三
解题探究①物体从开始位置A点到最后D点的过程中,弹性势能
没有 (选填“有”或“没有”)发生变化;利用公式Q=Ff·x计算摩擦生
热时,x表示物体经过的路程 。
②物体到达C点时,原来在A点的动能和重力势能转化成了何种
能量?
提示:弹性势能和内能。
-19-
考点一 考点二 考点三
例4(多选)如图所示,轻质弹簧一端固定,另一端与一质量为m、套
在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长。若圆环
从A处由静止开始下滑,则其经过B处的速度最大,到达C处的速度
为零,AC=h。若圆环在C处获得一竖直向上的初速度v,则恰好能回
到A。弹簧始终在弹性限度内。则圆环( )
A.下滑过程中,加速度一直减小
D.上滑经过B的速度大于下滑经过B的速度
答案解析解析
关闭
答案解析
关闭
-20-
考点一 考点二 考点三
力学三大观点的综合应用(师生共研)
这类模型各阶段的运动过程具有独立性,只要对不同过程分别选
用相应规律即可,两个相邻的过程连接点的速度是联系两过程的纽
带。
-21-
考点一 考点二 考点三
例5如图所示,一条带有圆轨道的长轨道水平固定,圆轨道竖直,底
端分别与两侧的直轨道相切,半径R=0.5 m,物块A以v0=6 m/s的速度
滑入圆轨道,滑过最高点Q,再沿圆轨道滑出后,与直轨道上P处静止
的物块B碰撞,碰后粘在一起运动,P点左侧轨道光滑,右侧轨道呈粗
糙段、光滑段交替排列,每段长度都为l=0.1 m,物块与各粗糙段间
的动摩擦因数都为μ=0.1,A、B的质量均为m=1 kg(重力加速度g取
10 m/s2;A、B视为质点,碰撞时间极短)。
-22-
考点一 考点二 考点三
(1)求A滑过Q点时的速度大小v和受到的弹力大小F;
(2)若碰后AB最终停止在第k个粗糙段上,求k的数值;
(3)求碰后AB滑至第n个(n