2020高考文科数学二轮分层特训卷：模拟仿真专练（四） 15页

专练(四) 一、选择题(本大题共 12 小题，每小题 5 分，共 60 分．在 每小题给出的四个选项中，只有一项是符合题目要求的) 1．[2019·广东深圳高级中学期末]已知集合 A＝{x∈Z|－ 1≤x≤4}，B＝{－2，－1,4,8,9}，设 C＝A∩B，则集合 C 的元素 个数为( ) A．9 B．8 C．3 D．2 答案：D 解析：A＝{x∈Z|－1≤x≤4}＝{－1,0,1,2,3,4}，B＝{－2，－ 1,4,8,9}，则 C＝A∩B＝{－1,4}，集合 C 的元素个数为 2，故选 D. 2．[2019·福建晋江四校联考]复数 z＝a＋i(a∈R)的共轭复数 为 z ，满足| z |＝1，则复数 z＝( ) A．2＋i B．2－i C．1＋i D．i 答案：D 解析：根据题意可得 z ＝a－i，所以| z |＝ a2＋1＝1，解得 a＝0，所以复数 z＝i.故选 D. 3．[2019·重庆一中月考]设 a，b，c 是平面向量，则 a·b＝b·c 是 a＝c 的( ) A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 答案：B 解析：由 a·b＝b·c 得(a－c)·b＝0，∴a＝c 或 b＝0 或(a－ c)⊥b，∴a·b＝b·c 是 a＝c 的必要不充分条件．故选 B. 4．[2019·黑龙江牡丹江一中月考]关于函数 f(x)＝sin 2x＋π 4 与函数 g(x)＝cos 2x－3π 4 ，下列说法正确的是( ) A．函数 f(x)和 g(x)的图象有一个交点在 y 轴上 B．函数 f(x)和 g(x)的图象在区间(0，π)内有 3 个交点 C．函数 f(x)和 g(x)的图象关于直线 x＝π 2 对称 D．函数 f(x)和 g(x)的图象关于原点(0,0)对称 答案：D 解 析 ： ∵g( － x) ＝ cos －2x－3π 4 ＝ cos 2x＋3π 4 ＝ cos 2x＋π 4 ＋π 2 ＝－sin 2x＋π 4 ，∴g(－x)＝－f(x)，∴函数 f(x)和 g(x) 的图象关于原点(0,0)对称，故选 D. 5．[2019·湖北武汉武昌调研考]已知数列{an}的前 n 项和 Sn ＝n2－1，则 a1＋a3＋a5＋a7＋a9＝( ) A．40 B．44 C．45 D．49 答案：B 解析：解法一 因为 Sn＝n2－1，所以当 n≥2 时，an＝Sn－ Sn － 1＝n2－1－(n－1)2＋1＝2n－1，又 a1＝S1＝0，所以 an＝ 0，n＝1， 2n－1，n≥2， 所以 a1＋a3＋a5＋a7＋a9＝0＋5＋9＋13＋17 ＝44.故选 B. 解法二 因为 Sn＝n2－1，所以当 n≥2 时，an＝Sn－Sn－1＝ n2 － 1 － (n － 1)2 ＋ 1 ＝ 2n － 1 ， 又 a1 ＝ S1 ＝ 0 ， 所 以 an ＝ 0，n＝1， 2n－1，n≥2， 所以{an}从第二项起是等差数列，a2＝3，公差 d＝2，所以 a1＋a3＋a5＋a7＋a9＝0＋4a6＝4×(2×6－1)＝44.故选 B. 6．[2019·黑龙江哈尔滨四校联考]已知函数 f(x)＝cosπx 3 ，执 行如图所示的程序框图，则输出的 S 值为( ) A．670 B．6701 2 C．671 D．672 答案：C 解析：执行程序框图，y＝f(1)＝cosπ 3 ＝1 2 ，S＝0＋1 2 ＝1 2 ，n＝ 1＋1＝2；y＝f(2)＝cos2π 3 ＝－1 2 ，S＝1 2 ，n＝2＋1＝3；y＝f(3)＝cos π＝－1，S＝1 2 ，n＝3＋1＝4；y＝f(4)＝cos4π 3 ＝－1 2 ，S＝1 2 ，n＝4 ＋1＝5；y＝f(5)＝cos5π 3 ＝1 2 ，S＝1 2 ＋1 2 ＝1，n＝6；y＝f(6)＝cos2π ＝1，S＝1＋1＝2，n＝7……直到 n＝2 016 时，退出循环．∵函 数 y＝cos nπ 3 是以 6 为周期的周期函数，2 015＝6×335＋5，f(2 016) ＝cos 336π＝cos(2π×138)＝1，∴输出的 S＝336×2－1＝671.故 选 C. 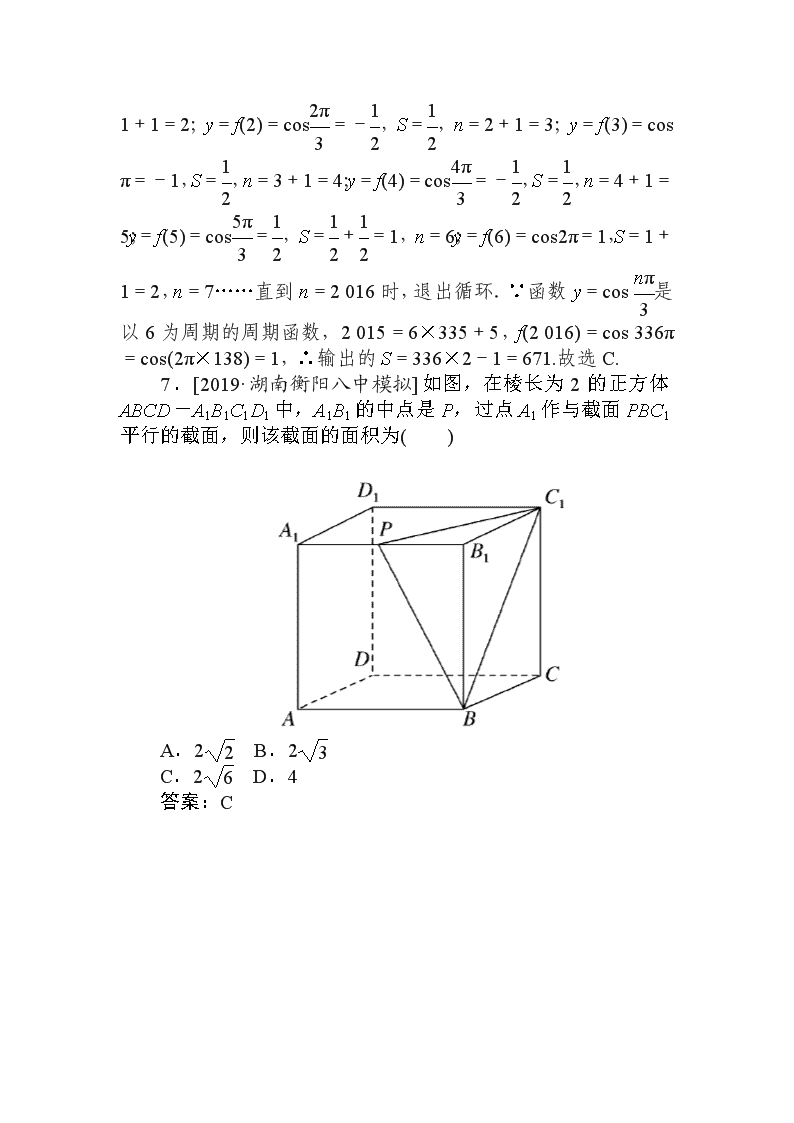7．[2019·湖南衡阳八中模拟]如图，在棱长为 2 的正方体 ABCD－A1B1C1D1 中，A1B1 的中点是 P，过点 A1 作与截面 PBC1 平行的截面，则该截面的面积为( ) A．2 2 B．2 3 C．2 6 D．4 答案：C 解析：易知截面是菱形，如图，分别取棱 D1C1，AB 的中点 E，F，连接 A1E，A1F，CF，CE，则菱形 A1ECF 为符合题意的 截面． 连接 EF，A1C，易知 EF＝2 2，A1C＝2 3，EF⊥A1C，所 以截面的面积 S＝1 2EF·A1C＝2 6.故选 C. 8．[2019·河北张家口期中]已知 x>0，y>0，lg 2x＋lg 8y＝lg 2， 则1 x ＋ 1 3y 的最小值是( ) A．1 B．2 C．2 3 D．4 答案：D 解析：通解 ∵lg 2x＋lg 8y＝lg 2，∴lg 2x＋3y＝lg 2，∴x＋3y ＝1.又 x>0，y>0，∴1 x ＋ 1 3y ＝ 1 x ＋ 1 3y (x＋3y)＝2＋3y x ＋ x 3y ≥2＋2 ＝4，当且仅当 x＝1 2 ，y＝1 6 时等号成立，所以1 x ＋ 1 3y 的最小值是 4. 故选 D. 优解 ∵lg 2x＋lg 8y＝lg 2，∴lg 2x＋3y＝lg 2，∴x＋3y＝1.又 x>0，y>0，∴1 x ＋ 1 3y ＝x＋3y 3xy ＝ 1 3xy ≥ 1 x＋3y 2 2 ＝4，当且仅当 x＝1 2 ， y＝1 6 时等号成立，所以1 x ＋ 1 3y 的最小值是 4，故选 D. 9．[2019·河北唐山摸底]已知函数 f(x)＝sin x－sin 3x， x∈[0,2π]，则 f(x)的所有零点之和等于( ) A．5π B．6π C．7π D．8π 答案：C 解析：f(x)＝sin x－sin(2x＋x)＝sin x－sin 2xcos x－cos 2xsin x ＝sin x－2sin x(1－sin2x)－(1－2sin2x)sin x＝sin x－(3sin x－ 4sin3x)＝2sin x(2sin2x－1)， 令 f(x)＝0 得 sin x＝0 或 sin x＝± 2 2 . 于是，f(x)在[0,2π]上的所有零点为 x＝0，π 4 ，3π 4 ，π，5π 4 ，7π 4 ，2π. 故 f(x)的所有零点之和为 0＋π 4 ＋3π 4 ＋π＋5π 4 ＋7π 4 ＋2π＝7π， 故选 C. 10．[2019·江西七校联考]图中的图案是我国古代建筑中的一 种装饰图案，形若铜钱，寓意富贵吉祥，在圆内随机取一点，则 该点取自阴影区域(由四条半径与大圆半径相等的四分之一圆弧 围成)内的概率是( ) A.1 2 B.1 3 C.4 π －1 D．2－4 π 答案：C 解析：设圆的半径为 1，则该点取自阴影区域内的概率 P＝ S 阴影 S 圆 ＝2×2－π π ＝4 π －1，故选 C. 11．[2019·四川内江一模]设函数 f(x)在 R 上存在导数 f′(x)， 对任意的 x∈R，有 f(－x)－f(x)＝0，且 x∈[0，＋∞)时，f′(x)>2x， 若 f(a－2)－f(a)≥4－4a，则实数 a 的取值范围为( ) A．(－∞，1] B．[1，＋∞) C．(－∞，2] D．[2，＋∞) 答案：A 解析：对任意的 x∈R，有 f(－x)－f(x)＝0，所以 f(x)为偶函 数． 设 g(x)＝f(x)－x2，所以 g′(x)＝f′(x)－2x， 因为 x∈[0，＋∞)时 f′(x)>2x，所以 x∈[0，＋∞)时，g′(x) ＝f′(x)－2x>0，所以 g(x)在[0，＋∞)上为增函数． 因为 f(a－2)－f(a)≥4－4a，所以 f(a－2)－(a－2)2≥f(a)－a2， 所以 g(a－2)≥g(a)，易知 g(x)为偶函数，所以|a－2|≥|a|， 解得 a≤1，故选 A. 12．[2019·河北衡水中学五调]已知抛物线 C：y2＝2px(p>0) 的焦点为 F，过点 F 的直线 l 与抛物线 C 交于 A，B 两点，且直 线 l 与圆 x2－px＋y2－3 4p2＝0 交于 C，D 两点．若|AB|＝2|CD|， 则直线 l 的斜率为( ) A．± 2 2 B．± 3 2 C．±1 D．± 2 答案：C 解析：由题设可得圆的方程为 x－p 2 2＋y2＝p2，故圆心坐标 为 p 2 ，0 ，为抛物线 C 的焦点，所以|CD|＝2p，所以|AB|＝4p.设 直线 l：x＝ty＋p 2 ，代入 y2＝2px(p>0)，得 y2－2pty－p2＝0.设 A(x1， y1) ， B(x2 ， y2) ， 则 y1 ＋ y2 ＝ 2pt ， y1y2 ＝ － p2 ， 则 |AB| ＝ 1＋t24p2t2＋4p2＝2p(1＋t2)＝4p，所以 1＋t2＝2，解得 t＝±1， 故选 C. 二、填空题(本大题共 4 小题，每小题 5 分，共 20 分．将正 确答案填在题中的横线上．) 13．某学校举办科技节活动，有甲、乙、丙、丁四个团队参 加“智能机器人”项目比赛，该项目只设置一个一等奖，在评奖 结果揭晓前，小张、小王、小李、小赵四位同学对这四个参赛团 队获奖结果预测如下： 小张说：“甲团队获得一等奖．” 小王说：“甲或乙团队获得一等奖．” 小李说：“丁团队获得一等奖．” 小赵说：“乙、丙两个团队均未获得一等奖．” 若这四位同学中只有两位的预测结果是对的，则获得一等奖 的团队是________． 答案：丁 解析：①若获得一等奖的团队是甲团队，则小张、小王、小 赵的预测结果是对的，小李的预测结果是错的，与题设矛盾； ②若获得一等奖的团队是乙团队，则小王的预测结果是对 的，小张、小李、小赵的预测结果是错的，与题设矛盾； ③若获得一等奖的团队是丙团队，则四人的预测结果都是错 的，与题设矛盾； ④若获得一等奖的团队是丁团队，则小李、小赵的预测结果 是对的，小张、小王的预测结果是错的，与题设相符． 故获得一等奖的团队是丁． 14．[2019·江苏无锡模考]以双曲线x2 5 －y2 4 ＝1 的右焦点为焦 点的抛物线的标准方程是________． 答案：y2＝12x 解析：双曲线中，c＝ 5＋4＝3，所以右焦点坐标为(3,0)， 故抛物线的焦点坐标为(3,0)，所以p 2 ＝3，p＝6，抛物线的标准方 程为 y2＝12x. 15 ． [2019· 云 南 第 一 次 统 一 检 测 ] 已 知 函 数 f(x) ＝ 3x－2－5，x<3， －log2x＋1，x≥3， 若 f(m)＝－6，则 f(m－61)＝________. 答案：－4 解析：∵函数 f(x)＝ 3x－2－5，x<3， －log2x＋1，x≥3， f(m)＝－6，∴ 当 m<3 时，f(m)＝3m－2－5＝－6，无解；当 m≥3 时，f(m)＝－log2(m ＋1)＝－6，解得 m＝63， ∴f(m－61)＝f(2)＝32－2－5＝－4. 16．[2019·安徽定远中学月考]已知等差数列{an}满足 a3＝6， a4＝7，bn＝(an－3)·3n，则数列{bn}的前 n 项和 Tn＝________. 答案：2n－1×3n＋1＋3 4 解析：因为 a3＝6，a4＝7，所以 d＝1， 所以 a1＝4，an＝n＋3，bn＝(an－3)·3n＝n·3n， 所以 Tn＝1×31＋2×32＋3×33＋…＋n×3n ①， 3Tn＝1×32＋2×33＋3×34＋…＋n×3n＋1 ②， ①－②得－2Tn＝3＋32＋33＋…＋3n－n×3n＋1＝3－3n＋1 1－3 － n×3n＋1， 所以 Tn＝2n－1×3n＋1＋3 4 . 三、解答题(本大题共 6 小题，共 70 分．解答应写出文字说 明、证明过程或演算步骤．) 17．(12 分)[2019·华大新高考联盟教学质量测评]在△ABC 中，角 A，B，C 所对的边分别为 a，b，c，△ABC 的面积为 S， b＝4，accos B＝2 3 3 S. (1)若 a，b，c 成等差数列，试判断△ABC 的形状； (2)求 a＋c 的取值范围． 解析：(1)由已知得 accos B＝ 3 3 acsin B，得 tan B＝ 3， 因为 0b＝4，所以 40，求得 m> 2或 m<－ 2. 设 P(x1，y1)，Q(x2，y2)，则 y1＋y2＝4m，y1y2＝8. 由(*)得 kPN＋kQN＝ y1 x1－x0 ＋ y2 x2－x0 ＝y1x2－x0＋y2x1－x0 x1－x0x2－x0 ＝ 0， 所以 y1(x2－x0)＋y2(x1－x0) ＝0，即 y1x2＋y2x1－x0 (y1＋y2)＝ 0. 消去 x1，x2，得 1 4y1y22＋1 4y2y21－x0(y1＋y2)＝0， 即 1 4y1y2(y1＋y2)－x0(y1＋y2)＝0. 因为 y1＋y2≠0，所以 x0＝1 4y1y2＝2， 于是存在点 N(2,0)，使得∠QNM＋∠PNM＝π. 21．(12 分)[2019·陕西西安中学期中]已知函数 f(x)＝1 2x2＋(1 －x)ex，g(x)＝x－ln x－a ln x＋1 x ，a<1. (1)求函数 g(x)的单调区间； (2)若对任意 x1∈[－1,0]，总存在 x2∈[e,3]，使得 f(x1)>g(x2) 成立，求实数 a 的取值范围． 解析：(1)因为 g′(x)＝1－1 x －a 1 x －1 x2 ＝x2－a＋1x＋a x2 ＝ x－ax－1 x2 ，a<1，又注意到函数 g(x)的定义域为(0，＋∞)，所 以讨论如下． 当 00，解得 01，令 g′(x)<0， 解得 a0，解得 x>1，令 g′(x)<0，解得 0g(x2)成 立，等价于函数 f(x)在[－1,0]上的最小值大于函数 g(x)在[e,3]上 的最小值． 当 x∈[－1,0]时，因为 f′(x)＝x(1－ex)≤0，当且仅当 x＝0 时不等式取等号，所以 f(x)在[－1,0]上单调递减，所以 f(x)在[－ 1,0]上的最小值为 f(0)＝1. 由(1)可知，函数 g(x)在[e,3]上单调递增，所以 g(x)在[e,3]上 的最小值为 g(e)＝e－(a＋1)－a e. 所以 1>e－(a＋1)－a e ，即 a>e2－2e e＋1 . 又 a<1，故所求实数 a 的取值范围是 e2－2e e＋1 ，1 . 选考题(请考生在第 22、23 题中任选一题作答，多答、不答 按本选考题的首题进行评分．) 22．(10 分)[2019·山东济南质量评估][选修 4－4：坐标系与 参数方程] 在平面直角坐标系 xOy 中，以坐标原点 O 为极点，x 轴的正 半轴为极轴建立极坐标系，曲线 C 的极坐标方程为ρcos2θ＝sin θ， 直线 l 的参数方程为 x＝ 3 2 t， y＝a＋1 2t (t 为参数)，其中 a>0， 直线 l 与曲线 C 相交于 M，N 两点． (1)求曲线 C 的直角坐标方程； (2)若点 P(0，a)满足 1 |PM| ＋ 1 |PN| ＝4，求 a 的值． 解析：(1)由已知可知ρ2cos2θ＝ρsin θ， 由{x＝ρcos θ， y＝ρsin θ 得曲线 C 的直角坐标方程为 y＝ x2. (2)将直线l的参数方程 x＝ 3 2 t， y＝a＋1 2t (t为参数)代入 y＝x2，得 3 4t2－1 2t－a＝0，且Δ＝1 4 ＋3a>0. 设 M，N 对应的参数分别为 t1，t2，则 t1＋t2＝2 3 ，t1t2＝－4 3a， 所以 t1、t2 异号． 所以 1 |PM| ＋ 1 |PN| ＝|PM|＋|PN| |PM||PN| ＝|t1－t2| |t1t2| ＝ t1＋t22－4t1t2 |t1t2| ＝ 4 9 －4× －4 3a |－4 3a| ＝4， 化简得 64a2－12a－1＝0，解得 a＝1 4 或 a＝－ 1 16(舍)． 所以 a 的值为1 4. 23．(10 分)[2019·河南省郑州市检测卷][选修 4－5：不等式 选讲] 已知函数 f(x)＝|3x－2a|＋|2x－2|(a∈R)． (1)当 a＝1 2 时，解不等式 f(x)>6； (2)若对任意 x0∈R，不等式 f(x0)＋3x0>4＋|2x0－2|都成立， 求 a 的取值范围． 解析：(1)当 a＝1 2 时， 不等式 f(x)>6 可化为|3x－1|＋|2x－2|>6， 当 x<1 3 时，不等式即为 1－3x＋2－2x>6，∴x<－3 5 ； 当1 3 ≤x≤1 时，不等式即为 3x－1＋2－2x>6，无解； 当 x>1 时，不等式即为 3x－1＋2x－2>6，∴x>9 5. 综上所述，不等式的解集为 x|x<－3 5 或 x>9 5 . (2)不等式 f(x0)＋3x0>4＋|2x0－2|恒成立可化为|3x0－2a|＋ 3x0>4 恒成立， 令 g(x)＝|3x－2a|＋3x＝ 6x－2a，x≥2a 3 ， 2a，x<2a 3 ， ∴函数 g(x)的最小值为 2a， 根据题意可得 2a>4，即 a>2， 所以 a 的取值范围为(2，＋∞)．