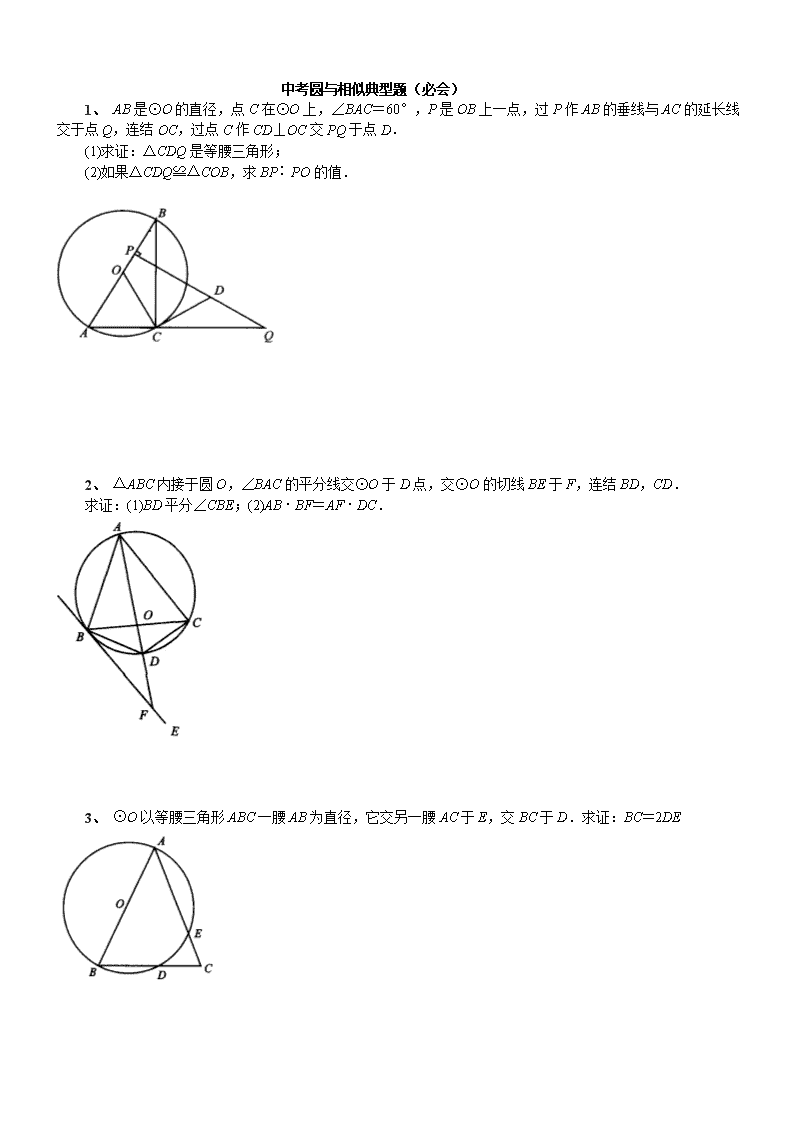中考相似圆练习题和答案必会 4页

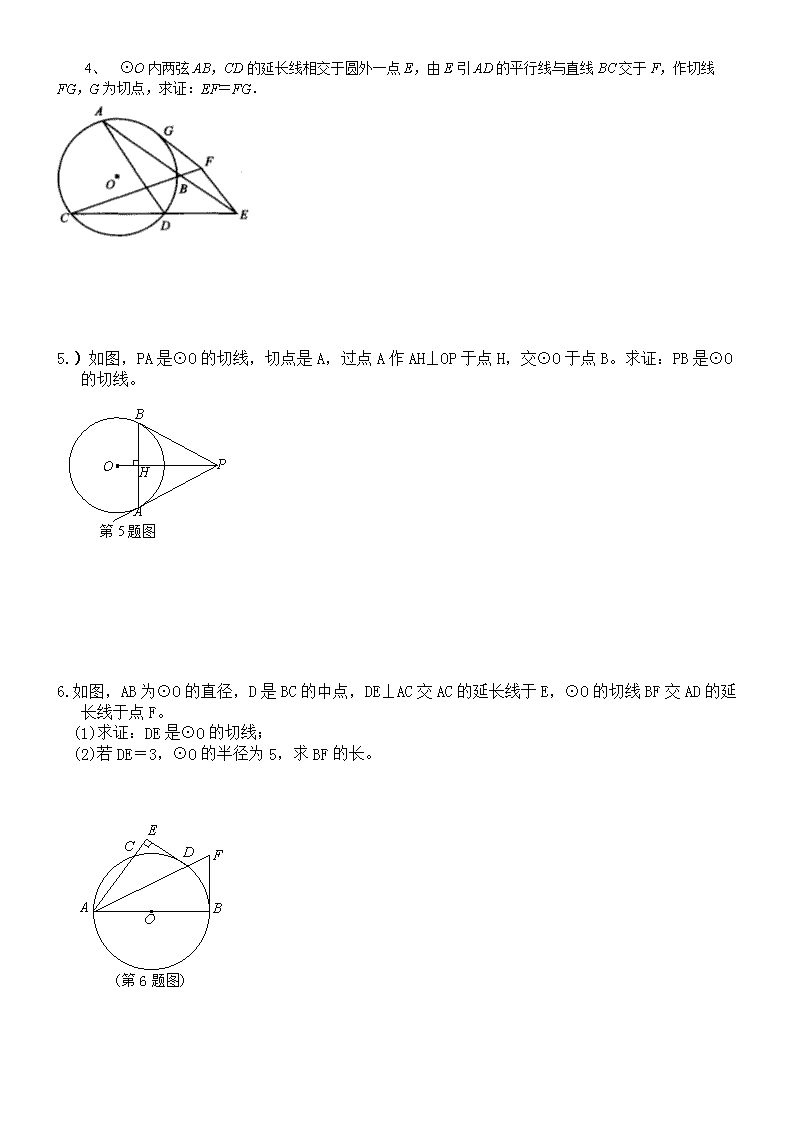
中考圆与相似典型题（必会）‎ ‎1、 AB是⊙O的直径，点C在⊙O上，∠BAC＝60°，P是OB上一点，过P作AB的垂线与AC的延长线交于点Q，连结OC，过点C作CD⊥OC交PQ于点D．‎ ‎(1)求证：△CDQ是等腰三角形；‎ ‎(2)如果△CDQ≌△COB，求BP∶PO的值．‎ ‎2、 △ABC内接于圆O，∠BAC的平分线交⊙O于D点，交⊙O的切线BE于F，连结BD，CD． ‎ 求证：(1)BD平分∠CBE；(2)AB·BF＝AF·DC．‎ ‎3、 ⊙O以等腰三角形ABC一腰AB为直径，它交另一腰AC于E，交BC于D．求证：BC＝2DE ‎4、 ⊙O内两弦AB，CD的延长线相交于圆外一点E，由E引AD的平行线与直线BC交于F，作切线FG，G为切点，求证：EF＝FG．‎ ‎5.）如图，PA是⊙O的切线，切点是A，过点A作AH⊥OP于点H，交⊙O于点B。求证：PB是⊙O的切线。‎ A B P O H 第5题图 ‎6.如图，AB为⊙O的直径，D是BC的中点，DE⊥AC交AC的延长线于E，⊙O的切线BF交AD的延长线于点F。‎ ‎(1)求证：DE是⊙O的切线；‎ ‎(2)若DE＝3，⊙O的半径为5，求BF的长。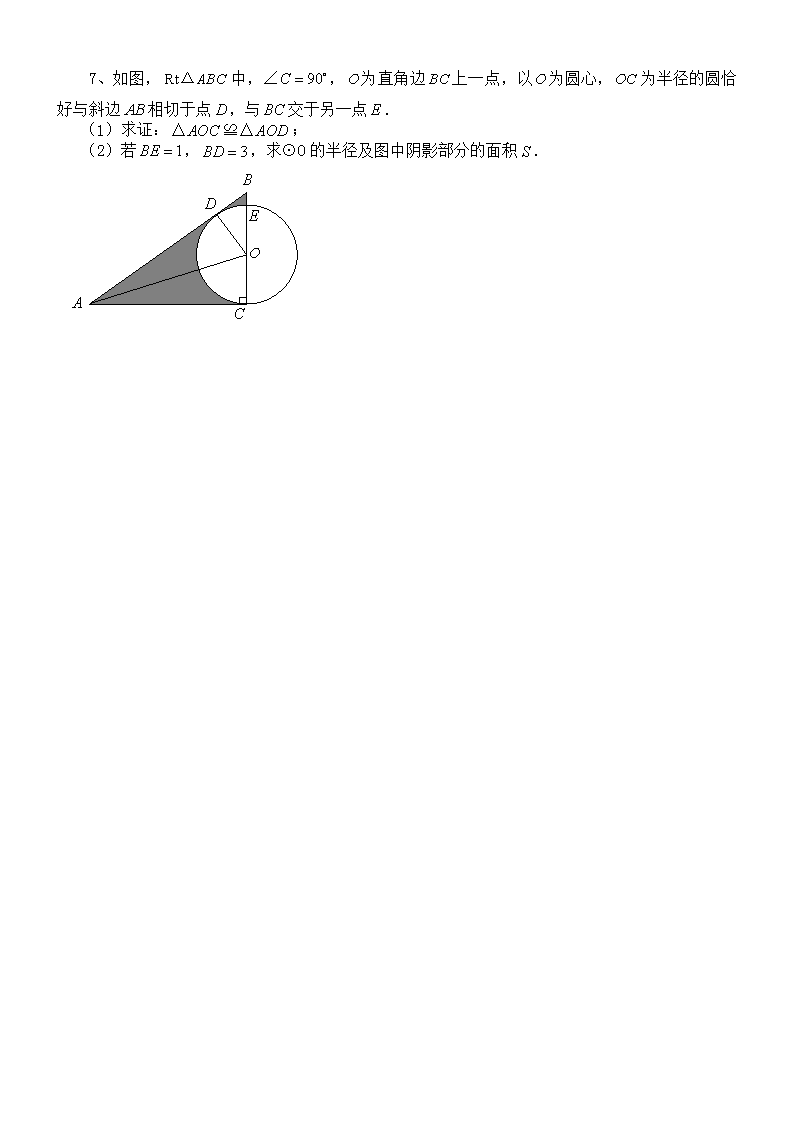‎ A B C D E F O ‎(第6题图)‎ ‎7、如图，中，，为直角边上一点，以为圆心，为半径的圆恰好与斜边相切于点，与交于另一点．‎ ‎（1）求证：；‎ ‎（2）若，，求⊙O的半径及图中阴影部分的面积．‎ 相似答案 ‎1、(1)证明：由已知得∠ACB＝90°，∠ABC＝30°，‎ ‎∴∠Q＝30°，∠BCO＝∠ABC＝30°．∵CD⊥OC，‎ ‎∴∠DCQ＝∠BCO＝30°，∴∠DCQ＝∠Q，‎ ‎∴△CDQ是等腰三角形．‎ ‎(2)解：设⊙O的半径为1，则AB＝2，OC＝1，‎ ‎∵等腰三角形CDQ与等腰三角形COB全等，∴CQ＝BC＝．‎ ‎∵，‎ ‎∴‎ ‎，‎ ‎∴．‎ ‎2、证明：(1)∵∠CAD＝∠BAD＝∠FBD，∠CAD＝∠CBD，‎ ‎∴∠CBD＝∠FBD，∴BD平分∠CBE．‎ ‎(2)在△DBF与△BAF中，‎ ‎∵∠FBD＝∠FAB，∠F＝∠F，∴△ABF∽△BDF，，∴AB·BF＝BD·AF．‎ 又∵BD＝CD，∴AB·BF＝CD·AF．‎ ‎3、证明：连结AD ∵AB是⊙O直径 ∴AD⊥BC ‎∵AB＝AC ∴BC＝2CD，∠B＝∠C ‎∵⊙O内接四边形ABDE ‎∴∠B＝∠DEC(四点共圆的一个内角等于对角的外角)‎ ‎∴∠C＝∠DEC ∴DE＝DC ‎∴BC＝2DE 证明：∵在△BFE与△EFC中有 ‎∠BEF＝∠A＝∠C，又 ∠BFE＝∠EFC，‎ ‎∴△BFE∽△EFC，，∴FE2＝FB·FC．‎ 又∵FG2＝FB·FC，∴FE2＝FG2，∴ FE＝FG．‎