2014年高考数学（文科）真题分类汇编I单元　统计 14页

数 学 I 单元 统计 I1 随机抽样 3．I1[2014·重庆卷] 某中学有高中生 3500 人，初中生 1500 人．为了解学生的学习情况， 用分层抽样的方法从该校学生中抽取一个容量为 n 的样本，已知从高中生中抽取 70 人，则 n 为( ) A．100 B．150 C．200 D．250 3．A [解析] 由题意，得 70 3500 ＝ n 3500＋1500 ，解得 n＝100. 11．I1[2014·湖北卷] 甲、乙两套设备生产的同类型产品共 4800 件，采用分层抽样的方 法从中抽取一个容量为 80 的样本进行质量检测．若样本中有 50 件产品由甲设备生产，则乙 设备生产的产品总数为________件． 11．1800 [解析] 设乙设备生产的产品总数为 n，则80－50 n ＝ 80 4800 ，解得 n＝1800. 3．I1[2014·湖南卷] 对一个容量为 N 的总体抽取容量为 n 的样本，当选取简单随机抽 样、系统抽样和分层抽样三种不同方法抽取样本时，总体中每个个体被抽中的概率分别为 p1，p2，p3，则( ) A．p1＝p2＜p3 B．p2＝p3＜p1 C．p1＝p3＜p2 D．p1＝p2＝p3 3．D [解析] 不管是简单随机抽样、系统抽样还是分层抽样，它们都是等概率抽样， 每个个体被抽中的概率均为n N. 2．I1、I2[2014·四川卷] 在“世界读书日”前夕，为了了解某地 5000 名居民某天的阅 读时间，从中抽取了 200 名居民的阅读时间进行统计分析．在这个问题中，5000 名居民的 阅读时间的全体是( ) A．总体 B．个体 C．样本的容量 D．从总体中抽取的一个样本 2．A [解析] 根据抽样统计的概念可知，统计分析的对象全体叫做“总体”．故选 A. 9．I1[2014·天津卷] 某大学为了解在校本科生对参加某项社会实践活动的意向，拟采用 分层抽样的方法，从该校四个年级的本科生中抽取一个容量为 300 的样本进行调查．已知该 校一年级、二年级、三年级、四年级的本科生人数之比为 4∶5∶5∶6，则应从一年级本科 生中抽取________名学生． 9．60 [解析] 由分层抽样方法可得，从一年级本科生中抽取的学生人数为 300× 4 4＋5＋5＋6 ＝60. 15．I1、K2[2014·天津卷] 某校夏令营有 3 名男同学 A，B，C 和 3 名女同学 X，Y，Z， 其年级情况如下表： 一年级 二年级 三年级 男同学 A B C 女同学 X Y Z 现从这 6 名同学中随机选出 2 人参加知识竞赛(每人被选到的可能性相同)． (1)用表中字母列举出所有可能的结果； (2)设 M 为事件“选出的 2 人来自不同年级且恰有 1 名男同学和 1 名女同学”，求事件 M 发生的概率． 15．解：(1)从 6 名同学中随机选出 2 人参加知识竞赛的所有可能结果为{A，B}，{A， C}，{A，X}，{A，Y}，{A，Z}，{B，C}，{B，X}，{B，Y}，{B，Z}，{C，X}，{C，Y}， {C，Z}，{X，Y}，{X，Z}，{Y，Z}，共 15 种． (2)选出的 2 人来自不同年级且恰有 1 名男同学和 1 名女同学的所有可能结果为{A，Y}， {A，Z}，{B，X}，{B，Z}，{C，X}，{C，Y}，共 6 种． 因此，事件 M 发生的概率 P(M)＝ 6 15 ＝2 5. I2 用样本估计总体 17．I2、I4[2014·安徽卷] 某高校共有学生 15 000 人，其中男生 10 500 人，女生 4500 人．为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集 300 位学生 每周平均体育运动时间的样本数据(单位：小时)． (1)应收集多少位女生的样本数据？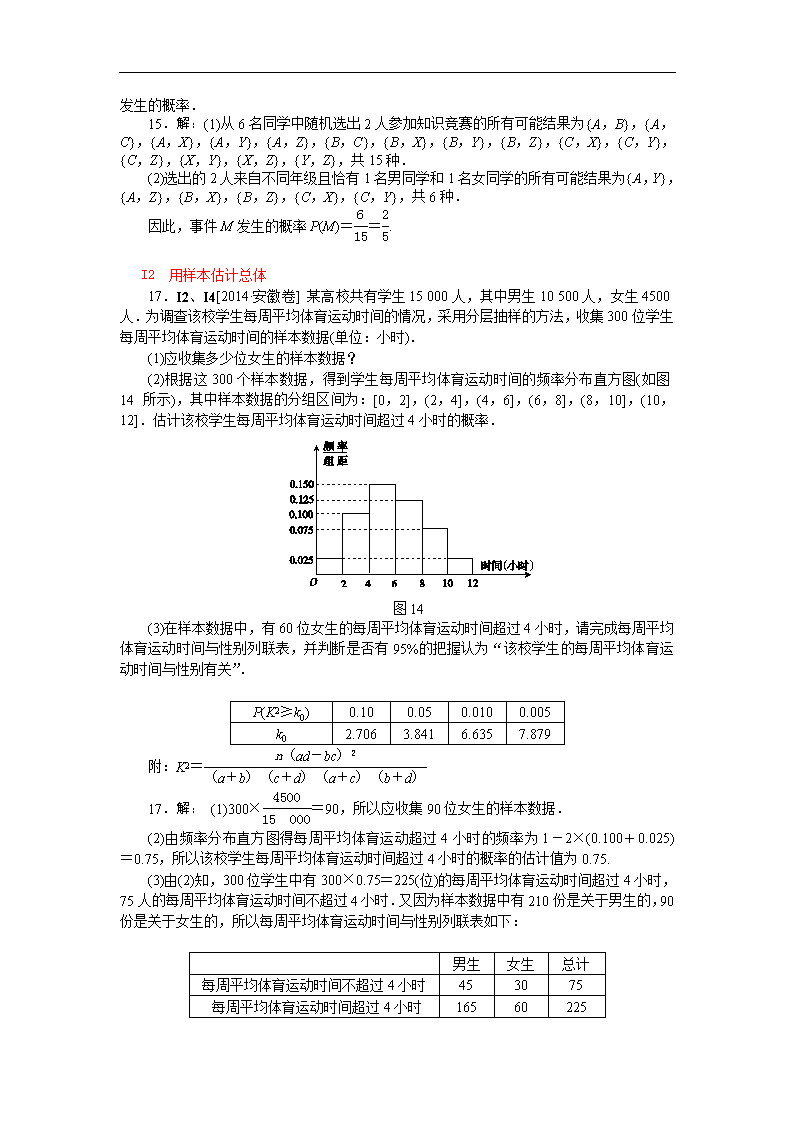 (2)根据这 300 个样本数据，得到学生每周平均体育运动时间的频率分布直方图(如图 14 所示)，其中样本数据的分组区间为：[0，2]，(2，4]，(4，6]，(6，8]，(8，10]，(10，12]．估 计该校学生每周平均体育运动时间超过 4 小时的概率． 图 14 (3)在样本数据中，有 60 位女生的每周平均体育运动时间超过 4 小时，请完成每周平均 体育运动时间与性别列联表，并判断是否有 95%的把握认为“该校学生的每周平均体育运 动时间与性别有关”． P(K2≥k0) 0.10 0.05 0.010 0.005 k0 2.706 3.841 6.635 7.879 附：K2＝ n（ad－bc）2 （a＋b）（c＋d）（a＋c）（b＋d） 17．解： (1)300× 4500 15 000 ＝90，所以应收集 90 位女生的样本数据． (2)由频率分布直方图得每周平均体育运动超过 4 小时的频率为 1－2×(0.100＋0.025)＝ 0.75，所以该校学生每周平均体育运动时间超过 4 小时的概率的估计值为 0.75. (3)由(2)知，300 位学生中有 300×0.75＝225(位)的每周平均体育运动时间超过 4 小时， 75 人的每周平均体育运动时间不超过 4 小时．又因为样本数据中有 210 份是关于男生的， 90 份是关于女生的，所以每周平均体育运动时间与性别列联表如下： 男生 女生 总计 每周平均体育运动时间不超过 4 小时 45 30 75 每周平均体育运动时间超过 4 小时 165 60 225 总计 210 90 300 结合列联表可算得 K2＝300×（165×30－45×60）2 75×225×210×90 ＝100 21 ≈4.762>3.841. 所以有 95%的把握认为“该校学生的每周平均体育运动时间与性别有关”． 18．I2[2014·北京卷] 从某校随机抽取 100 名学生，获得了他们一周课外阅读时间(单位： 小时)的数据，整理得到数据分组及频数分布表和频率分布直方图(如图 16)． 组号 分组 频数 1 [0，2) 6 2 [2，4) 8 3 [4，6) 17 4 [6，8) 22 5 [8，10) 25 6 [10，12) 12 7 [12，14) 6 8 [14，16) 2 9 [16，18) 2 合计 100 图 16 (1)从该校随机选取一名学生，试估计这名学生该周课外阅读时间少于 12 小时的概率； (2)求频率分布直方图中的 a，b 的值； (3)假设同一组中的每个数据可用该组区间的中点值代替，试估计样本中的 100 名学生 该周课外阅读时间的平均数在第几组．(只需写出结论) 18．解：(1)根据频数分布表，100 名学生中课外阅读时间不少于 12 小时的学生共有 6 ＋2＋2＝10(名)，所以样本中的学生课外阅读时间少于 12 小时的频率是 1－ 10 100 ＝0.9. 故从该校随机选取一名学生，估计其课外阅读时间少于 12 小时的概率为 0.9. (2)课外阅读时间落在组[4，6)内的有 17 人，频率为 0.17，所以 a＝频率 组距 ＝0.17 2 ＝0.085. 课外阅读时间落在组[8，10)内的有 25 人，频率为 0.25，所以 b＝频率 组距 ＝0.25 2 ＝0.125. (3)样本中的 100 名学生课外阅读时间的平均数在第 4 组． 20．I2，K2[2014·福建卷] 根据世行 2013 年新标准，人均 GDP 低于 1035 美元为低收 入国家；人均 GDP 为 1035～4085 美元为中等偏下收入国家；人均 GDP 为 4085～12 616 美 元为中等偏上收入国家；人均 GDP 不低于 12 616 美元为高收入国家．某城市有 5 个行政区， 各区人口占该城市人口比例及人均 GDP 如下表： 行政区 区人口占城市人口比例 区人均 GDP(单位：美元) A 25% 8000 B 30% 4000 C 15% 6000 D 10% 3000 E 20% 10 000 (1)判断该城市人均 GDP 是否达到中等偏上收入国家标准； (2)现从该城市 5 个行政区中随机抽取 2 个，求抽到的 2 个行政区人均 GDP 都达到中等 偏上收入国家标准的概率． 20．解：(1)设该城市人口总数为 a，则该城市人均 GDP 为 8000×0.25a＋4000×0.30a＋6000×0.15a＋3000×0.10a＋10 000×0.20a a ＝ 6400(美元)． 因为 6400∈[4085，12 616)， 所以该城市人均 GDP 达到了中等偏上收入国家标准． (2)“从 5 个行政区中随机抽取 2 个”的所有的基本事件是： {A，B}，{A，C}，{A，D}，{A，E}，{B，C}，{B，D}，{B，E}，{C，D}，{C，E}， {D，E}，共 10 个． 设事件 M 为“抽到的 2 个行政区人均 GDP 都达到中等偏上收入国家标准”， 则事件 M 包含的基本事件是：{A，C}，{A，E}，{C，E}，共 3 个． 所以所求概率为 P(M)＝ 3 10. 6．I2[2014·广东卷] 为了解 1000 名学生的学习情况，采用系统抽样的方法，从中抽取 容量为 40 的样本，则分段的间隔为( ) A．50 B．40 C．25 D．20 6．C [解析] 由题意得，分段间隔是1000 40 ＝25. 17．I2、K2[2014·湖南卷] 某企业有甲、乙两个研发小组，为了比较他们的研发水平， 现随机抽取这两个小组往年研发新产品的结果如下： (a，b)，(a，b)，(a，b)，(a，b)，(a，b)，(a，b)，(a，b)，(a，b)，(a，b)，(a，b)，(a， b)，(a，b)，(a，b)，(a，b)，(a，b)． 其中 a，a 分别表示甲组研发成功和失败；b，b 分别表示乙组研发成功和失败． (1)若某组成功研发一种新产品，则给该组记 1 分，否则记 0 分．试计算甲、乙两组研 发新产品的成绩的平均数和方差，并比较甲、乙两组的研发水平． (2)若该企业安排甲、乙两组各自研发一种新产品，试估计恰有一组研发成功的概率． 17．解：(1)甲组研发新产品的成绩为 1，1，1，0，0，1，1，1，0，1，0，1，1，0，1， 其平均数为 x 甲＝10 15 ＝2 3 ， 方差为 s2甲＝ 1 15 1－2 3 2 ×10＋ 0－2 3 2 ×5 ＝2 9. 乙组研发新产品的成绩为 1，0，1，1，0，1，1，0，1，0，0，1，0，1，1， 其平均数为 x 乙＝ 9 15 ＝3 5 ， 方差为 s2乙＝ 1 15 1－3 5 2 ×9＋ 0－3 5 2 ×6 ＝ 6 25. 因为 x 甲＞x 乙，s2甲＜s2乙，所以甲组的研发水平优于乙组． (2)记 E＝{恰有一组研发成功}． 在所抽得的 15 个结果中，恰有一组研发成功的结果是(a，b)，(a，b)，(a，b)，(a，b)， (a，b)，(a，b)，(a，b)， 共 7 个，故事件 E 发生的频率为 7 15. 将频率视为概率，即得所求概率为 P(E)＝ 7 15. 6．I2[2014·江苏卷] 为了了解一片经济林的生长情况，随机抽测了其中 60 株树木的底 部周长(单位：cm)，所得数据均在区间[80，130]上，其频率分布直方图如图 12 所示，则在 抽测的 60 株树木中，有____株树木的底部周长小于 100 cm. 图 12 6．24 [解析] 由频率分布直方图可得，数据在[80，90]的频率为 0.015×10＝0.15，数 据在[90，100]的频率为 0.025×10＝0.25.又样本容量为 60 株，故所求为(0.15＋0.25)×60＝ 24(株)． 19．I2[2014·新课标全国卷Ⅱ] 某市为了考核甲、乙两部门的工作情况，随机访问了 50 位市民．根据这 50 位市民对这两部门的评分(评分越高表明市民的评价越高)，绘制茎叶图 如下： 甲部门 乙部门 3 5 9 4 4 0 4 4 8 9 7 5 1 2 2 4 5 6 6 7 7 7 8 9 9 7 6 6 5 3 3 2 1 1 0 6 0 1 1 2 3 4 6 8 8 9 8 8 7 7 7 6 6 5 5 5 5 5 4 4 4 3 3 3 2 1 0 0 7 0 0 1 1 3 4 4 9 6 6 5 5 2 0 0 8 1 2 3 3 4 5 6 3 2 2 2 0 9 0 1 1 4 5 6 10 0 0 0 图 14 (1)分别估计该市的市民对甲、乙两部门评分的中位数； (2)分别估计该市的市民对甲、乙两部门的评分高于 90 的概率； (3)根据茎叶图分析该市的市民对甲、乙两部门的评价． 19．解：(1)由所给茎叶图知，将 50 位市民对甲部门的评分由小到大排序，排在第 25， 26 位的是 75，75，故样本的中位数为 75，所以该市的市民对甲部门评分的中位数的估计值 是 75. 50 位市民对乙部门的评分由小到大排序，排在第 25，26 位的是 66，68，故样本中位数 为66＋68 2 ＝67，所以该市的市民对乙部门评分的中位数的估计值是 67. (2)由所给茎叶图知，50 位市民对甲、乙部门的评分高于 90 的比率分别为 5 50 ＝0.1，8 50 ＝ 0.16，故该市的市民对甲、乙部门的评分高于 90 的概率的估计值分别为 0.1，0.16. (3)由所给茎叶图知，市民对甲部门的评分的中位数高于对乙部门的评分的中位数，而 且由茎叶图可以大致看出对甲部门的评分的标准差要小于对乙部门的评分的标准差，说明该 市市民对甲部门的评价较高、评价较为一致，对乙部门的评价较低、评价差异较大．(注： 考生利用其他统计量进行分析，结论合理的同样给分．) 18．I2[2014·全国新课标卷Ⅰ] 从某企业生产的某种产品中抽取 100 件，测量这些产品 的一项质量指标值，由测量结果得如下频数分布表： 质量指标 值分组 [75，85) [85，95) [95，105) [105，115) [115，125) 频数 6 26 38 22 8 (1)在答题卡上作出这些数据的频率分布直方图； (2)估计这种产品质量指标值的平均值及方差(同一组中的数据用该组区间的中点值作代 表); (3)根据以上抽样调查数据，能否认为该企业生产的这种产品符合“质量指标值不低于 95 的产品至少要占全部产品 80%”的规定？ 18．解：(1)频率分布直方图如下： (2)质量指标值的样本平均数为 x＝80×0.06＋90×0.26＋100×0.38＋110×0.22＋120×0.08＝100. 质量指标值的样本方差为 s2＝(－20)2×0.06＋ (－10)2×0.26＋0×0.38＋102×0.22＋202×0.08＝104.所以这种产品质量指标值的平均 数的估计值为 100，方差的估计值为 104. (3)质量指标值不低于 95 的产品所占比例的估计值为 0.38＋0.22＋0.8＝0.68. 由于该估计值小于 0.8，故不能认为该企业生产的这种产品符合“质量指标值不低于 95 的产品至少要占全部产品 80%”的规定． 8．I2[2014·山东卷] 为了研究某药品的疗效，选取若干名志愿者进行临床试验，所有志 愿者的舒张压数据(单位：kPa)的分组区间为[12，13)，[13，14)，[14，15)，[15，16)，[16， 17]．将其按从左到右的顺序分别编号为第一组，第二组，……，第五组，图 12 是根据试 验数据制成的频率分布直方图，已知第一组与第二组共有 20 人，第三组中没有疗效的有 6 人，则第三组中有疗效的人数为( ) 图 12 A．6 B．8 C．12 D．18 8．C [解析] 因为第一组与第二组共有 20 人，并且根据图像知第一组与第二组的频率 之比是 0.24∶0.16＝3∶2，所以第一组的人数为 20×3 5 ＝12.又因为第一组与第三组的频率之 比是 0.24∶0.36＝2∶3 ，所以第三组有 12÷2 3 ＝18 人．因为第三组中没有疗效的人数为 6， 所以第三组中有疗效的人数是 18－6＝12. 16．I2，K2[2014·山东卷] 海关对同时从 A，B，C 三个不同地区进口的某种商品进行抽 样检测，从各地区进口此种商品的数量(单位：件)如表所示．工作人员用分层抽样的方法从 这些商品中共抽取 6 件样品进行检测． 地区 A B C 数量 50 150 100 (1)求这 6 件样品中来自 A，B，C 各地区商品的数量； (2)若在这 6 件样品中随机抽取 2 件送往甲机构进行进一步检测，求这 2 件商品来自相 同地区的概率． 16．解：(1)因为样本容量与总体中的个体数的比是 6 50＋150＋100 ＝ 1 50 ，所以样本中包含三个地区的个体数量分别是：50× 1 50 ＝1，150× 1 50 ＝3，100× 1 50 ＝2. 所以 A，B，C 三个地区的商品被选取的件数分别是 1，3，2. (2)设 6 件来自 A，B，C 三个地区的样品分别为：A；B1，B2，B3；C1，C2.则抽取的这 2 件商品构成的所有基本事件为： {A，B1}，{A，B2}，{A，B3}，{A，C1}，{A，C2}，{B1，B2}，{B1，B3}，{B1，C1}， {B1，C2}，{B2，B3}{B2，C1}，{B2，C2}，{B3，C1}，{B3，C2}，{C1，C2}，共 15 个． 每个样品被抽到的机会均等，因此这些基本事件的出现是等可能的． 记事件 D 为“抽取的这 2 件商品来自相同地区”， 则事件 D 包含的基本事件有{B1，B2}，{B1，B3}，{B2，B3}，{C1，C2}，共 4 个． 所以 P(D)＝ 4 15 ，即这 2 件商品来自相同地区的概率为 4 15. 9．I2[2014·陕西卷] 某公司 10 位员工的月工资(单位：元)为 x1，x2，…，x10，其均值和 方差分别为 x－和 s2，若从下月起每位员工的月工资增加 100 元，则这 10 位员工下月工资的 均值和方差分别为( ) A. x－，s2＋1002 B. x－＋100，s2＋1002 C. x－，s2 D. x－＋100，s2 9．D [解析] 由题目中所给的数据可知 xx1＋x2＋x3＋…＋x10 10 ， 不妨设这 10 位员工下月工资的均值为 y－，则 y－＝（x1＋x2＋x3＋…＋x10）＋1000 10 ＝ x－＋ 100，易知方差没发生变化． 2．I1、I2[2014·四川卷] 在“世界读书日”前夕，为了了解某地 5000 名居民某天的阅 读时间，从中抽取了 200 名居民的阅读时间进行统计分析．在这个问题中，5000 名居民的 阅读时间的全体是( ) A．总体 B．个体 C．样本的容量 D．从总体中抽取的一个样本 2．A [解析] 根据抽样统计的概念可知，统计分析的对象全体叫做“总体”．故选 A. 17．I2、K2[2014·重庆卷] 20 名学生某次数学考试成绩(单位：分)的频率分布直方图如 图 13 所示． 图 13 (1)求频率分布直方图中 a 的值； (2)分别求出成绩落在[50，60)与[60，70)中的学生人数； (3)从成绩在[50，70)的学生中任选 2 人，求此 2 人的成绩都在[60，70)中的概率． 17．解：(1)据直方图知组距为 10，由 (2a＋3a＋7a＋6a＋2a)×10＝1， 解得 a＝ 1 200 ＝0.005. (2)成绩落在[50，60)中的学生人数为 2×0.005×10×20＝2. 成绩落在[60，70)中的学生人数为 3×0.005×10×20＝3. (3)记成绩落在[50，60)中的 2 人为 A1，A2，成绩落在[60，70)中的 3 人为 B1，B2，B3， 则从成绩在[50，70)的学生中任选 2 人的基本事件共有 10 个，即(A1，A2)，(A1，B1)，(A1， B2)，(A1，B3)，(A2，B1)，(A2，B2)，(A2，B3)，(B1，B2)，(B1，B3)，(B2，B3)． 其中 2 人的成绩都在[60，70)中的基本事件有 3 个，即(B1，B2)，(B1，B3)，(B2，B3)． 故所求概率为 P＝ 3 10. I3 正态分布 I4 变量的相关性与统计案例 17．I2、I4[2014·安徽卷] 某高校共有学生 15 000 人，其中男生 10 500 人，女生 4500 人．为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集 300 位学生 每周平均体育运动时间的样本数据(单位：小时)． (1)应收集多少位女生的样本数据？ (2)根据这 300 个样本数据，得到学生每周平均体育运动时间的频率分布直方图(如图 14 所示)，其中样本数据的分组区间为：[0，2]，(2，4]，(4，6]，(6，8]，(8，10]，(10，12]．估 计该校学生每周平均体育运动时间超过 4 小时的概率． 图 14 (3)在样本数据中，有 60 位女生的每周平均体育运动时间超过 4 小时，请完成每周平均 体育运动时间与性别列联表，并判断是否有 95%的把握认为“该校学生的每周平均体育运 动时间与性别有关”． P(K2≥k0) 0.10 0.05 0.010 0.005 k0 2.706 3.841 6.635 7.879 附：K2＝ n（ad－bc）2 （a＋b）（c＋d）（a＋c）（b＋d） 17．解： (1)300× 4500 15 000 ＝90，所以应收集 90 位女生的样本数据． (2)由频率分布直方图得每周平均体育运动超过 4 小时的频率为 1－2×(0.100＋0.025)＝ 0.75，所以该校学生每周平均体育运动时间超过 4 小时的概率的估计值为 0.75. (3)由(2)知，300 位学生中有 300×0.75＝225(位)的每周平均体育运动时间超过 4 小时， 75 人的每周平均体育运动时间不超过 4 小时．又因为样本数据中有 210 份是关于男生的， 90 份是关于女生的，所以每周平均体育运动时间与性别列联表如下： 男生 女生 总计 每周平均体育运动时间不超过 4 小时 45 30 75 每周平均体育运动时间超过 4 小时 165 60 225 总计 210 90 300 结合列联表可算得 K2＝300×（165×30－45×60）2 75×225×210×90 ＝100 21 ≈4.762>3.841. 所以有 95%的把握认为“该校学生的每周平均体育运动时间与性别有关”． 6．I4[2014·湖北卷] 根据如下样本数据 x 3 4 5 6 7 8 y 4.0 2.5 －0.5 0.5 －2.0 －3.0 得到的回归方程为y^＝bx＋a，则( ) A．a＞0，b＜0 B．a＞0，b＞0 C．a＜0，b＜0 D．a＜0，b＞0 6．A [解析] 作出散点图如下： 由图像不难得出，回归直线y^＝bx＋a 的斜率 b<0，截距 a>0，所以 a>0，b<0.故选 A. 图 11 7．I4[2014·江西卷] 某人研究中学生的性别与成绩、视力、智商、阅读量这 4 个变量的 关系，随机抽查了 52 名中学生，得到统计数据如表 1 至表 4，则与性别有关联的可能性最 大的变量是( ) 表 1 表 2 成绩 性别 不及格 及格 总计 男 6 14 20 女 10 22 32 总计 16 36 52 视力 性别 好 差 总计 男 4 16 20 女 12 20 32 总计 16 36 52 表 3 表 4 智商 性别 偏高 正常 总计 男 8 12 20 女 8 24 32 总计 16 36 52 阅读量 性别 丰富 不丰 富 总计 男 14 6 20 女 2 30 32 总计 16 36 52 A．成绩 B．视力 C．智商 D．阅读量 7．D [解析] 通过计算可得，表 1 中的χ2≈0.009，表 2 中的χ2≈1.769，表 3 中的χ2＝ 1.300，表 4 中的χ2≈23.481，故选 D. 18．I4、K2[2014·辽宁卷] 某大学餐饮中心为了解新生的饮食习惯，在全校一年级学生 中进行了抽样调查，调查结果如下表所示： 喜欢甜品 不喜欢甜品 合计 南方学生 60 20 80 北方学生 10 10 20 合计 70 30 100 (1)根据表中数据，问是否有 95%的把握认为“南方学生和北方学生在选用甜品的饮食 习惯方面有差异”； (2)已知在被调查的北方学生中有 5 名数学系的学生，其中 2 名喜欢甜品，现在从这 5 名学生中随机抽取 3 人，求至多有 1 人喜欢甜品的概率． 附：χ2＝n（n11n22－n12n21）2 n1＋n2＋n＋1n＋2 ， P(χ2≥k) 0.100 0.050 0.010 k 2.706 3.841 6.635 18．解：(1)将 2×2 列联表中的数据代入公式计算，得 χ2＝n（n11n22－n12n21）2 n1＋n2＋n＋1n＋2 ＝100×（60×10－20×10）2 70×30×80×20 ＝100 21 ≈4.762. 由于 4.762＞3.841，所以有 95%的把握认为“南方学生和北方学生在选用甜品的饮食习 惯方面有差异”． (2)从 5 名数学系学生中任取 3 人的一切可能结果所组成的基本事件空间Ω＝{(a1，a2， b1)，(a1，a2，b2)，(a1，a2，b3)，(a1，b1，b2)，(a1，b1，b3)，(a1，b2，b3)，(a2，b1，b2)，(a2， b1，b3)，(a2，b2，b3)，(b1，b2，b3)}， 其中 ai 表示喜欢甜品的学生，i＝1，2，bj 表示不喜欢甜品的学生，j＝1，2，3. Ω由 10 个基本事件组成，且这些基本事件的出现是等可能的． 用 A 表示“3 人中至多有 1 人喜欢甜品”这一事件，则 A＝{(a1，b1，b2)，(a1，b1，b3)， (a1，b2，b3)，(a2，b1，b2)，(a2，b1，b3)，(a2，b2，b3)，(b1，b2，b3)}． 事件 A 由 7 个基本事件组成，因而 P(A)＝ 7 10. I5 单元综合 17．I5[2014·广东卷] 某车间 20 名工人年龄数据如下表： 年龄(岁) 工人数(人) 19 1 28 3 29 3 30 5 31 4 32 3 40 1 合计 20 (1)求这 20 名工人年龄的众数与极差； (2)以十位数为茎，个位数为叶，作出这 20 名工人年龄的茎叶图； (3)求这 20 名工人年龄的方差． 1．[2014·株洲模拟] 通过随机询问 110 名大学生是否爱好某项运动，得到如下列联表： 男 女 总计 爱好 40 20 60 不爱好 20 30 50 总计 60 50 110 由 K2＝ n（ad－bc）2 （a＋b）（c＋d）（a＋c）（b＋d） ，得 K2＝110×（40×30－20×20）2 60×50×60×50 ≈7.8. 附表： P(K2≥k) 0.050 0.010 0.001 k 3.841 6.635 10.828 参照附表，得到的正确结论是( ) A．有 99%以上的把握认为“爱好该项运动与性别有关” B．有 99%以上的把握认为“爱好该项运动与性别无关” C．在犯错误的概率不超过 0.1%的前提下，认为“爱好该项运动与性别有关” D．在犯错误的概率不超过 0.1%的前提下，认为“爱好该项运动与性别无关” 1．A [解析] 因为 7.8>6.635，所以选项 A 正确． 2．[2014·济南期末] 为了调查城市 PM2.5 的情况，按地域把 48 个城市分成大型、中型、 小型三组，相应的城市数分别为 8，16，24.若用分层抽样的方法抽取 12 个城市，则应抽取 的中型城市数为( ) A．3 B．4 C．5 D．6 图 X331 2．B [解析] 根据分层抽样的特点可知，抽样比例为12 48 ＝1 4 ，则应抽取的中型城市数为 16×1 4 ＝4. 3．[2014·长沙四校联考] 为了了解某同学的数学学习情况，对他的 6 次数学测试成绩(满 分 100 分)进行统计，作出的茎叶图如图 X331 所示，则下列关于该同学数学成绩的说法正 确的是( ) A．中位数为 83 B．众数为 85 C．平均数为 85 D．方差为 19 3．C [解析] 易知该同学的 6 次数学测试成绩的中位数为 84，众数为 83，平均数为 85. 8．[2014·湖南长郡中学月考] 为了研究高中学生对乡村音乐的态度(喜欢和不喜欢两种 态度)与性别的关系，运用 2×2 列联表进行独立性检验，经计算 K2＝8.01，则认为“喜欢乡 村音乐与性别有关系”的把握性约为( ) P(K2≥k0) 0.100 0.050 0.025 0.010 0.001 k0 2.706 3.841 5.024 6.635 10.828 A.0.1% B．1% C．99% D．99.9% 8．C [解析] 因为 K2＝8.01>6.635，所以有 99%以上的把握认为“喜欢乡村音乐与性 别有关系”． 9．[2014·衡阳模拟] 已知某总体由编号为 01，02，…，19，20 的 20 个个体组成．利用 下面的随机数表选取 5 个个体，选取方法是从随机数表中第 1 行的第 5 列和第 6 列的数字开 始由左到右依次选取两个数字，则选出来的第 5 个个体的编号为( ) 7816 6572 0802 6314 0702 4369 9728 0198 3204 9234 4935 8200 3623 4869 6938 7481 A.08 B．07 C．02 D．01 9．D [解析] 从随机数表第 1 行的第 5 列和第 6 列的数字开始由左到右依次选取两个 数字，依次为 65，72，08，02，63，14，07，02，43，69，97，28，01，98，…，其中 08， 02，14，07，01 符合条件，故选 D. 10．[2014·湖南师大附中月考] 某厂对一批元件的长度(单位：mm)进行抽样检测，得到 如图 X332 所示的频率分布直方图．若长度在区间[90，96)内的元件为合格品，则估计这批 产品的合格率是( ) A．70% B．75% C．80% D．85% 图 X332 10．C [解析] 易知在区间[90，96)内的直方图的面积 S＝1－(0.027 5＋0.027 5＋0.045 0)×2＝0.8，故合格率是 80%.