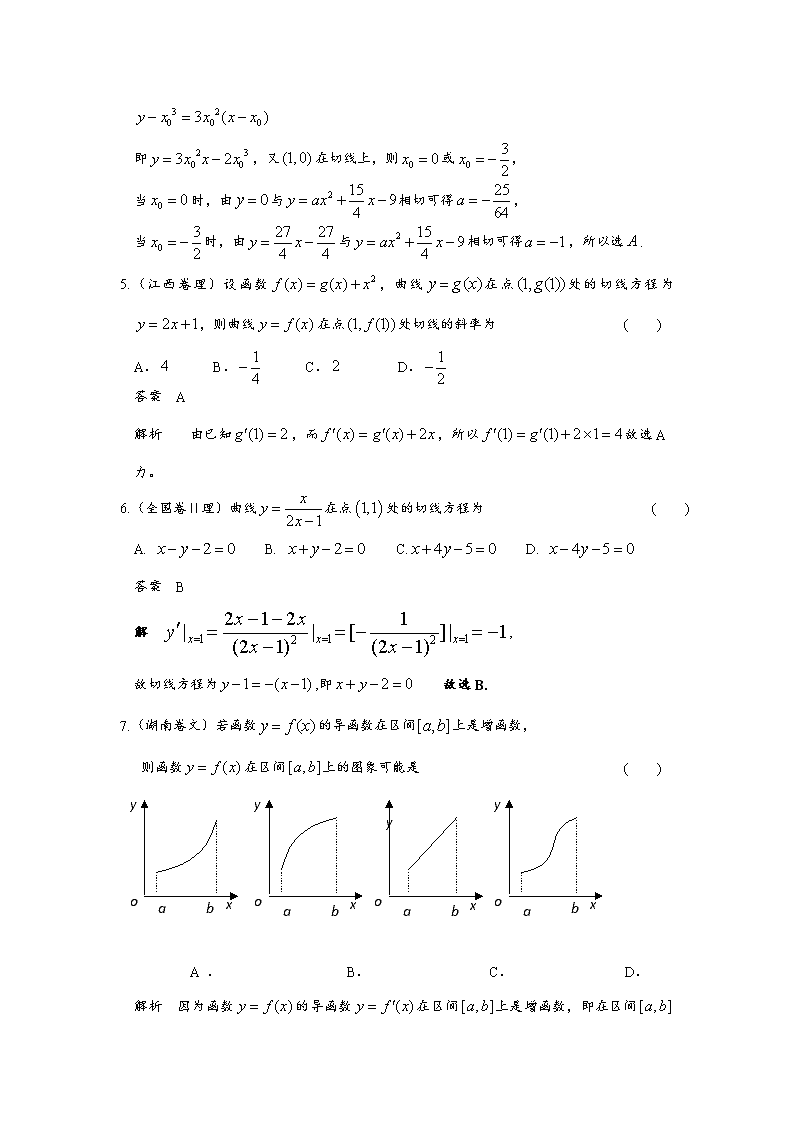- 182.50 KB
- 2021-04-21 发布
近年导数高考选择题汇总
1.(广东卷文)函数的单调递增区间是 ( )
A. B.(0,3) C.(1,4) D.
答案 D
解析 ,令,解得,故选D
2.(全国卷Ⅰ理) 已知直线y=x+1与曲线相切,则α的值为( )
A.1 B. 2 C.-1 D.-2
答案 B
解:设切点,则,又
.故答案 选B
3.(安徽卷理)已知函数在R上满足,则曲线
在点处的切线方程是 ( )
A. B. C. D.
答案 A
解析 由得几何,
即,∴∴,∴切线方程,即选A
4.(江西卷文)若存在过点的直线与曲线和都相切,则等于 ( )
A.或 B.或 C.或 D.或
答案 A
解析 设过的直线与相切于点,所以切线方程为
即,又在切线上,则或,
当时,由与相切可得,
当时,由与相切可得,所以选.
5.(江西卷理)设函数,曲线在点处的切线方程为,则曲线在点处切线的斜率为 ( )
A. B. C. D.
答案 A
解析 由已知,而,所以故选A
力。
6.(全国卷Ⅱ理)曲线在点处的切线方程为 ( )
A. B. C. D.
答案 B
解 ,
故切线方程为,即 故选B.
7.(湖南卷文)若函数的导函数在区间上是增函数,
则函数在区间上的图象可能是 ( )
y
a
b
a
b
a
o
x
o
x
y
b
a
o
x
y
o
x
y
b
A . B. C. D.
解析 因为函数的导函数在区间上是增函数,即在区间
上各点处的斜率是递增的,由图易知选A. 注意C中为常数噢.
8.(辽宁卷理)若满足2x+=5, 满足2x+2(x-1)=5, += ( )
A. B.3 C. D.4
答案 C
解析 由题意 ①
②
所以,
即2
令2x1=7-2t,代入上式得7-2t=2log2(2t-2)=2+2log2(t-1)
∴5-2t=2log2(t-1)与②式比较得t=x2
于是2x1=7-2x2
9.(天津卷理)设函数则 ( )
A在区间内均有零点。
B在区间内均无零点。
C在区间内有零点,在区间内无零点。
D在区间内无零点,在区间内有零点。
【考点定位】本小考查导数的应用,基础题。
解析 由题得,令得;令得;得,故知函数在区间上为减函数,在区间
为增函数,在点处有极小值;又
,故选择D。
相关文档
- 2020版高考历史大一轮复习 必考部2021-04-21 20:19:147页
- 2014高考英语一轮复习自选训练 阅2021-04-21 20:19:025页
- 高考真题——语文辽宁卷2021-04-21 20:17:0412页
- 高考化学第一轮复习课件第1讲 重2021-04-21 20:16:517页
- 高考数学专题复习:《抛物线》同步训2021-04-21 20:16:0710页
- 大连民族学院附中创新设计高考数学2021-04-21 20:13:545页
- 2020届二轮复习近五年高考英语短文2021-04-21 20:13:3521页
- 2020高考物理刷题增分:计算题仿真202021-04-21 20:13:293页
- 2020版高考地理一轮复习 第12章 世2021-04-21 20:13:196页
- 2016届高考数学(理)5年高考真题备考2021-04-21 20:12:468页