- 855.00 KB
- 2021-04-21 发布
数学试题 文
第I卷(选择题)
一、单选题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个符合题目要求)
1.以一个等边三角形的底边所在的直线为旋转轴旋转一周所得的几何体是
A.一个圆柱 B.一个圆锥 C.两个圆锥 D.一个圆台
2.如图,为四边形的斜二测直观图,则原平面图形是( )
A.直角梯形 B.等腰梯形
C.非直角且非等腰的梯形 D.不可能是梯形
3.已知直线是平面的斜线,则内不存在与( )
A.相交的直线 B.平行的直线 C.异面的直线 D.垂直的直线
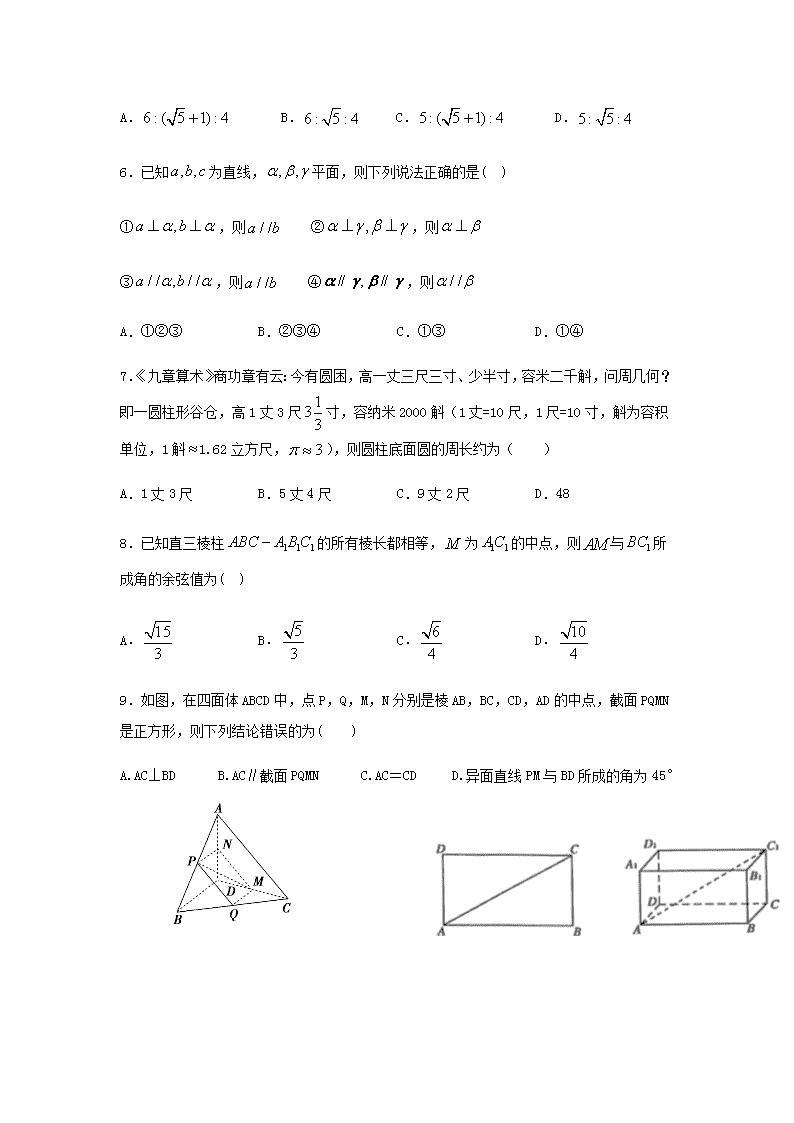
4.一个几何体的三视图如图所示,则这个几何体的体积为( )
A. B. C. D.
第4题 第5题
5.如图,一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径相等,这时圆柱、圆锥、球的表面积之比为( )
A. B. C. D.
6.已知为直线,平面,则下列说法正确的是( )
①,则 ②,则
③,则 ④,则
A.①②③ B.②③④ C.①③ D.①④
7.《九章算术》商功章有云:今有圆困,高一丈三尺三寸、少半寸,容米二千斛,问周几何?即一圆柱形谷仓,高1丈3尺寸,容纳米2000斛(1丈=10尺,1尺=10寸,斛为容积单位,1斛1.62立方尺,),则圆柱底面圆的周长约为( )
A.1丈3尺 B.5丈4尺 C.9丈2尺 D.48
8.已知直三棱柱的所有棱长都相等,为的中点,则与所成角的余弦值为( )
A. B. C. D.
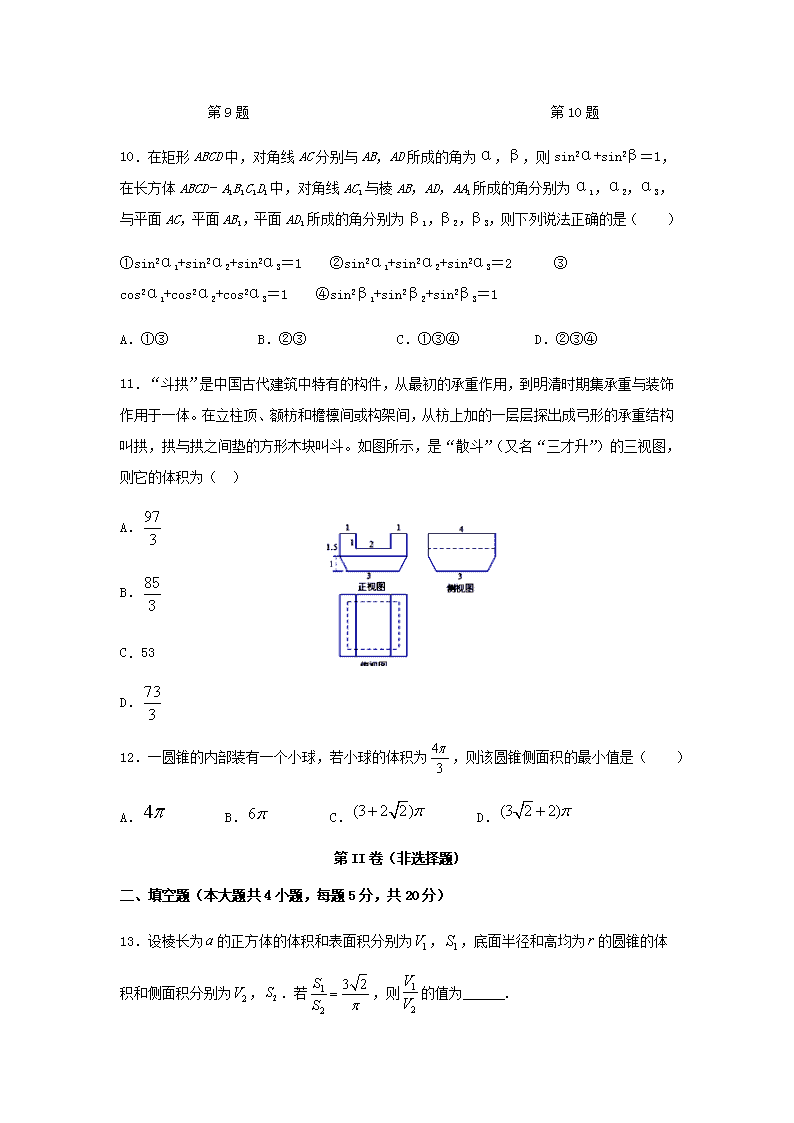
9.如图,在四面体ABCD中,点P,Q,M,N分别是棱AB,BC,CD,AD的中点,截面PQMN是正方形,则下列结论错误的为( )
A.AC⊥BD B.AC∥截面PQMN C.AC=CD D.异面直线PM与BD所成的角为45°
第9题 第10题
10.在矩形ABCD中,对角线AC分别与AB,AD所成的角为α,β,则sin2α+sin2β=1,在长方体ABCD﹣A1B1C1D1中,对角线AC1与棱AB,AD,AA1所成的角分别为α1,α2,α3,与平面AC,平面AB1,平面AD1所成的角分别为β1,β2,β3,则下列说法正确的是( )
①sin2α1+sin2α2+sin2α3=1 ②sin2α1+sin2α2+sin2α3=2 ③cos2α1+cos2α2+cos2α3=1 ④sin2β1+sin2β2+sin2β3=1
A.①③ B.②③ C.①③④ D.②③④
11.“斗拱”是中国古代建筑中特有的构件,从最初的承重作用,到明清时期集承重与装饰作用于一体。在立柱顶、额枋和檐檩间或构架间,从枋上加的一层层探出成弓形的承重结构叫拱,拱与拱之间垫的方形木块叫斗。如图所示,是“散斗”(又名“三才升”)的三视图,则它的体积为( )
A.
B.
C.53
D.
12.一圆锥的内部装有一个小球,若小球的体积为,则该圆锥侧面积的最小值是( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,每题5分,共20分)
13.设棱长为的正方体的体积和表面积分别为,,底面半径和高均为的圆锥的体积和侧面积分别为,.若,则的值为______.
14.球的内接圆柱的表面积为,侧面积为,则该球的表面积为_______
15.如图是表示一个正方体表面的一种平面展开图,图中的四条线段
、、和在原正方体中相互异面的有__________对.
16.如图所示,在直角梯形中,分别是
的中点,将三角形沿折起,下列说法正确的是__________(填上所有正确的序号).
①不论折至何位置(不在平面内)都有平面;
②不论折至何位置都有;
③不论折至何位置(不在平面内)都有.
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题10分)从斜二测画法下的棱长为a的空心正方体的直观图中分离出来的.
(Ⅰ)求直观图中的面积;
(Ⅱ) 如果用图示中这样一个装置来盛水,
那么最多能盛多少体积的水?
18.(本小题12分)如图所示,在正方体中,为的中点,为的中点.
求证:(1)四点共面;
(2)三线共点.
第18题 第19题
19.(本小题12分)如图1所示,在等腰梯形,,,垂足为,,.将沿折起到的位置,使平面平面,如图2所示,点为棱的中点.
(1)求证:平面;
(2)求证:平面;
(3)求三棱锥的体积.
20.(本小题12分)如图,四棱柱的底面是平行四边形,且,,,为的中点,平面.
(1)证明:平面平面;
(2)若,试求异面直线与所成角的余弦值.
21.(本小题12分)如图,四棱锥中,平面,,,,为中点.
(Ⅰ)证明:CE//平面;
(Ⅱ)求直线与平面所成角的正弦值.
22.(本小题12分)如图,已知点P在圆柱OO1的底面⊙O上,分别为⊙O、⊙O1的直径,且平面.
(1)求证:;
(2)若圆柱的体积,在线段AP上是否存在一点M,使异面直线OM与所成角的余弦值为?若存在,请指出M的位置,并证明;若不存在,请说明理由.
数学答案(文)
一、选择题
1、C 2.A 3.B 4.A 5.A 6.D
7.B 8.D 9.C 10.D 11.B 12.C
二、填空题
13. 14. 15.3 16.①②
三、解答题
17.(Ⅰ)……….5分
(Ⅱ)………….5分
18. 证明:(1)连接.
∵分别是和的中点,
∴.
又,
∴四边形是平行四边形,
∴,∴,
∴与确定一个平面,
∴四点共面.………….6分
(2)由(1)知,,且,
∴直线与必相交,设.
∵平面,,
∴平面.
又平面,,
∴平面,即是平面与平面的公共点,
又平面平面,
∴,
∴三线共点.……….12分
19.
20.(1)见解析;(2)
(1),
是正三角形,,
,即,
平面,平面,,
,平面,
平面,平面平面.….5分
(2)取的中点,连接、,连接,
△中,是中位线,
,,
四边形是平行四边形,可得
,
(或其补角)是异面直线与所成的角.
,
,,,
,即异面直线与所成角的余弦值为………..12分
21、(Ⅰ)证明:取中点,连接,,
则由中位线可知,,
∴四边形是平行四边形,∴,
又平面,平面,
∴平面………5分
(Ⅱ)∵平面,故.
在直角梯形中,,,,
∴.∵,∴. ∴平面.
过点作,垂足为,则,
∴平面,
则即为直线与平面所成的角,如图,
易求:,,
又点为的中点,.
由面积法得:.所以.
在中,.
……….12分
22.(1)见解析;(2)①,②见解析
(1)证明:∵P在⊙O上,AB是⊙O的直径,
平面 又,
平面,又平面,故.
……..5分
(2)在AP上存在一点M,当M为AP的中点时,使异面直线OM与所成角的余弦值为.
证明:∵O、M分别为的中点,则,
就是异面直线OM与所成的角,
又,
在中,.
∴在AP上存在一点M,当M为AP的中点时,使异面直线OM与所成角的余弦值为.
…….12分