数学卷·2017届河北省定州中学高三（高补班）上学期周练（11 9页

河北定州中学2016-2017学年第一学期 高四数学周练试题（10）‎ 一、单项选择题 ‎1．设有一个回归方程为，则变量增加一个单位时（ ）‎ A．平均减少2.5个单位 B．平均增加2.5个单位 ‎ C．平均增加2个单位 D．平均减少2个单位 ‎2．函数的定义域为（ ）‎ ‎（A） （B）‎ ‎（C） （D）‎ ‎3．已知复数满足，则（ ）‎ A． B． C． D．‎ ‎4．已知数列{an}满足a1=1，，则254是该数列的（ ）‎ A．第14项 B．第12项 C．第10项 D．第8项 ‎5．自然数按照下表的规律排列，则上起第2013行，左起第2014列的数为( )‎ A. B. ‎ C. D. 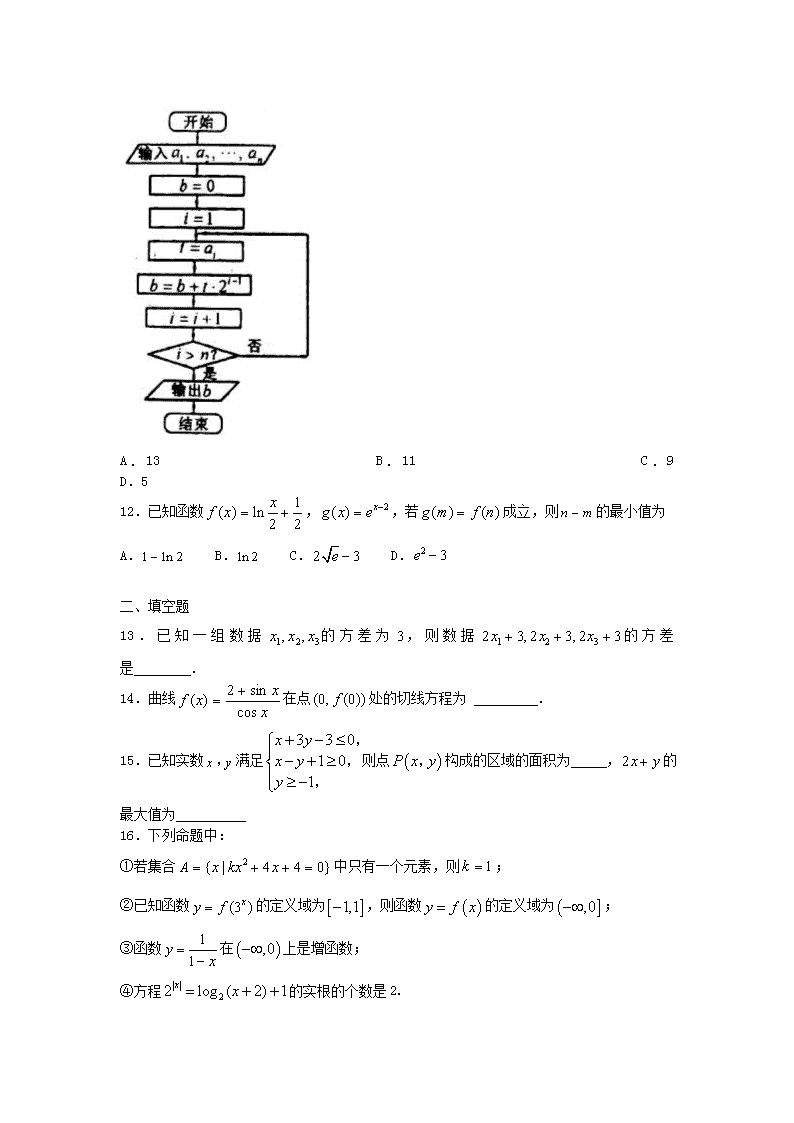‎ ‎6．设全集，函数的定义域为，集合，则的元素个数为（ ）‎ A．1 B‎.2 C．3 D．4‎ ‎7．已知复数，且有，则（ ）‎ A．5 B． C．3 D．‎ ‎8．设实数列和分别是等差数列与等比数列，且，，则以下结论正确的是（ ）‎ A． B． C． D．‎ ‎9．集合则（ ）‎ A． B． C． D．‎ ‎10．一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个等腰直角三角形，则该几何体外接球的体积为（ ）‎ A． B． C． D．3‎ ‎11．如下图所示的程序框图，若输入，则输出的（ ）‎ A．13 B．‎11 C．9 D．5‎ ‎12．已知函数，，若成立，则的最小值为 A． B． C． D．‎ 二、填空题 ‎13．已知一组数据的方差为，则数据的方差是 ．‎ ‎14．曲线在点处的切线方程为 ．‎ ‎15．已知实数满足则点构成的区域的面积为 ，的最大值为 ‎ ‎16．下列命题中：‎ ‎①若集合中只有一个元素，则；‎ ‎②已知函数的定义域为，则函数的定义域为；‎ ‎③函数在上是增函数；‎ ‎④方程的实根的个数是2.‎ 所有正确命题的序号是 （请将所有正确命题的序号都填上）‎ 三、解答题 ‎17．如图，直三棱柱ABC﹣A1B‎1C1中，D，E分别是AB，BB1的中点．‎ ‎（1）证明BC1∥平面A1CD ‎（2）设AA1=AC=CB=2，AB=2，求三棱锥C﹣A1DE的体积．‎ ‎18．设平面三点.‎ ‎（1）试求向量的模；‎ ‎（2）试求向量与夹角的余弦值；‎ ‎（3）试求与垂直的单位向量的坐标.‎ ‎19．设函数.‎ ‎ （1）讨论的单调性和极值；‎ ‎ （2）证明：当时，若存在零点，则在区间上仅有一个零点.‎ ‎20．某位同学为了研究气温对饮料销售的影响，经过对某小卖部的统计，得到一个卖出的某种饮料杯数与当天气温的对比表．他分别记录了‎3月21日至‎3月25日的白天平均气温（）与该小卖部的这种饮料销量（杯），得到如下数据：‎ 日期 ‎3月21日 ‎3月22日 ‎3月23日 ‎3月24日 ‎3月25日 平均气温 ‎8‎ ‎10‎ ‎14‎ ‎11‎ ‎12‎ 销量（杯）‎ ‎21‎ ‎25‎ ‎35‎ ‎26‎ ‎28‎ ‎（1）若先从这五组数据中任取2组，求取出的2组数据恰好是相邻2天数据的概率；‎ ‎（2）请根据所给五组数据，求出关于的线回归方程；‎ ‎（3）根据（2）中所得的线性回归方程，若天气预报‎3月26日的白天平均气温7（‎ ‎），请预测该小卖部这种饮料的销量．（参考公式：）‎ ‎21．已知椭圆的右焦点为F2（1，0），点在椭圆上．‎ ‎（1）求椭圆方程；‎ ‎（2）点在圆上，M在第一象限，过M作圆的切线交椭圆于P、Q 两点，问|F2P|+|F2Q|+|PQ|是否为定值？如果是，求出定值，如不是，说明理由．‎ ‎22．关于的方程有两个相等的实数根．‎ ‎（1）求实数的取值范围；‎ ‎（2）若，求的值．‎ 参考答案 ACAAC CBBCA ‎ ‎11．A ‎12．B ‎13．‎ ‎14．‎ ‎15．8，11‎ ‎16． ③④.‎ ‎17．（Ⅰ）连接AC1 交A‎1C于点F，则DF为三角形ABC1的中位线，故DF∥BC1．再根据直线和平面平行的判定定理证得BC1∥平面A1CD．（Ⅱ）由题意可得此直三棱柱的底面ABC为等腰直角三角形，由D为AB的中点可得CD⊥平面ABB‎1A1．求得CD的值，利用勾股定理求得A1D、DE和A1E的值，可得A1D⊥DE．进而求得S△A1DE的值，再根据三棱锥C-A1DE的体积为•S△A1DE•CD，运算求得结果 试题解析：（1）证明：连结AC1交A‎1C于点F，则F为AC1中点又D是AB中点，‎ 连结DF，则BC1∥DF． 3分 因为DF⊂平面A1CD，BC1不包含于平面A1CD， 4分 所以BC1∥平面A1CD． 5分 ‎（2）解：因为ABC﹣A1B‎1C1是直三棱柱，所以AA1⊥CD．由已知AC=CB，D为AB的中点，所以CD⊥AB．又AA1∩AB=A，于是CD⊥平面ABB‎1A1． 8分 由AA1=AC=CB=2，得∠ACB=90°，，，，A1E=3，故A1D2+DE2=A1E2，即DE⊥A1D 10分 所以三菱锥C﹣A1DE的体积为：==1． 12分 ‎18．（1）；（2）；（3）或 解：（1）依题意，，∴，∴.‎ ‎（2）∵，，，所以.‎ ‎（3）设与垂直的单位向量，，则 ‎，解得或，∴所求单位向量或.‎ ‎19．（1）①当时，在上单调递增，无极值，②当时的单调递减区间是，单调递增区间是，在处取得极小值；（2）证明见解析.‎ ‎（1）的定义域为，‎ ‎，‎ ‎①当时，，在上单调递增，无极值，‎ ‎②当，由，解得，‎ 与在区间上的情况如下：‎ 所以，的单调递减区间是，单调递增区间是；‎ 所以在处取得极小值.‎ ‎（2）由（1）知，在区间上的最小值为.‎ 因为存在零点，所以，从而.‎ 当时，在区间上单调递减，且，‎ 所以是在区间上的唯一零点.‎ 当时，在区间上单调递减，且，，‎ 所以在区间上仅有一个零点.‎ 综上可知，当时，若存在零点，则在区间上仅有一个零点.‎ ‎20．（1）；（2）；（3）.‎ ‎（1）设“选取的2组数据恰好是相邻2天数据”为事件，‎ 所以．‎ ‎（2）由数据，求得 由公式，求得，‎ ‎∴关于的线性回归方程为．‎ ‎（3）当时，，‎ 所以该小卖部这种饮料的销量大约为18杯．‎ ‎21．解：（1）右焦点为，‎ 左焦点为，点在椭圆上 ‎，‎ 所以椭圆方程为 ‎（2）设 ，‎ 连接OM，OP，由相切条件知 同理可求 所以为定值．‎ ‎22．解：（1）关于的方程有两个相等的实数根，‎ 所以，则．‎ 因为，所以．即所求实数的取值范围为．‎ ‎（2）‎ 当时，则，‎ 平方得，∴，‎ 即．‎