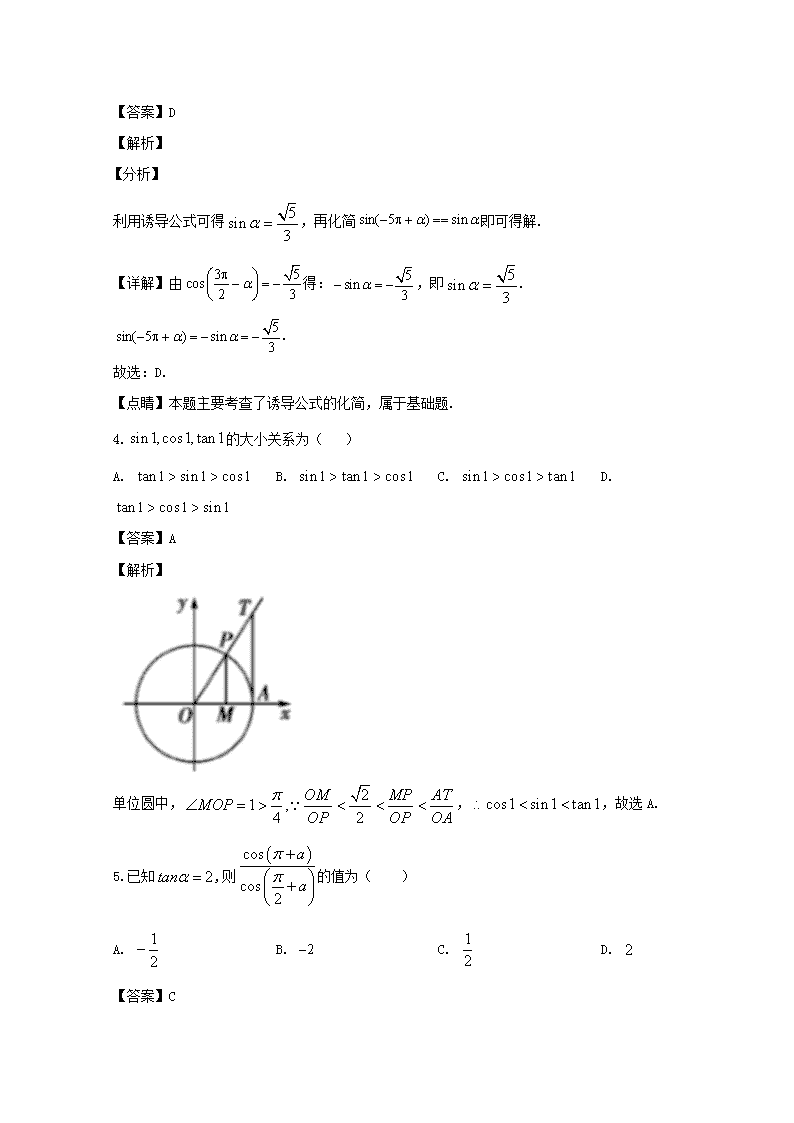- 1.06 MB
- 2021-04-21 发布
www.ks5u.com
数学试卷
一、选择题(每小题5分,共60分)
1.的值为 ( )
A. B. C. D.
【答案】B
【解析】
【分析】
利用诱导公式可得所求之值.
【详解】,故选B.
【点睛】本题考查诱导公式,属于基础题.
2.设集合,则=
A. B. C. D.
【答案】C
【解析】
试题分析:由补集的概念,得,故选C.
【考点】集合的补集运算
【名师点睛】研究集合的关系,处理集合的交、并、补的运算问题,常用韦恩图、数轴等几何工具辅助解题.一般地,对离散的数集、抽象的集合间的关系及运算,可借助韦恩图,而对连续的集合间的运算及关系,可借助数轴的直观性,进行合理转化.
3.若,则( )
A. B. C. D.
【答案】D
【解析】
分析】
利用诱导公式可得,再化简即可得解.
【详解】由得:,即.
.
故选:D.
【点睛】本题主要考查了诱导公式的化简,属于基础题.
4.的大小关系为( )
A. B. C. D.
【答案】A
【解析】
单位圆中,,,故选A.
5.已知,则的值为( )
A. B. C. D.
【答案】C
【解析】
【分析】
直接利用诱导公式化简结合弦化切可得解.
【详解】,
故选:C.
【点睛】本题主要考查了诱导公式及同角三角函数基本关系,属于基础题.
6.等于( )
A. 4 B. -4 C. D.
【答案】B
【解析】
【分析】
直接利用结合对数运算即可得解.
【详解】.
故选:B.
【点睛】本题主要考查了对数的运算,即可得解.
7.下列函数在区间(0,2)上必有零点的是( )
A. B. C. D.
【答案】D
【解析】
【分析】
通过求函数的零点,验证是否在(0,2)即可得解.
【详解】对于A,令,得,
对于B,,所以不存在零点;
对于C,令,解得;
对于D,令,得.
故选:D.
【点睛】本题主要考查了函数零点的概念,属于基础题.
8.使不等式-2sinx≥0成立的x的取值集合是( )
A.
B.
C.
D.
【答案】C
【解析】
【分析】
首先对三角不等式进行恒等变换,变换成sinx,进一步利用单位圆求解.
【详解】2sinx≥0
解得:sinx
进一步利用单位圆解得:(k∈Z)
故选C.
【点睛】本题考查的知识要点:利用单位元解三角不等式,特殊角的三角函数值.
9.的一条对称轴方程为( )
A. B. C. D.
【答案】A
【解析】
【分析】
令,即可得解.
【详解】令,解得:.
当时,轴为:.
故选:A.
【点睛】本题主要考查了正弦型函数的对称轴的求解,属于基础题.
10.函数是( )
A. 周期为的偶函数 B. 周期为的奇函数
C. 周期为的奇函数 D. 周期为的偶函数
【答案】A
【解析】
【分析】
化简函数,进而可得周期和奇偶性.
【详解】函数.
周期.
且,为偶函数.
故选:A.
【点睛】本题主要考查了诱导公式化简三角函数,及判断三角函数的奇偶性,属于基础题.
11.函数x的最小值、最大值分别是( )
A. B. C. D.
【答案】A
【解析】
由于,故函数的最小值为 ,最大值为 .
故选A.
12.函数的最小值是( )
A. B. C. D. 不存在
【答案】C
【解析】
【分析】
令,则,再根据二次函数性质求最值即可.
【详解】令,则.
当时,有最小值.
故选:C.
【点睛】本题主要考查了三角函数与二次函数复合函数求最值,考查了换元法,属于基础题.
二、填空题(每小题5分,共20分)
13.函数的单调递减区间是_______________.
【答案】
【解析】
【分析】
由,令,即可得解.
【详解】,
令,
解得.
故答案为:.
【点睛】本题主要考查了正切型函数的单调区间的求解,考查了整体代换的思想,属于基础题.
14.已知扇形的周长是6,中心角是1弧度,则该扇形的面积为________.
【答案】2
【解析】
试题分析:设扇形的弧长为,半径为.则有,解得.则扇形的面积为.
考点:扇形的面积.
15.已知角终边上一点,则______________.
【答案】
【解析】
【分析】
由任意角三角函数定义得,讨论和即可得解.
【详解】由任意角三角函数定义得:.
当时,;
当时,;
故答案为:.
【点睛】本题主要考查了任意角三角函数的定义,涉及分类讨论的思想,属于基础题.
16.已知,则的值是_______________.
【答案】2
【解析】
【分析】
由代入原式中替换1,再分子分母同时除以,结合正切值即可得解.
【详解】由.
因为,所以原式.
故答案为:2.
【点睛】本题主要考查了同角三角函数关系的妙用,属于基础题.
三、解答题(17题10分,18-22每题12分)
17.已知函数的定义域是,值域是,求a,b的值.
【答案】或
【解析】
分析】
先求得,再讨论和两种情况求值域列方程求解即可.
【详解】当时,,.
当时,值域为:,
所以,解得,
当时,值域为:,
所以,解得,
综上:或.
【点睛】本题主要考查了余弦型三角函数的值域问题,考查了分类讨论的思想及整体代换的思想,属于中档题.
18.已知求下列各式的值:
(1)
(2)
【答案】(1);(2).
【解析】
【分析】
(1)利用,将平方再根据角的范围开方即可得解;
(2)将平方再根据角的范围开方即可得解
【详解】(1)由,
当时,,
所以.
(2)由,
当时,,
所以.
【点睛】本题主要考查了的应用,属于基础题.
19.已知.
(1)化简.
(2)若是第三象限角,且,求的值.
(3)若,求的值.
【答案】(1);(2);(3).
【解析】
【分析】
(1)直接利用诱导公式化简即可得解;
(2)利用诱导公式化简得,结合角的范围和同角三角函数关系可得解;
(3)直接代入,结合诱导公式化简求值即可.
详解】(1).
(2) ,所以.
因为是第三象限角,所以.
所以.
(3) 时, .
【点睛】本题主要考查了诱导公式的化简及同角三角函数的关系的求解,属于基础题.
20.已知.
(1)求的定义域;
(2)讨论的单调性;
(3).求在区间上的值域.
【答案】(1);(2)在上增函数;(3)
【解析】
【分析】
(1)直接令真数大于0即可得解;
(2)由和,结合同增异减即可得解;
(3)直接利用(2)的单调性可直接得值域.
【详解】(1)由,得,解得.
所以定义域为:;
(2)由在上为增函数,且为增函数,
所以在上为增函数;
(3)由(2)知函数单调递增, ,.
所以在区间上的值域为.
【点睛】本题主要考查了对数与指数函数的复合函数,考查了复合函数的“同增异减”的应用,属于基础题.
21.已知函数是奇函数,且.
(1)求;
(2)求函数f(x)的单调增区间.
【答案】(1);(2)(开闭都对)
【解析】
【分析】
(1)由,结合可得解;
(2)令,可得解.
【详解】(1)函数是奇函数,所以,
解得:.
又,所以;
(2).
令,解得:.
所以增区间为:.(开闭都对)
【点睛】本题主要考查了三角函数的奇偶性和单调性,属于基础题.
22.已知
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性,并说明理由;
(3)在上作出函数f(x)的图像.
【答案】(1);(2)奇函数;(3)见解析.
【解析】
【分析】
(1)由分母不等于0即可得定义域;
(2)利用奇函数定义判断,从而得解;
(3)直接去绝对值得分段函数,可得图像.
【详解】(1)由可得:,所以.
所以定义域为:;
(2)由(1)知函数的定义域关于原点对称,
,所以为奇函数;
(3) .
【点睛】本题主要考查了三角函数奇偶性的判断及正切函数的作图,涉及分段函数的表示,属于基础题.
23.已知函数
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间上的值域.
【答案】(1);(2).
【解析】
【分析】
(1)利用二倍角公式化简函数为,进而利用周期公式可得解;
(2)先求,从而可得,进而可得值域.
详解】(1)
.
所以最小正周期为:.
(2) 由,可得:.
所以.
所以f(x) 在区间上的值域为:.
【点睛】本题主要考查了三角函数的二倍角公式化简及整体代换求值域,属于基础题.