- 93.00 KB
- 2021-04-21 发布
平行线等分线段定理
一.练习
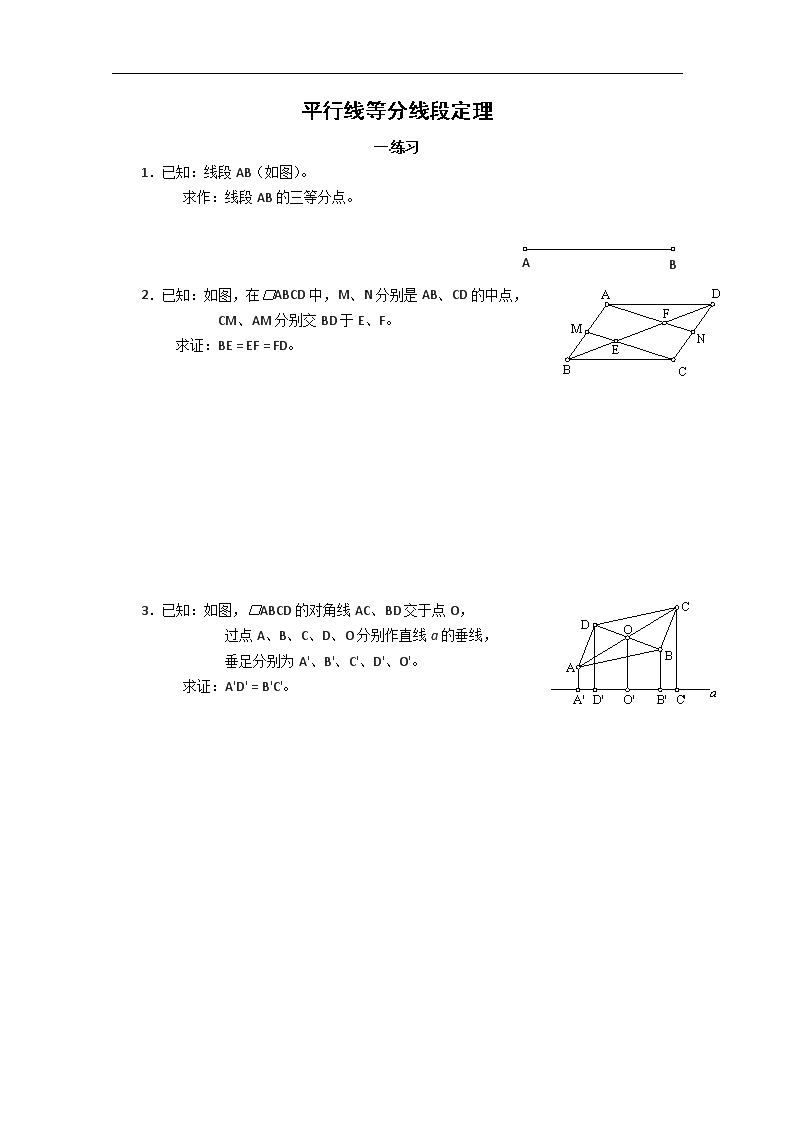
1.已知:线段 AB(如图)。
求作:线段 AB 的三等分点。
2.已知:如图,在□ABCD 中,M、N 分别是 AB、CD 的中点,
CM、AM 分别交 BD 于 E、F。
求证:BE = EF = FD。
3.已知:如图,□ABCD 的对角线 AC、BD 交于点 O,
过点 A、B、C、D、O 分别作直线 a 的垂线,
垂足分别为 A'、B'、C'、D'、O'。
求证:A'D' = B'C'。
A B
Ł
ł C
D
nm
f
e
。
a
B
c
d o
❁❄ ❏ ❂❃
二、达标检测
1.已知:如图,在梯形 ABCD 中,AB//CD,E 是 CD 的中点,
EF//BC 交 AB 于 F,FG// BD 交 AD 于 G。
求证:AG = DG。
2.如图,在△ABC 中,D 是 AB 的中点,DE//BC 交 AC 于 E,EF//AB 交 BC 于 F。
(1)求证:BF=CF;
(2)图中与 DE 相等的线段有 ; (3)图中与 EF 相等的线段有 ;
(4)连结 DF,则 DF 与 AC 的位置关系是 ,数量关系是 。
三.提升
1.求证:直角梯形的两个直角顶点到对腰中点的距离相等。
2.已知:如图,AD 是△ABC 的中线,E 是 AD 的中点,AE 的延长线交 AC 于 F。
求证:FC = 2AF。
a
b c
dg
f e
Ɂ
B C
D
F
a
b cd
e
f