- 1.63 MB
- 2021-04-21 发布
2016-2017 学年度第二学期期中考试
高二理科数学试题
一、选择题(本大题共 40 小题,每小题 3 分,共 120 分.在每小题给出的四个选项中,
只有一项是符合题目要求的)
1.已知全集 ,则集合
( )
A. B. C. D.
2.下列四组函数中表示同一函数的是( )
A. , B.
C. , D. ,
3.函数 的值域是( )
A.(-∞,4) B.(0,+∞) C.(0,4] D.[4,+∞)
4.若函数 是定义在 上的奇函数,且在区间 上是减函数,则不等式
的解集为( )
A. B. C. D.
5. 函数 且 过定点( )
A. B. C. D.
6.已知 ,则 a,b,c 的大小关系为( )
A.b<a<c B.c<a<b C.c<b<a D.b<c<a
7. 函数 的递减区间是( )
A. B. C. D.
8.函数 的大致图象为( )
9.函数 的零点所在的区间是( )
A. B.(1,2) C.(2,e) D.(e,3)
10.对于命题:①平行于同一直线的两个平面平行;②平行于
同一平面的两个平面平行;③垂直于同一直线的两直线平行;④垂直于同一平面的两直线平
行.其中正确的个数有( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
11.如图,正四面体 的棱长均为 ,且 平面 于 A,点 B,C,D 均
在平面 外,且在平面 同一侧,则点 B 到平面 的距离是( )
A. B. C. D.
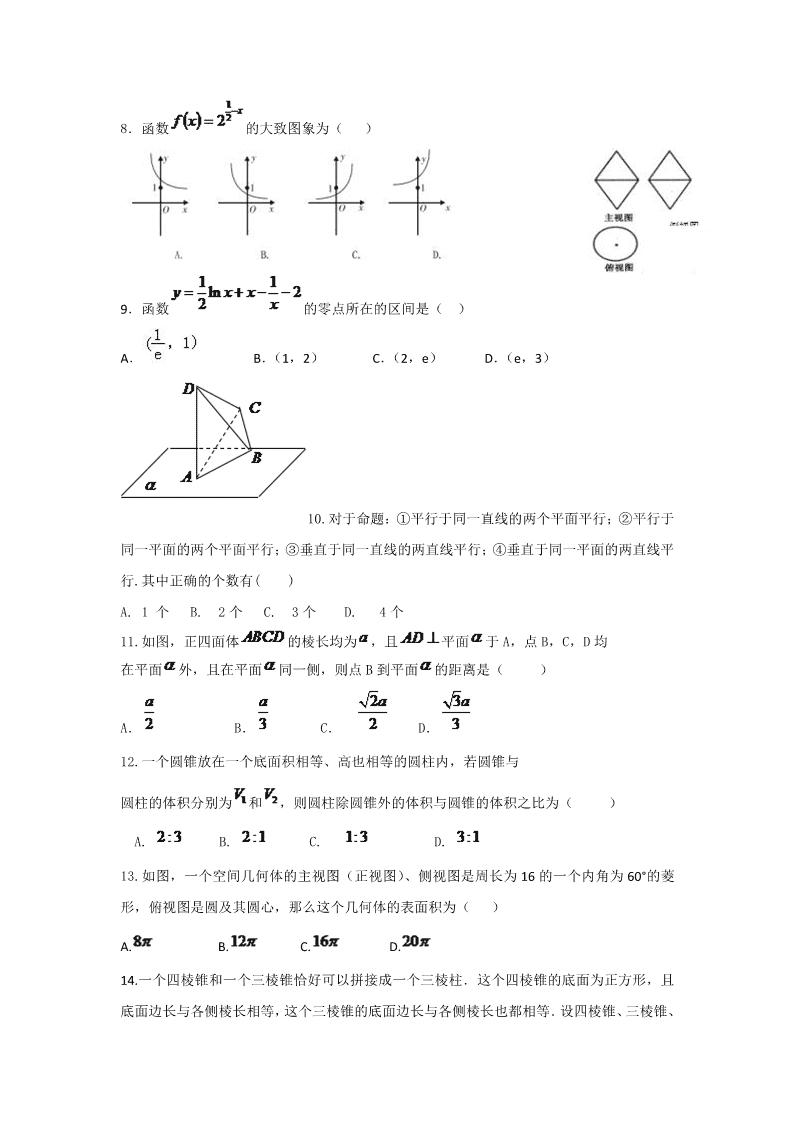
12.一个圆锥放在一个底面积相等、高也相等的圆柱内,若圆锥与
圆柱的体积分别为 和 ,则圆柱除圆锥外的体积与圆锥的体积之比为( )
A. B. C. D.
[]
13.如图,一个空间几何体的主视图(正视图)、侧视图是周长为 16 的一个内角为 60°的菱
形,俯视图是圆及其圆心,那么这个几何体的表面积为( )
A. B. C. D.
14.一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱.这个四棱锥的底面为正方形,且
底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等.设四棱锥、三棱锥、
三棱柱的高分别为 , , ,则 等于( )
A. B. C. D.
15.斜率为 2 的直线经过点(3,5),(a,7),(-1,b)三点,则 a、b 的值为( )
A.a=4,b=0 B.a=-4,b=-3 C.a=4,b=-3 D.a=-4,b=3
16.若直线(a+2)x+(1-a)y=3 与直线(a-1)x+(2a+3)y+2=0 互相垂直,则 a 等于( )[来 A.1
B.-1 C.±1 D.-2
17.已知 A(2,4)与 B(3,3)关于直线 l 对称,则直线 l 的方程为( )
A.x+y=0 B.x-y=0 C.x+y-6=0 D.x-y+1=0
18.若直线 l 与直线 y=1,x=7,分别交于点 P,Q,且线段 PQ 的中点坐标为(1,-1),则
直线 l 的斜率为( )
A.
1
3 B.-
1
3 C.-
3
2 D.
2
3
19.已知点 A(-3,-4),B(6,3)到直线 l:ax+y+1=0 的距离相等,则实数 a 的值为( )
A.
7
9 B.-
1
3 C.-
7
9或-
1
3 D.
7
9 或
1
3
20.圆:x2+y2-4x+6y=0 和圆:x2+y2-6x=0 交于 A,B 两点,则 AB 的垂直平分线的方程是( )
A. B. C. D.
21.已知圆 经过 A(5,2),B(-1,4)两点,圆心在 轴上,则圆 的方程是( )
A.(x-2)2+y2=13 B.(x+2)2+y2=17 C.(x+1)2+y2=40 D.(x-1)2+y2=20
22.已知 A(1-t, 1-t, t),B(2,t,t),则 A,B 两点间距离的最小值为 ( )
A. B. C. D.
23. 当 a 为任意实数时,直线(a-1)x-y+a+1=0 恒过定点 C,则以 C 为圆心,半径为
的圆的方程为 ( )
A.x2+y2-2x+4y=0 B.x2+y2+2x+4y=0 C.x2+y2+2x-4y=0 D.x2+y2-2x-4y=0
24. 直线 截圆(x-2)2+y2=4 所得劣弧所对的圆心角是 ( )
A. B. C. D.
25.直线 与圆 在第一象限内有两个不同的交点,则 m 取值范围是
A. B. C. D.
26. 曲线 y=1+ [-2,2])与直线 y=k(x-2)+4 有两个公共点时,实数 k 的取值范
围是( )
A. B. C. D.
27. 如果执行下面的程序框图,那么输出的 ( )
A.2450 B.2500 C.2550 D.2652
28.下列各进制中,最大的值是( )
A. B. C. D.
29.1337 与 382 的最大公约数是( )
A.191 B.382 C.201 D.37
30.已知 ,应用秦九韶算法计算 时的值时, 的值为( )
A.27 B.11 C.109 D.36
31.下列说法中,正确的是( ).
A.数据 5,4,4,3,5,2 的众数是 4
B.一组数据的标准差是这组数据的方差的平方
C.数据 2,3,4,5 的标准差是数据 4,6,8,10 的标准差的一半
D.频率分布直方图中各小长方形的面积等于相应各组的频数
32.从集合{1,2,3,4,5}中,选出由 3 个数组成子集,使得这 3 个数中任何两个数的和
不等于 6,则取出这样的子集的概率为( ).
A. B. C. D.
33. 如图,在圆心角为直角的扇形 OAB 中,分别以 OA,OB 为直径作两个半圆, 在扇形
OAB 内随机取一点,则此点取自阴影部分的概率是( )
A.
1
2-
1
π B.
1
π C.1-
2
π D.
2
π
34.函数 , 的部分图象如图所示,则 的
值分别是( )
A.2, B.2, C.4, D.4,
35.已知函数 , ,则下列结论中正确的是
( )
A.函数 y= f(x)·g(x)的最小正周期为
B.函数 y= f(x)·g(x)的最大值为 1
C.将函数 y= f(x)的图象向右平移 单位后得 g(x)的图象
D.将函数 y= f(x)的图象向左平移 单位后得 g(x)的图象
36. 下列命题中正确的个数是( )
①若 e 为单位向量,且 a∥e,则 a=|a|e;
②若 a 与 b 共线,又 b 与 c 共线,则 a 与 c 必共线;
③a·a·a=|a|3;
④若平面内有四点 A,B,C,D,则必有
AC
→+
BD
→=
BC
→+
AD
→.
A.1 B.2 C.3 D.4
37.在△ABC 中,a,b,c 分别是角 A,B,C 的对边,若 a2+b2=2c2,则 cos C 的最小值
为( )
A.
3
2 B.
2
2 C. -
1
2 D.
1
2
38.若关于 x,y 的不等式组
x+y≤2,
y≥ax 表示的平面区域为一个三角形及其内部,则实数 a 的
取值范围是( )
A.(-∞,1) B.(0,1) C.(1,+∞) D.(-1,1)
39.若{an}是等比数列,其公比是 q,且-a5,a4,a6 成等差数列,则 q 等于( )
A.1 或 2 B.-1 或 2 C.1 或-2 D.-1 或-2
40.已知等差数列{an}的前 n 项和为 Sn,若
OA
→=a2
OB
→+a2 017
OC
→,且 A,B,C 三点共线(该直
线不过原点 O),则 S2 018 的值为( )
A.1 007 B.2 018 C.1 009 D.2 007
二、解答题(本大题共 3 小题,共 30 分.解答应写出文字说明,证明过程或演算步骤)
41.已知函数 f(x)=lo (a2-3a+3)x.
(1)判断函数的奇偶性;
(2)若 y=f(x)在(-∞,+∞)上为减函数,求 a 的取值范围.
42. 的内角 A,B,C 的对边分别为 a,b,c,已知
(I)求 C;
(II)若 的面积为 ,求 的周长.
43. 已知数列 的前 n 项和 Sn=3n2+8n, 是等差数列,且
(I)求数列 的通项公式;
(II)令 求数列 的前 n 项和 Tn.
高二理科数学试题答案:
1—5 CCCBD 6—10 CAACB 11—15 ABCBC 16—20 CDBCC
21—25 DBCDD 26—30 DCBAD 31—35 CDCAC 36—40 ADDBC
41.解:(1)函数 f(x)=lo (a2-3a+3)x 的定义域为 R.
又 f(-x)=lo (a2-3a+3)-x= - lo (a2-3a+3)x= - f(x),
(2)若 f(x)=lo (a2-3a+3)x 在(-∞,+∞)上为减函数,则 y=(a2-3a+3)x 在(-∞,+∞)上为增函数,
由指数函数的单调性,有 a2-3a+3>1,[解得 a<1 或 a>2.
所以 a 的取值范围是(-∞,1)∪(2,+∞).
42.【答案】(I) ;(II) .
试题解析:(I)由已知及正弦定理得 ,
由已知及余弦定理得, .
故 ,从而 .
所以 的周长为 .
43.【答案】(I) ;(II) .
试题解析:(I)由题意知当 时, ,
当 时, ,所以 .
设数列 的公差为 ,
由 ,即 ,可解得 ,
所以 .
(II)由(I)知 ,
又 ,
得 ,
,
两式作差,得
所以