2017-2018学年黑龙江省齐齐哈尔市第八中学高二3月月考数学（理）试题 Word版 7页

2017-2018 学年黑龙江省齐齐哈尔市第八中学高二 3 月月考数学(理)试题 命题人:高保华 审题人:李庆瑞 第一部分 选择题（共 60 分） 一、选择题:本大题共 12 小题，每小题 5 分，共 60 分，在每小题给出的四个选项中，只有一 项是符合题目要求的 1.设集合 }034{ 2  xxxA ， }032{  xxB ，则 A B I （ ） A． )2 3,3(  B． )2 3,3( C． )2 3,1( D． )3,2 3( 2. 4 2 1 dxx 等于 （ ） A． 2ln 2 B． 2ln 2 C． ln2 D． ln 2 3．下列函数中， 0x  是其极值点的函数是 ( ) A．   3f x x  B．   cosf x x  C．   sinf x x x  D．   1f x x  4、函数   2 ln 2f x x x  的单调递减区间是 ( ) A． 20, 2      B． 2 ,2     C． 2, 2      ， 20, 2      D． 2 ,02      ， 20, 2      5．下列四个命题中真命题的个数是 （ ） (1)“ 1x  ”是“ 2 3 2 0x x   ”的充分不必要条件； (2)命题“ Rx  ， sin 1x  ”的否定是“ Rx  ，sin 1x  ”； (3)“若 2 2am bm ，则 a b ”的逆命题为真命题； (4)命题 :p  1,x   ， lg 0x  ，命题 :q Rx  ， 2 1 0x x   ，则 p q 为真命题； A． 0 B．1 C． 2 D．3 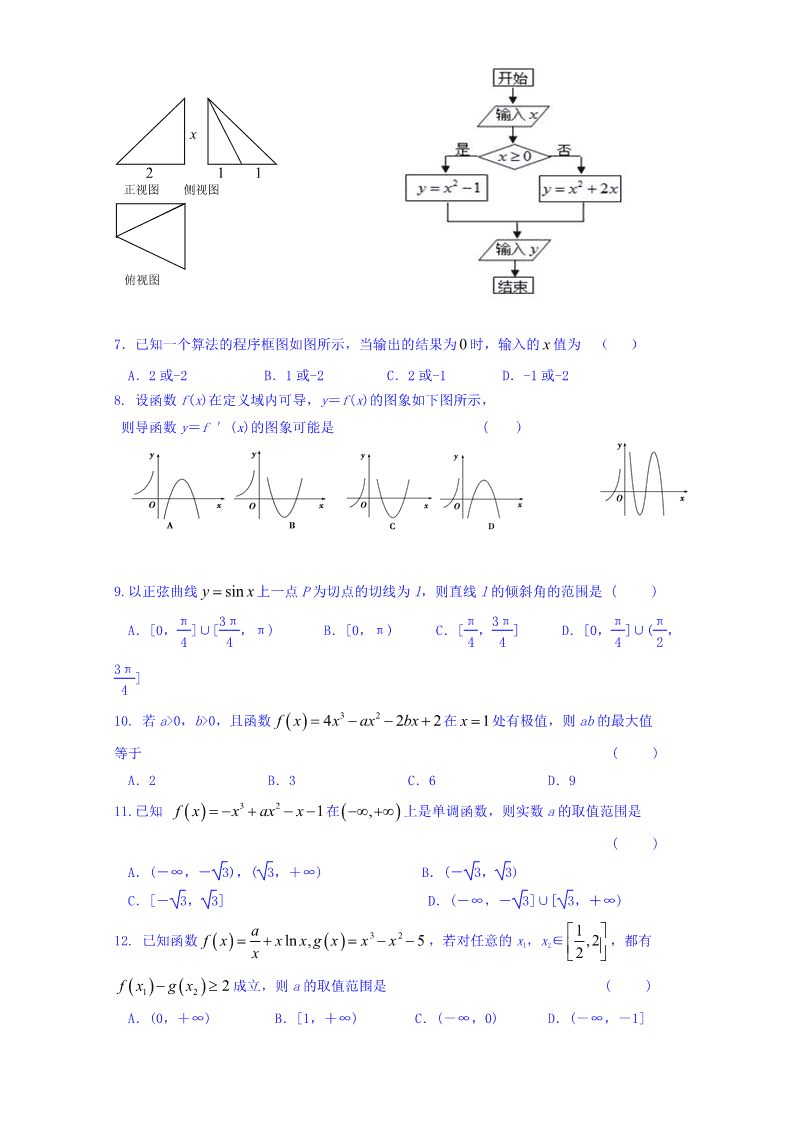6．某几何体的三视图如图所示，且该几何体的体积是 3，则正视图中的 x 的值是（ ） A． 2 B． 9 2 C． 3 D． 3 2 2 1 1 正视图 侧视图 俯视图 x 7．已知一个算法的程序框图如图所示，当输出的结果为 0 时，输入的 x 值为 （ ） A．2 或-2 B．1 或-2 C．2 或-1 D．-1 或-2 8. 设函数 f(x)在定义域内可导，y＝f(x)的图象如下图所示， 则导函数 y＝f ′(x)的图象可能是 ( ) 9.以正弦曲线 siny x 上一点 P 为切点的切线为 l，则直线 l 的倾斜角的范围是 ( ) A．[0，π 4 ]∪[3π 4 ，π) B．[0，π) C．[π 4 ，3π 4 ] D．[0，π 4 ]∪(π 2 ， 3π 4 ] 10. 若 a>0，b>0，且函数   3 24 2 2f x x ax bx    在 1x  处有极值，则 ab 的最大值 等于 ( ) A．2 B．3 C．6 D．9 11.已知   3 2 1f x x ax x     在 ,  上是单调函数，则实数 a 的取值范围是 ( ) A．(－∞，－ 3)，( 3，＋∞) B．(－ 3， 3) C．[－ 3， 3] D．(－∞，－ 3]∪[ 3，＋∞) 12. 已知函数     3 2ln , 5af x x x g x x xx      ，若对任意的 x1，x2∈ 1 ,22      ，都有    1 2 2f x g x  成立，则 a 的取值范围是 ( ) A．(0，＋∞) B．[1，＋∞) C．(－∞，0) D．(－∞，－1] 第二部分 非选择题（共 90 分） 二、填空题：本大题共 4 小题，每小题 5 分，共 20 分.请将正确填在答题卡的 横线上. 13. 已知向量 ,a b 的夹角为 60 ， 2a  ， 1b  ，则 2a b  ____ _ ___; 14、由曲线 y= 2x ,y= 3x 围成的封闭图形面积为_____ _______; 15、已知   3 23f x x x a   a 为常数)，在 3,3 上有最小值 3，那么在 3,3 上  f x 的最大值是______ ________; 16. 定义域为 R 的函数  f x 满足  1 1f  ，且  f x 的导函数   1 2f x  ，则满足   1 2 xf x  的 x 的解集为 ． 三、解答题：本大题共 6 小题，共 70 分.解答题应写出文字说明、证明过程或演算步骤. 17.（本小题满分 10 分）已知数列 na 的前 n 项和为 2 1, 2,n nS a S n n   . （Ⅰ）求数列 na 的通项公式； （Ⅱ）若数列 1 nS       的前 n 项和为 nT ,求 nT . 18. (本题满分 12 分) 在 ABC 中，角 , ,A B C 所对的边分别为 , ,a b c ，且 2 5cos 2 5 A  ， 3AB AC   . （Ⅰ）求 ABC 的面积； （Ⅱ）若 6b c  ，求 a 的值. 19.（本小题满分 12 分）已知函数    3 0f x ax cx d a    是 R 上的奇函数，当 x＝1 时，  f x 取得极值－2. （Ⅰ）求函数  f x 的解析式； （Ⅱ）求函数  f x 的单调区间和极大值； 20．(本小题满分 12 分）如图，在四棱锥 P ABCD 中， PC ⊥底面 ABCD ， = 2AD BC AD BC ∥ ， 2 ， 2,PC  ABC 是以 AC 为斜边的等腰直角三角形， E 是 PD 的中点． （Ⅰ）求证：平面 EAC ⊥平面 PCD； （Ⅱ）求直线 PA 与平面 EAC 所成角的余弦值. 21.(本小题满分 12 分)已知椭圆 2 2: 2 4C x y  . （Ⅰ）求椭圆 C 的离心率； （Ⅱ）设 O 为原点，若点 A 在椭圆 C 上，点 B 在直线 y＝2 上，且OA OB ，试判断直 线 AB 与圆 2 2 2x y  的位置关系，并证明你的结论． 22．(本小题满分 12 分）已知函数    Raaxxaxf  3ln . （Ⅰ）求函数  xf 的单调区间； （Ⅱ）若函数  xfy  的图像在点   2,2 f 处的切线倾斜角为 45 ，对于任意的  2,1t ， 函数           2'23 mxfxxxg 在区间  3,t 上总不是单调函数，求 m 的取值范围. 2017-2018 齐市八中高二下学期第一月考数学试题参考答案及评分标准 一、选择题：本大题共 12 小题，每小题 5 分． 题 号 1 2 3 4 5 6 7 8 9 1 0 11 1 2 答 案 D D B C B B A A D D C B 二．填空题：13. 10 ； 14. 1; 15. 57; 16. {x|x<1} 三．解答题： 17．17、解：(1)在△ABC 中，cos B＝－cos(A＋C)．由已知，得(1－sin2B)－cos(A＋C)＝1 －cos Acos C，∴－sin2B－(cos Acos C－sin Asin C)＝－cos Acos C， 化简，得 sin2B＝sin Asin C．由正弦定理，得 b2＝ac，∴a，b，c 成等比数列． (2)由(1)及题设条件，得 ac＝4. 则 cos B＝ a2＋c2－b2 2ac ＝ a2＋c2－ac 2ac ≥ 2ac－ac 2ac ＝ 1 2， 当且仅当 a＝c 时，等号成立．∵0＜B＜π，∴sin B＝≤ 1 2＝ 3 2. ∴S△ABC＝ 1 2acsin B≤ 1 2×4× 3 2＝. ∴△ABC 的面积的最大值为. 18[解析] (1)∵f(x)是 R 上的奇函数，∴f(－x)＝－f(x)，即－ax3－cx＋d＝－ax3－cx－d， ∴d＝－d，∴d＝0(或由 f(0)＝0 得 d＝0)．∴f(x)＝ax3＋cx，f ′(x)＝3ax2＋c，又当 x＝1 时，f(x)取得极值－2，∴ f 1 ＝－2， f ′ 1 ＝0， 即 a＋c＝－2， 3a＋c＝0， 解得 a＝1， c＝－3. ∴f(x)＝x3 －3x. (2)f ′(x)＝3x2－3＝3(x＋1)(x－1)，令 f ′(x)＝0，得 x＝±1，当－11 时，f ′(x)>0，函数 f(x)单调递增； ∴函数 f(x)的递增区间是(－∞，－1)和(1，＋∞)；递减区间为(－1,1)． 因此，f(x)在 x＝－1 处取得极大值，且极大值为 f(－1)＝2. 19.解：解：（1）因为 ， ，所以 或 （舍去）. 又 ，故 ，所以数列 的通项公式为 . （2）由（Ⅰ）知 ，∴ ，① ∴ ，② ② ①得 ，∴ . 20. 【答案】 (1)略 (2)略 (3)8 3 21. 解：(1)由题意，椭圆 C 的标准方程为 x2 4 ＋ y2 2 ＝1.∴a2＝4，b2＝2，从而 c2＝a2－b2＝2.因 此 a＝2，c＝.故椭圆 C 的离心率 e＝ c a＝ 2 2. (2)直线 AB 与圆 x2＋y2＝2 相切．证明如下： 设点 A，B 的坐标分别为(x0，y0)，(t，2)，其中 x0≠0.∵OA⊥OB，∴ OA →· OB →＝0，即 tx0 ＋2y0＝0，解得 t＝－ 2y0 x0 . 当 x0＝t 时，y0＝－ t2 2 ，代入椭圆 C 的方程，得 t＝±， 故直线 AB 的方程为 x＝±.圆心 O 到直线 AB 的距离 d＝，此时直线 AB 与圆 x2＋y2＝2 相 切． 当 x0≠t 时，直线 AB 的方程为 y－2＝ y0－2 x0－t(x－t)，即(y0－2)x－(x0－t)y＋2x0－ty0＝0， 圆心 O 到直线 AB 的距离 d＝ |2x0－ty0| （y0－2）2＋（x0－t）2 .又 x 2 0＋2y 2 0＝4，t＝－ 2y0 x0 ，故 d＝ = ＝，此时直线 AB 与圆 x2＋y2＝2 22．解： （1）     01' >xx xaxf  ， 当 0>a 时，  xf 的单调递增区间为  1,0 ，单调递减区间为  ,1 ； 当 0 < g tg 由题意知：对于任意的     0',2,1 < < g g g ∴ ,93 37  << m ∴ m 的取值范围为 .9,3 37      