江西省宜春市靖安中学2019-2020学年高一上学期月考数学试题 18页

www.ks5u.com ‎2019-2020学年度上学期高一年级第二次月考数学试卷 一、选择题 ‎1.若幂函数在上是递减函数，则的值为（ ）‎ A. -1 B. -3 C. 1 D. 3‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据函数f（x）是幂函数列方程m2﹣2m﹣2＝1求得m的值，再讨论是否满足f（x）是（0，+∞）上的减函数．‎ ‎【详解】函数f（x）＝（m2﹣2m﹣2）xm-2是幂函数，‎ 则m2﹣2m﹣2＝1，即m2﹣2m﹣3＝0，‎ 解得m＝3或m＝﹣1；‎ 当m＝3时， m﹣2＝1，函数f（x）＝x不是（0，+∞）上的减函数，不满足题意；‎ 当m＝﹣1时，m﹣2＝-3，函数f（x）＝是（0，+∞）上的减函数，满足题意；‎ 所以m的值为-1．‎ 故选：A ‎【点睛】本题考查了幂函数的定义与性质的应用问题，是基础题．‎ ‎2.一个平面四边形的斜二测画法的直观图是一个边长为的正方形，则原平面四边形的面积等于（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ 试题分析：根据斜二测画法画平面图形的直观图的规则，可以得出一个平面图形的面积S与它的直观图的面积S′之间的关系是S′=S，本题中直观图的面积为，所以原平面四边形的面积等于．‎ 考点：平面图形的直观图 ‎3.与函数的图象相同的函数是 （ ）‎ A. B. C. D. 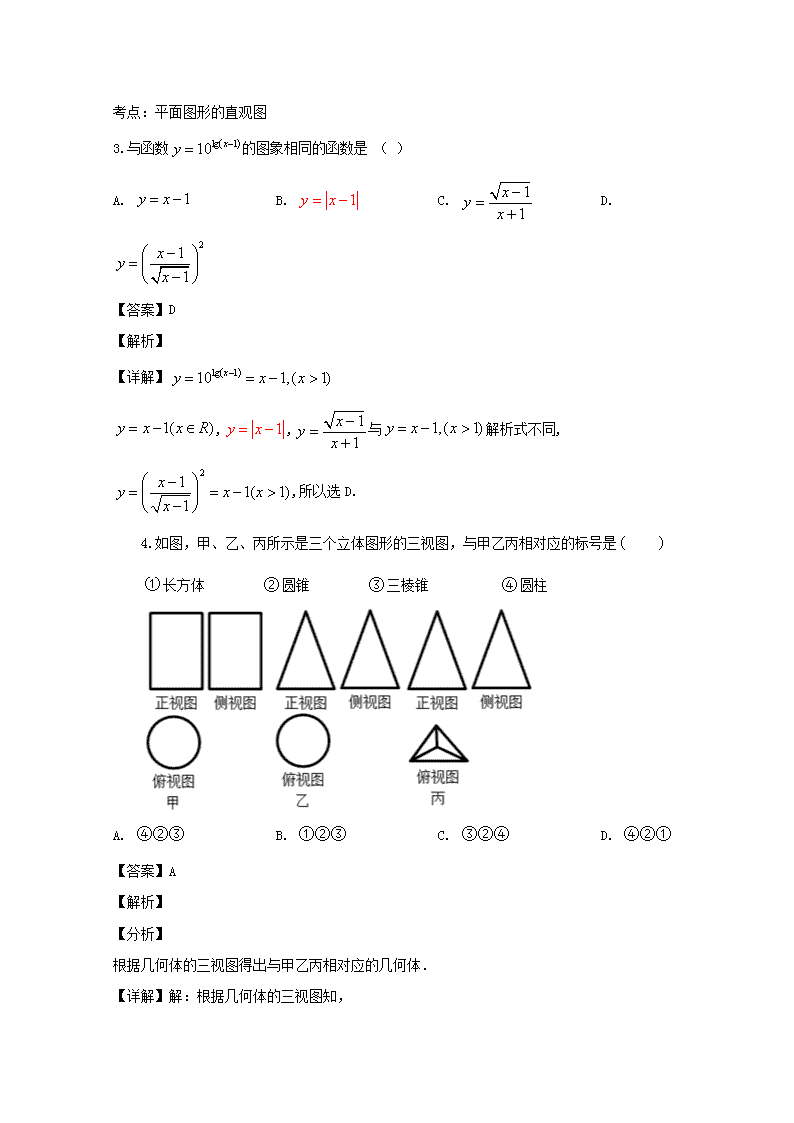‎ ‎【答案】D ‎【解析】‎ ‎【详解】‎ ‎,,与解析式不同,‎ ‎,所以选D.‎ ‎4.如图，甲、乙、丙所示是三个立体图形的三视图，与甲乙丙相对应的标号是　　‎ 长方体    圆锥    三棱锥     圆柱 A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据几何体的三视图得出与甲乙丙相对应的几何体．‎ ‎【详解】解：根据几何体的三视图知，‎ 甲是圆柱，乙是圆锥，丙是三棱锥；‎ 则甲乙丙对应的序号是．‎ 故选A．‎ ‎【点睛】本题考查了根据几何体的三视图判断几何体结构特征的应用问题，是基础题．‎ ‎5.已知，，则的值为（ ）‎ A. 3 B. 17 C. -10 D. -24‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 记，根据为奇函数，即为奇函数，结合即可得出的值.‎ ‎【详解】记，则.‎ 又因为，即.‎ 所以.‎ 所以 故选:D.‎ ‎【点睛】本题考查根据奇函数的性质求对称点的函数值.将非奇函数变成奇函数，是解本题的关键.属于中档题.‎ ‎6.下列条件中，可判定平面与平面平行的是（ ）‎ A. 、都垂直于平面 B. 、是两条异面直线，且，且 C. 内不共线的三个点到的距离相等 D. 、是内两条直线，且 ‎【答案】B ‎【解析】‎ ‎【分析】‎ 根据面面平行的判定定理与性质定理即可得出答案.‎ ‎【详解】A.如图所示：‎ ‎ ‎ 平面与平面不平行，错误.‎ B.在过直线的平面上取直线，且.‎ 因为、是两条异面直线，则直线与直线相交,记此平面为,‎ 因为，，即且,‎ 所以.‎ 因为，，即且,‎ 所以.‎ 所以.正确.‎ C.如图所示：‎ ‎ 内不共线的三个点到的距离相等,但平面与平面不平行，错误.‎ D.如图所示：‎ ‎、是内两条直线，且.但平面与平面不平行，错误.‎ 故选：B.‎ ‎【点睛】本题考查面面平行的判定定理与性质定理，熟练掌握面面平行的判定与性质定理是解本题的关键.属于基础题.‎ ‎7.设实数满足则的大小关系为 A. c