- 464.50 KB
- 2021-04-21 发布
1.已知一个几何体的三视图如图5所示,则这个几何体的体积是( )
A. B. C. D.
【答案】 D
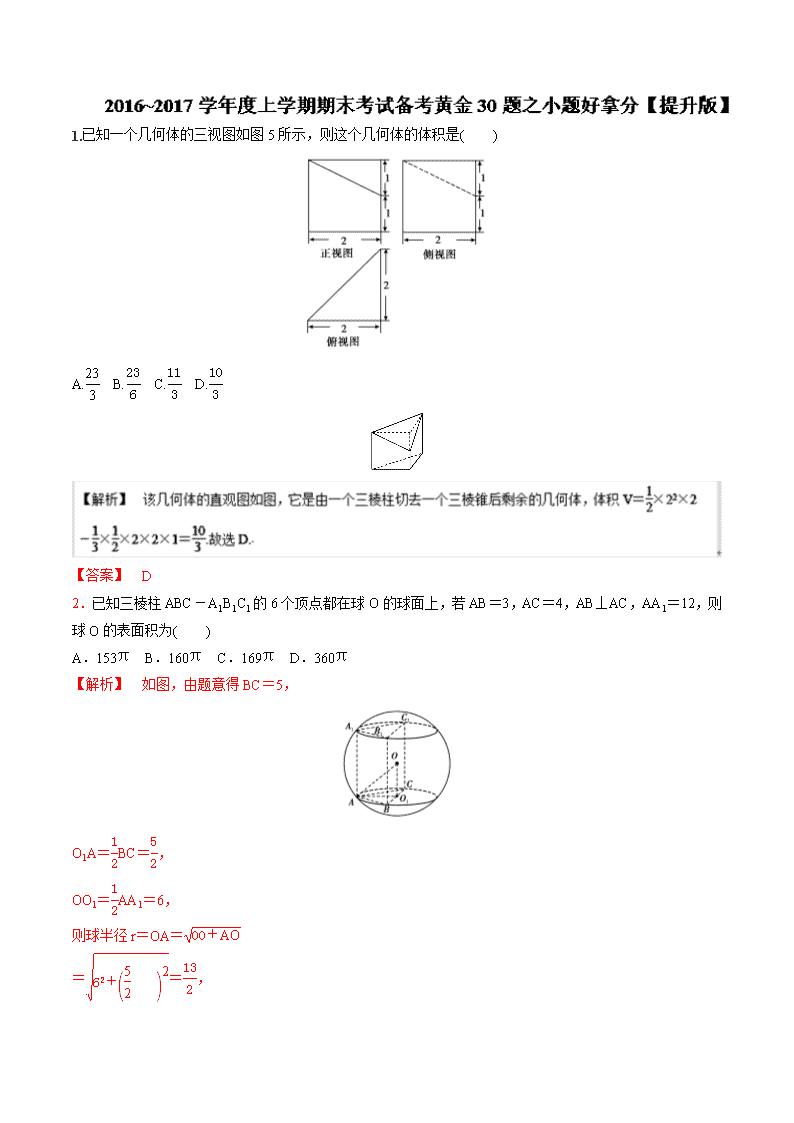
2.已知三棱柱ABC-A1B1C1的6个顶点都在球O的球面上,若AB=3,AC=4,AB⊥AC,AA1=12,则球O的表面积为( )
A.153π B.160π C.169π D.360π
【解析】 如图,由题意得BC=5,
O1A=BC=,
OO1=AA1=6,
则球半径r=OA=
==,
S球=4πr2=169π.故选C.
【答案】 C
3.在正方体ABCD-A1B1C1D1中,异面直线AA1与BC1所成的角为( )
A.60° B.45°
C.30° D.90°
【解析】 因为AA1∥BB1,
所以∠B1BC1是AA1与BC1所成的角,∠B1BC1=45°.
【答案】 B
4.已知三棱柱ABC—A1B1C1的侧棱与底面垂直,体积为,底面是边长为的正三角形.若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为( )
A. B. C. D.
【解析】
【答案】 B
5.若A(-2,3),B(3,-2),C三点共线,则m的值为( )
A.-2 B.- C. D.2
【解析】 因为A、B、C三点共线,则kAB=kAC,
即=,解得m=.
【答案】 C
6.已知点A(0,2),B(2,0).若点C在函数y=x2的图象上,则使得△ABC的面积为2的点C的个数为( )
A.4 B.3 C.2 D.1
【答案】 A
7.圆x2+y2-2x-2y+1=0上的点到直线x-y=2的距离最大值是( )
A.2 B.1+
C.1+ D.1+2
【解析】 由圆的方程可得圆心坐标为(1,1),半径为1,则圆心到直线x-y=2的距离为d==,则圆上的点到直线x-y=2的最大距离为+1.
【答案】 B
8.已知圆x2+y2+2x-2y+a=0截直线x+y+2=0所得弦的长度为4,则实数a的值是( )
A.-2 B.-4 C.-6 D.-8
【解析】 圆的标准方程为(x+1)2+(y-1)2=2-a,圆心C(-1,1),半径r满足r2=2-a,则圆心C到直线x+y+2=0的距离d==,所以r2=4+2=2-a⇒a=-4.
【答案】 B
9.命题“所有能被2整除的整数都是偶数”的否定是( )
A.所有不能被2整除的整数都是偶数
B.所有能被2整除的整数都不是偶数
C.存在一个不能被2整除的整数是偶数
D.存在一个能被2整除的整数不是偶数
【解析】 把全称量词改为存在量词并把结论否定.
【答案】 D
10.对∀x∈R,kx2-kx-1<0是真命题,则k的取值范围是( )
A.-4≤k≤0 B.-4≤k<0
C.-4<k≤0 D.-4<k<0
【答案】 C
11.已知命题p:∀x>0,总有(x+1)ex>1,则p为( )
A.∃x0≤0,使得(x0+1)ex0≤1
B.∃x0>0,使得(x0+1)ex0≤1
C.∀x>0,总有(x+1)ex≤1
D.∀x≤0,使得(x+1)ex≤1
【解析】 因为全称命题∀x∈M,p(x)的否定为∃x0∈M,p(x),故p:∃x0>0,使得(x0+1)ex0≤1.
【答案】 B
12.抛物线y2=4x的焦点到双曲线x2-=1的渐近线的距离是( )
A. B.
C.1 D.
【解析】 抛物线y2=4x的焦点为(1,0),到双曲线x2-=1的渐近线x-y=0的距离为=,故选B.
【答案】 B
13.已知椭圆C:+y2=1的右焦点为F,直线l:x=2,点A∈l,线段AF交椭圆C于点B,若=3,则|
eq o(AF,sup6(→))|=( )
A. B.2
C. D.3
【答案】 A
14.若点O和点F(-2,0)分别为双曲线-y2=1(a>0)的中心和左焦点,点P为双曲线右支上的任意一点,则·的取值范围为( )
A.3-2,+∞) B.3+2,+∞)
C. D.
【解析】 因为双曲线左焦点的坐标为F(-2,0),
所以c=2.
所以c2=a2+b2=a2+1,
即4=a2+1,解得a=.
设P(x,y),则·=x(x+2)+y2,
因为点P在双曲线-y2=1上,
所以·=x2+2x-1=--1.
又因为点P在双曲线的右支上,所以x≥.
所以当x=时,·最小,且为3+2,
即·的取值范围是3+2,+∞).
【答案】 B
15.已知直线y=k(x+2)与双曲线-=1,有如下信息:联立方程组消去y后得到方程Ax2+Bx+C=0,分类讨论:(1)当A=0时,该方程恒有一解;(2)当A≠0时,Δ=B2-4AC≥0恒成立.在满足所提供信息的前提下,双曲线离心率的取值范围是( )
A.(1, ] B.,+∞)
C.(1,2] D.2,+∞)
【解析】 依题意可知直线恒过定点(-2,0),根据(1)和(2)可知直线与双曲线恒有交点,故需要定点(-2,0)在双曲线的左顶点上或左顶点的左边,即-2≤-,即00)上的一点,F为抛物线的焦点,直线l过点P且与x轴平行,若同时与直线l、直线PF、x轴相切且位于直线PF左侧的圆与x轴切于点Q,则点Q( )
A.位于原点的左侧 B.与原点重合
C.位于原点的右侧 D.以上均有可能
【答案】 B
17.若F1,F2为双曲线C:-y2=1的左、右焦点,点P在双曲线C上,∠F1PF2=60°,则点P到x轴的距离为( )
A. B.
C. D.
【答案】 B
18.已知向量a,b是平面α内的两个不相等的非零向量,非零向量c在直线l上,则“c·a=0,且c·b=0”是l⊥α的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【解析】 若l⊥α,则l垂直于α内的所有直线,从而有c·a=0,c·b=0.反之,由于a,b是否共线没有确定,若共线,则结论不成立;若不共线,则结论成立.
【答案】 B
19.已知正四棱柱ABCDA1B1C1D1中,AA1=2AB,则CD与平面BDC1所成角的正弦值等于( )
A. B.
C. D.
【解析】 以D为坐标原点,建立空间直角坐标系,如图,设AA1=2AB=2,则D(0,0,0),C(0,1,0),B(1,1,0),C1(0, 1,2),则=(0,1,0),= (1,1,0),=(0,1,2).设平面BDC1的法向量为n=(x,y,z),则n⊥,n⊥,所以有令y=-2,得平面BDC1的一个法向量为n=(2,-2,1).设CD与平面BDC1所成的角为θ,则sin θ=|cos〈n,〉|==.
【答案】 A
20.已知正方体ABCDA1B1C1D1中,若点F是侧面CD1的中心,且=+m-n,则m,n的值分别为( )
A.,- B.-,-
C.-, D.,
【解析】 由于=+=+(+)=++,所以m=,n=-,故选A.
【答案】 A
21.在矩形ABCD中,AB=3,AD=4,PA⊥平面ABCD,PA=,那么二面角ABDP的大小为( )
A.30° B.45°
C.60° D.75°
又n1=为平面ABCD的一个法向量,
∴cos〈n1,n〉==.∴所求二面角为30°.
【答案】 A
22.如图所示,斜二测画法得到直观图四边形A′B′C′D′是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是________.
【解析】 在梯形A′B′C′D′中,B′C′=A′D′+2·A′B′cos45°=1+,则原平面图形是上底为1,下底为1+,高为2的直角梯形,其面积S=(1+1+)×2=2+.
【答案】 2+
23.如图,正方形ABCD的边长为a,沿对角线AC将△ADC折起,若∠DAB=60°
,则二面角D-AC-B的大小为________.
【答案】 90°
24.已知a,b,c表示直线,α表示平面,给出下列四个命题:
①若a∥α,b∥α,则a∥b;
②若b⊂α,a∥b,则a∥α;
③若a⊥c,b⊥c,则a∥b;
④若a⊥α,b⊥α,则a∥b.
正确命题的序号是________.
【解析】 当a∥α,b∥α时,a与b的关系不确定,即①不正确;当b⊂α,a∥b时,a也可能在α内,即②不正确;当a⊥c,b⊥c时,a与b的关系不确定,即③不正确;由线面垂直的性质定理知④正确.
【答案】 ④
25.已知点A(x,5)关于点C(1,y)的对称点是B(-2,-3),则点P(x,y)到原点的距离是________.
【解析】 由已知得⇒
则P点坐标为(4,1),P到原点的距离为d==.
【答案】
26.已知直线l:x+y-2=0和圆C:x2+y2-12x-12y+54=0,则与直线l和圆C都相切且半径最小的圆的标准方程是________.
【答案】 (x-2)2+(y-2)2=2
27.给出以下判断:
①命题“负数的平方是正数”不是全称命题;
②命题“∀x∈N,x3>x2”的否定是“∃x0∈N,使x>x”;
③“b=0”是“函数f(x)=ax2+bx+c为偶函数”的充要条件;
④“正四棱锥的底面是正方形”的逆命题为真命题.
其中正确命题的序号是________.
【解析】 ①②④是假命题,③是真命题.
【答案】③
28.设F为抛物线C:y2=4x的焦点,过点P(-1,0)的直线l交抛物线C于A,B两点,点Q为线段AB的中点,若|PQ|=2,则直线l的斜率等于________.
【解析】 设直线l的方程为
y=k(x+1),A(x1,y1),B(x2,y2).
【答案】 ±1
29.已知抛物线y2=4x的焦点为F,若点A,B是该抛物线上的点,∠AFB=,线段AB的中点M在抛物线的准线上的射影为N,则的最大值为______.
【解析】 如图所示,设|AF|=a,|BF|=b,则|AB|=,而根据抛物线的定义可得|MN|=,又≤,所以=≤,当且仅当a=b时,等号成立,即的最大值为.
【答案】
30.如图,在四棱锥SABCD中,底面ABCD是边长为1的正方形,S到A,B,C,D的距离都等于2.
给出以下结论:①+++=0;②+--=0;③-+-=0;④·=·;⑤·=0,其中正确结论的序号是________.
【答案】③④