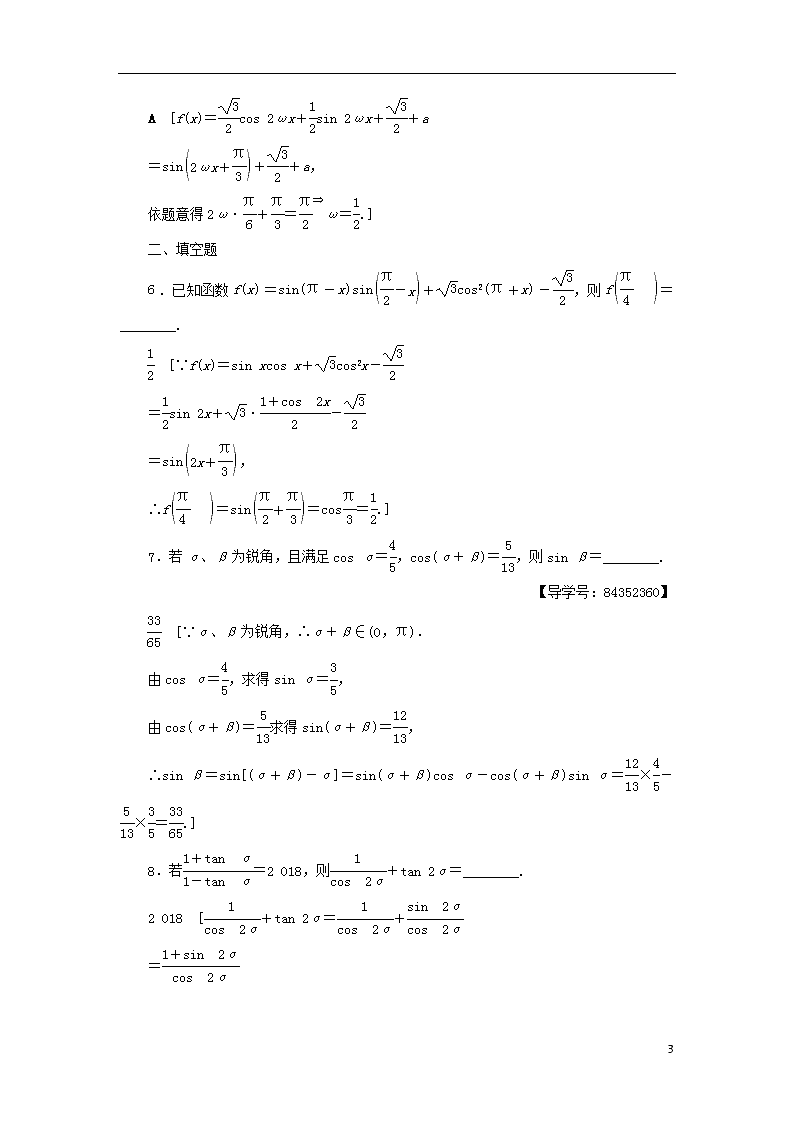- 85.00 KB
- 2021-04-21 发布
专题强化训练(四)
(建议用时:45分钟)
[学业达标练]
一、选择题
1.cos 555°的值为( )
【导学号:84352357】
A. B.-
C. D.
B [cos 555°=cos(360°+180°+15°)
=-cos 15°
=-cos(45°-30°)
=-
=-.]
2.sin αcos(α+30°)-cos αsin(α+30°)等于( )
A.- B.
C.- D.
A [sin αcos(α+30°)-cos αsin(α+30°)=sin[α-(α+30°)]=sin(-30°)=-sin 30°=-.]
3.已知α,β∈,sin α=,cos β=,则α-β等于( )
【导学号:84352358】
A.- B.
C. D.-或
A [∵α∈,sin α=,
∴cos α=,
∵β∈,cos β=,
7
∴sin β=,
∴sin(α-β)=sin αcos β-cos αsin β
=×-×=-,
又α-β∈,∴α-β=-.]
4.函数y=cos2+sin2-1是( )
A.最小正周期为2π的奇函数
B.最小正周期为π的偶函数
C.最小正周期为π的奇函数
D.最小正周期为2π的偶函数
C [y=+-1
=cos-cos
=
=sin 2x,
∴f(x)是最小正周期为π的奇函数.]
5.设函数f(x)=cos2ωx+sin ωxcos ωx+a(其中ω>0,a∈R).且f(x)的图象在y轴右侧的第一个最高点的横坐标是,则ω的值为( )
【导学号:84352359】
A. B.-
C.- D.
A [f(x)=cos 2ωx+sin 2ωx++a
=sin++a,
7
依题意得2ω·+=⇒ω=.]
二、填空题
6.已知函数f(x)=sin(π-x)sin+cos2(π+x)-,则f=________.
[∵f(x)=sin xcos x+cos2x-
=sin 2x+·-
=sin,
∴f=sin=cos=.]
7.若α、β为锐角,且满足cos α=,cos(α+β)=,则sin β=________.
【导学号:84352360】
[∵α、β为锐角,∴α+β∈(0,π).
由cos α=,求得sin α=,
由cos(α+β)=求得sin(α+β)=,
∴sin β=sin[(α+β)-α]=sin(α+β)cos α-cos(α+β)sin α=×-×=.]
8.若=2 018,则+tan 2α=________.
2 018 [+tan 2α=+
=
==
==2 018.]
三、解答题
9.已知α∈,sin α=.
7
(1)求sin的值;
(2)求cos的值.
【导学号:84352361】
[解] (1)因为α∈,sin α=,
所以cos α=-=-.
故sin=sincos α+cossin α
=×+×=-.
(2)由(1)知sin 2α=2sin αcos α=2××=-,
cos 2α=1-2sin2α=1-2×2=,
所以cos=coscos 2α+sinsin 2α
=×+×
=-.
10.已知函数f(x)=sin x·(2cos x-sin x)+cos2x.
(1)求函数f(x)的最小正周期;
(2)若<α<,且f(α)=-,求sin 2α的值.
[解] (1)因为f(x)=sin x·(2cos x-sin x)+cos2x,
所以f(x)=sin 2x-sin2x+cos2x
=sin 2x+cos 2x=sin,
所以函数f(x)的最小正周期是π.
(2)f(α)=-,即sin=-,
sin=-.
因为<α<,所以<2α+<,
7
所以cos=-,
所以sin 2α=sin
=sin-cos=×-×=.
[冲A挑战练]
1.若(4tan α+1)(1-4tan β)=17,则tan(α-β)等于( )
A.2 B.3
C.4 D.5
C [由已知得,4(tan α-tan β)=16(1+tan αtan β),
即=4,
∴tan(α-β)=4.]
2.在△ABC中,若B=45°,则cos Asin C的取值范围是( )
【导学号:84352362】
A.[-1,1] B.
C. D.
B [∵B=45°,∴A+C=135°,C=135°-A,
∴cos Asin C=cos Asin(135°-A)
=cos A·
=cos2A+sin Acos A
=·+·
=(sin 2A+cos 2A+1)
=[sin(2A+45°)+1]
=sin(2A+45°)+,
∵0°<A<135°,
∴45°<2A+45°<315°,
7
∴-1≤sin(2A+45°)≤1,
∴cos Asin C∈.]
3.已知向量a=(4,5cos α),b=(3,-4tan α),α∈,若a⊥b,则cos=________.
- [因为a⊥b,所以4×3+5cos α×(-4tan α)=0,
解得sin α=.
又因为α∈,所以cos α=.
cos 2α=1-2sin2α=,sin 2α=2sin αcos α=,
于是cos=cos 2αcos-sin 2αsin
=-.]
4.函数f(x)=的值域为________.
[f(x)==
=2sin x(1+sin x)
=22-,
由1-sin x≠0得-1≤sin x<1,
所以f(x)=的值域为.]
5.已知函数f(x)=a(cos2x+sin xcos x)+b.
(1)当a>0时,求f(x)的单调递增区间;
(2)当a<0且x∈时,f(x)的值域是[3,4],求a,b的值.
【导学号:84352363】
[解] f(x)=a·+a·sin 2x+b
=sin++b.
(1)2kπ-≤2x+≤2kπ+,k∈Z,kπ-≤x≤kπ+(k∈Z),即x∈,k
7
∈Z,
故f(x)的单调递增区间为,k∈Z.
(2)0≤x≤,≤2x+≤,
-≤sin≤1,
f(x)min=a+b=3,f(x)max=b=4,
∴a=2-2,b=4.
7
相关文档
- 2019_2020学年高中语文第三课神奇2021-04-21 15:53:4511页
- 高中生物第三章细胞的基本结构3_32021-04-21 15:53:083页
- 语文卷·2019届广西河池高中高二上2021-04-21 15:52:4312页
- 2020高中数学 模块综合测评 新人教2021-04-21 15:52:1210页
- 高中数学(人教A版)必修4:1-2-1-2同步2021-04-21 15:51:525页
- 2020_2021学年高中历史第六单元现2021-04-21 15:51:4511页
- 2019-2020学年同步人教版高中历史2021-04-21 15:47:573页
- 2019-2020学年高中生物人教版必修2021-04-21 15:46:228页
- 国旗下讲话稿之国旗下讲话-高中生2021-04-21 15:46:223页
- 高中新教师工作心得体会合集5篇2021-04-21 15:43:0712页