【物理】2018届一轮复习人教版牛顿运动定律的综合应用教案 7页

第12讲 牛顿运动定律的综合应用 ‎【教学目标】‎ ‎1.掌握超重、失重的概念，会分析有关超重、失重的问题.‎ ‎2.学会分析临界与极值问题.‎ ‎3.会进行动力学多过程问题的分析．‎ ‎【教学过程】 ‎ ‎★重难点一、对超重、失重的理解★‎ 一、　对超重、失重的理解 ‎(1)不论超重、失重或完全失重，物体的重力都不变，只是“视重”改变。‎ ‎(2)物体是否处于超重或失重状态，不在于物体向上运动还是向下运动，而在于物体具有向上的加速度还是向下的加速度，这也是判断物体超重或失重的根本所在。‎ ‎(3)当物体处于完全失重状态时，重力只有使物体产生a＝g的加速度效果，不再有其他效果。此时，平常一切由重力产生的物理现象都会完全消失，如单摆停摆、天平失效、液体不再产生压强和浮力等。‎ ‎【特别提醒】‎ 超重和失重现象的判断“三”角度 ‎1．从受力的角度判断，当物体所受向上的拉力(或支持力)大于重力时，物体处于超重状态，小于重力时处于失重状态，等于零时处于完全失重状态。‎ ‎2．从加速度的角度判断，当物体具有向上的加速度时处于超重状态，具有向下的加速度时处于失重状态，向下的加速度为重力加速度时处于完全失重状态。‎ ‎3．从速度变化角度判断 ‎(1)物体向上加速或向下减速时，超重；‎ ‎(2)物体向下加速或向上减速时，失重。‎ ‎【典型例题】据某网站消息，安徽凤阳县7岁“大力士”杨金龙名声鹊起后，南京、天津等地诸多体育专业学校纷纷向他抛出橄榄枝。最终，在安徽省举重队推荐下小金龙选择了铜陵市业余体校举重队，教练盛红星称，在省队测试的时候，小金龙不仅举起45 kg杠铃，还背起体重高达120 kg的王军教练，简直能“秒杀同龄的施瓦辛格”，g＝10 m/s2，请计算 ‎(1)在以a＝2 m/s2匀加速下降的电梯中小金龙能举起杠铃的质量是多少？‎ ‎(2)在以a＝2 m/s2匀加速上升的电梯中小金龙能背起的质量又是多少？‎ ‎【答案】　(1)56.25 kg　(2)100 kg ‎【解析】　(1)小金龙的举力是一定的，则有F1＝mg＝450 N 在以a＝2 m/s2匀加速下降的电梯中，设其能举起杠铃的质量为m1，则有m1g－F1＝m1a 解得m1＝56.25 kg ‎(2)小金龙能背起的重量是一定的，则有F2＝Mg＝1 200 N 在以a＝2 m/s2匀加速上升的电梯中，设其能背起的质量为m2，‎ 则有F2－m2g＝m2a 解得m2＝100 kg。‎ ‎★重难点二、动力学中整体法与隔离法的应用★‎ 整体法与隔离法在动力学问题中的应用 ‎1．整体法的选取原则 若连接体内各物体具有相同的加速度，且不需要求物体之间的作用力，可以把它们看成一个整体，分析整体受到的合外力，应用牛顿第二定律求出加速度(或其他未知量)。‎ ‎2．隔离法的选取原则 若连接体内各物体的加速度不相同，或者要求出系统内各物体之间的作用力时，就需要把物体从系统中隔离出来，应用牛顿第二定律列方程求解。‎ ‎3．整体法、隔离法的交替运用 若连接体内各物体具有相同的加速度，且要求物体之间的作用力时，可以先用整体法求出加速度，然后再用隔离法选取合适的研究对象，应用牛顿第二定律求作用力，即“先整体求加速度，后隔离求内力”。‎ ‎4．整体法与隔离法常涉及的三种问题类型 ‎(1)涉及滑轮的问题：若要求绳的拉力，一般都采用隔离法。‎ ‎(2)水平面上的连接体问题：‎ ‎①这类问题一般是连接体(系统)各物体保持相对静止，即具有相同的加速度。解题时，一般采用先整体后隔离的方法，‎ ‎②建立直角坐标系时要考虑矢量正交分解越少越好的原则，或者正交分解力，或者正交分解加速度。‎ ‎(3)斜面体与物体组成的连接体问题：当物体具有沿斜面方向的加速度，而斜面体相对于地面静止时，一般采用隔离法分析。‎ ‎5．解题思路 物体系的动力学问题涉及多个物体的运动，各物体既相互独立，又通过内力相互联系。处理各物体加速度都相同的连接体问题时，整体法与隔离法往往交叉使用，一般思路是：‎ ‎(1)求内力时，先用整体法求加速度，再用隔离法求物体间的作用力。‎ ‎(2)求外力时，先用隔离法求加速度，再用整体法求整体受到的外加作用力。‎ ‎【特别提醒】‎ 正确地选取研究对象是解题的首要环节，弄清各物体之间哪些属于连接体，哪些物体应该单独分析，并分别确定出它们的加速度，然后根据牛顿运动定律列方程求解。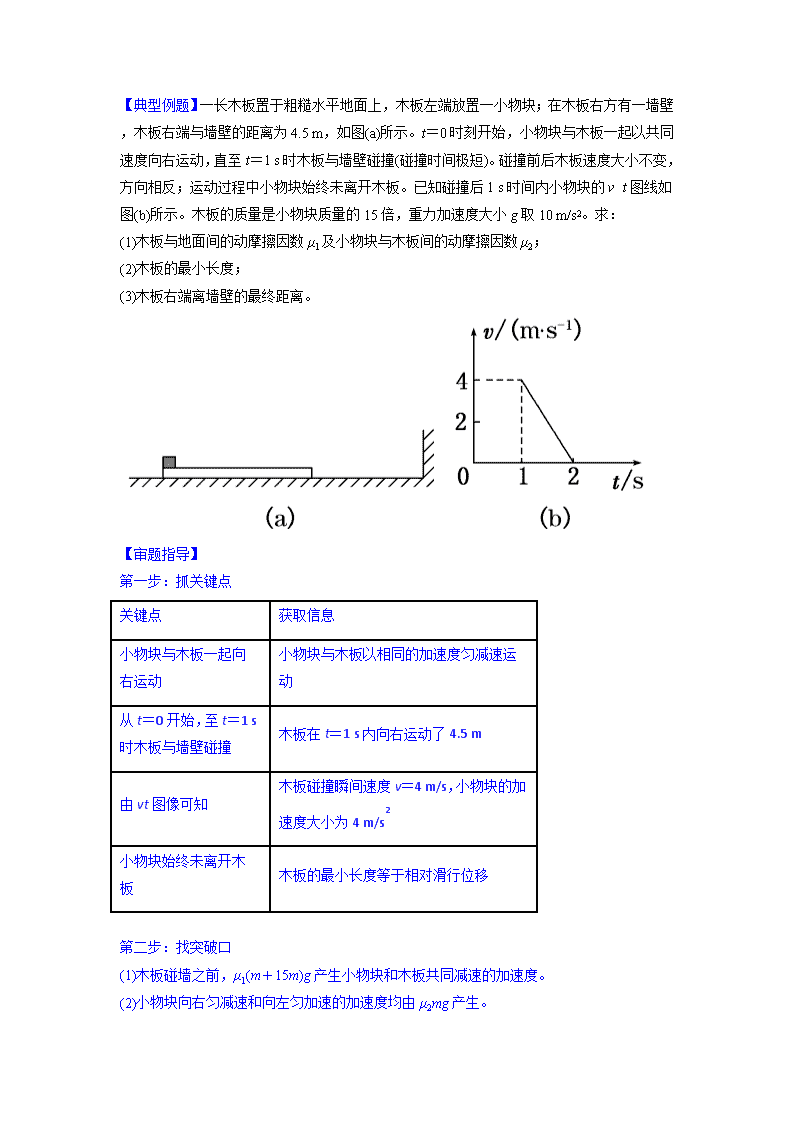‎ ‎【典型例题】一长木板置于粗糙水平地面上，木板左端放置一小物块；在木板右方有一墙壁，木板右端与墙壁的距离为4.5 m，如图(a)所示。t＝0时刻开始，小物块与木板一起以共同速度向右运动，直至t＝1 s时木板与墙壁碰撞(碰撞时间极短)。碰撞前后木板速度大小不变，方向相反；运动过程中小物块始终未离开木板。已知碰撞后1 s时间内小物块的v t图线如图(b)所示。木板的质量是小物块质量的15倍，重力加速度大小g取10 m/s2。求：‎ ‎(1)木板与地面间的动摩擦因数μ1及小物块与木板间的动摩擦因数μ2；‎ ‎(2)木板的最小长度；‎ ‎(3)木板右端离墙壁的最终距离。‎ ‎【审题指导】‎ 第一步：抓关键点 关键点 获取信息 小物块与木板一起向右运动 小物块与木板以相同的加速度匀减速运动 从t＝0开始，至t＝1 s时木板与墙壁碰撞 木板在t＝1 s内向右运动了4.5 m 由vt图像可知 木板碰撞瞬间速度v＝4 m/s，小物块的加速度大小为4 m/s2‎ 小物块始终未离开木板 木板的最小长度等于相对滑行位移 第二步：找突破口 ‎(1)木板碰墙之前，μ1(m＋15m)g产生小物块和木板共同减速的加速度。‎ ‎(2)小物块向右匀减速和向左匀加速的加速度均由μ2mg产生。‎ ‎(3)小物块相对于木板滑行过程中，木板受地面的滑动摩擦力和小物块的滑动摩擦力方向均水平向右。‎ ‎(4)小物块与木板相对静止后将一起向左做匀减速运动，而不再发生相对滑动。‎ ‎【答案】　(1)0.1　0.4　 (2)6.0 m　(3)6.5 m ‎【解析】　(1)规定向右为正方向。木板与墙壁相碰前，小物块和木板一起向右做匀变速运动，设加速度为a1，小物块和木板的质量分别为m和M。对小物块与木板整体由牛顿第二定律得 ‎－μ1(m＋M)g＝(m＋M)a1 ①‎ 由题图(b)可知，木板与墙壁碰撞前瞬间的速度v1＝4 m/s，由运动学公式有 v1＝v0＋a1t1 ②‎ x0＝v0t1＋a1t12 ③‎ 式中，t1＝1 s，x0＝4.5 m是木板碰撞前的位移，v0是小物块和木板开始运动时的速度。‎ 联立①②③式和题给条件得 μ1＝0.1 ④‎ 在木板与墙壁碰撞后，木板以－v1的初速度向左做匀变速运动，小物块以v1的初速度向右做匀变速运动。设小物块的加速度为a2，由牛顿第二定律有 ‎－μ2mg＝ma2 ⑤‎ 由题图(b)可得 a2＝ ⑥‎ 式中，t2＝2 s，v2＝0，联立⑤⑥式和题给条件得 μ2＝0.4。 ⑦‎ ‎(2)设碰撞后木板的加速度为a3，经过时间Δt，木板和小物块刚好具有共同速度v3。由牛顿第二定律及运动学公式得 μ2mg＋μ1(M＋m)g＝Ma3 ⑧‎ v3＝－v1＋a3Δt ⑨‎ v3＝v1＋a2Δt ⑩‎ 碰撞后至木板和小物块刚好达到共同速度的过程中，木板运动的位移为 x1＝Δt ⑪‎ 小物块运动的位移为 x2＝Δt ⑫‎ 小物块相对木板的位移为 Δx＝x2－x1 ⑬‎ 联立⑥⑧⑨⑩⑪⑫⑬式，并代入数值得 Δx＝6.0 m ⑭‎ 因为运动过程中小物块没有脱离木板，所以木板的最小长度应为6.0 m。‎ ‎(3)在小物块和木板具有共同速度后，两者向左做匀变速运动直至停止，设加速度为a4，此过程中小物块和木板运动的位移为x3。由牛顿第二定律及运动学公式得 μ1(m＋M)g＝(m＋M)a4 ⑮‎ ‎0－v32＝2a4x3 ⑯‎ 碰后木板运动的位移为 x＝x1＋x3 ⑰‎ 联立⑥⑧⑨⑩⑪⑮⑯⑰式，并代入数值得 x＝－6.5 m ⑱‎ 木板右端离墙壁的最终距离为6.5 m。‎ ‎★重难点三、动力学中的临界、极值问题★‎ 动力学中的临界、极值问题 ‎1．临界或极值条件的标志 ‎(1)有些题目中有“刚好”、“恰好”、“正好”等字眼，明显表明题述的过程存在着临界点。‎ ‎(2)若题目中有“取值范围”、“多长时间”、“多大距离”等词语，表明题述的过程存在着“起止点”，而这些起止点往往就对应临界状态。‎ ‎(3)若题目中有“最大”、“最小”、“至多”、“至少”等字眼，表明题述的过程存在着极值，这个极值点往往是临界点。‎ ‎(4)若题目要求“最终加速度”、“稳定加速度”等，即是求收尾加速度或收尾速度。‎ ‎2．产生临界问题的条件 接触与脱离的临界条件 两物体相接触或脱离，临界条件是：弹力FN＝0‎ 相对滑动的临界条件 两物体相接触且处于相对静止时，常存在着静摩擦力，则相对滑动的临界条件是：静摩擦力达到最大值 绳子断裂与松弛的临界条件 绳子所能承受的张力是有限的，绳子断与不断的临界条件是绳中张力等于它所能承受的最大张力，绳子松弛的临界条件是FT＝0‎ 加速度最大与速度最大的临界条件 当物体在受到变化的外力作用下运动时，其加速度和速度都会不断变化，当所受合外力最大时，具有最大加速度；合外力最小时，具有最小加速度。当出现速度有最大值或最小值的临界条件时，物体处于临界状态，所对应的速度便会出现最大值或最小值 ‎3.解决动力学临界、极值问题的常用方法 方法一　极限分析法 把物理问题(或过程)推向极端，从而使临界现象(或状态)暴露出来，以达到正确解决问题的目的。‎ 方法二　假设分析法 临界问题存在多种可能，特别是非此即彼两种可能时，或变化过程中可能出现临界条件，也可能不出现临界条件时，往往用假设法解决问题。‎ 方法三　数学极值法 将物理过程通过数学公式表达出来，根据数学表达式解出临界条件。‎ ‎【典型例题】如图所示，一质量m＝0.4 kg的小物块，以v0＝2 m/s的初速度，在与斜面某一夹角的拉力F作用下，沿斜面向上做匀加速运动，经t＝2 s的时间物块由A点运动到B点，A、B之间的距离L＝10 m。已知斜面倾角θ＝30°，物块与斜面之间的动摩擦因数μ＝。重力加速度g取10 m/s2。‎ ‎(1)求物块加速度的大小及到达B点时速度的大小；‎ ‎(2)拉力F与斜面夹角多大时，拉力F最小？拉力F的最小值是多少？‎ ‎【审题探究】‎ ‎①从A到B，做什么运动？满足什么规律？‎ ‎②拉力F的大小与F和斜面夹角α的关系式是怎样的？‎ ‎【答案】(1)3 m/s2　8 m/s　(2)30°　 N ‎【解析】　(1)设物块加速度的大小为a，到达B点时速度的大小为v，由运动学公式得 L＝v0t＋at2①‎ v＝v0＋at②‎ 联立①②式，代入数据得 a＝3 m/s2③‎ v＝8 m/s④‎ ‎(2)设物块所受支持力为FN，所受摩擦力为Ff，拉力与斜面间的夹角为α，受力分析如图所示 由牛顿第二定律得 Fcos α－mgsin θ－Ff＝ma⑤‎ Fsin α＋FN－mgcos θ＝0⑥‎ 又Ff＝μFN⑦‎ 联立⑤⑥⑦式得 F＝⑧‎ 由数学知识得 cosα＋sin α＝sin (60°＋α)⑨‎ 由⑧⑨式可知对应F最小时与斜面间的夹角 α＝30°⑩‎ 联立③⑧⑩式，代入数据得F的最小值为 Fmin＝ N。‎